Threesology Research Journal

Threesology Research Journal Persistent Dichotomies... revisited
A Study of the Threes Phenomena

Viewers as of 3/30/2025

Persistent Dichotomies in Psychology:

In studying the phenomena of recurring "threes" patterns in a variety of subjects, I encounter various other patterns, both numerical and geometric (not to mention sound patterns, taste patterns, etc...). However, my collecting and collating efforts have primarily been focused on a tabulation of different models of the "three". Yet in developing a model of explanation for the recurrence, I have encountered not only multiple examples of "two", but those who have made an effort to list examples of this recurring phenomena. For example, it has been referenced by Psychologists who have noticed that the pattern-of-two (called duality or dichotomy) is a persistence that the subject of Psychology has not moved away from since its inception,...and most importantly, has not even developed a term such as "trichotomization" to reference the persistent presence of the three pattern. And though one might well say there also is no formal reference to other repeating cognitive enumerations... e.g. quatornization for patterns-of-four, quintornization for patterns-of-five, sextonization for patterns-of-six, septonization for patterns-of-seven, octonization for patterns-of-eight, etc... such designated formalities would require a recognizable repetitiveness that patterns-of-two and patterns-of-three have attained as evidence by the presence volume in multiple subjects.

While we do find Cultural Anthropologists having recognized the recurrence of particular patterns having been adopted by one or another culture (enumerated, geometric, and otherwise...), we do not find those calling themselves "cognitive" psychologists particularly observant or interested in such behavior. Instead, they are primarily interested in what I view as soap opera or histrionic dramas of personal lives. Cognitive enumerations for most "cognitive" and other types of standard psychology professionals apparently become viewed as "extraneous" contemplatives on the order of some superstitious past-time or enculterated distraction having no real importance or relationship to human behavior worthy of their time for further investigation, despite the over-whelming evidence of recurring patterns of enumeration on fundamental structures of physiology, anatomy and long standing ideas in multiple sciences.

In the present context of looking at the persistence of dichotomies cropping up in several subjects, let me include the widely known idea of optical illusions, though we should consider the illusions of other sensory modalities (sound, touch, taste...) in such a review. The fact that so many optical illusion sport the reference of a dichotomy know doubt plays a role in another type of Psychology defined dichotomy called Cognitive Dissonance: "Cognitive dissonance is the mental discomfort experienced when a person holds two conflicting beliefs or when their actions don't align with their beliefs." Indeed, Psychology's bread and butter staple is to use a tool box containing many dichotomies and yet never once consider the idea of a developmental model of Trichotomization.

Opera AI response to persistent dichotomies

Opera AI generated response to the query "Psychological illnesses based on dichotomies".

Psychological Illnesses Associated with Dichotomous Thinking (Conditions most commonly associated with this cognitive distortion include):

Borderline personality disorder (BPD): This is the condition most frequently linked to dichotomous thinking, often referred to as "splitting". Individuals with BPD may abruptly shift from idealizing a person (seeing them as "all good") to devaluing them (seeing them as "all bad").

Depression: Dichotomous thinking can manifest as viewing situations as either a complete success or a total failure, which can contribute to low self-esteem and feelings of hopelessness.

Anxiety disorders: This type of thinking can lead to catastrophic thinking, where a person focuses solely on worst-case scenarios, magnifying potential negative outcomes and increasing anxiety.

Eating disorders: Perfectionism and the rigid self-evaluation common in eating disorders often involve all-or-nothing thought patterns.

Narcissistic personality disorder (NPD): Similar to BPD, individuals with NPD may engage in splitting as a defense mechanism to maintain their self-image.

Obsessive-compulsive disorder (OCD): Rigid thought patterns and a need for certainty can involve dichotomous thinking.

Schizophrenia was initially defined with the (Dichotomy-linked) word "Ambivalence" According to Eugen Bleuler.

Separately, the field of psychiatry has historically used and debated several broad classification "dichotomies", which are theoretical divisions of mental disorders, rather than symptoms experienced by patients.

Kraepelinian dichotomy: Proposed by Emil Kraepelin in the late 19th century, this classified severe mental illnesses into two primary groups: dementia praecox (now conceptualized as schizophrenia) and manic-depressive illness (bipolar disorder). While influential, modern research indicates significant overlap between these conditions, challenging the original strict division.

Nature vs. Nurture: The debate over whether mental illness is caused by genetics/biology (nature) or environment/upbringing (nurture) is now largely considered a false dichotomy. Most mental health professionals agree that disorders result from a complex interaction of biological, psychological, and environmental factors.

Whereas the extremes of dichotomous thinking is the general rule-of-thumb used to describe several "mental disorders", dichotomous thinking is not generally discussed in terms of extremism if a person's life does not display some extreme behavior which is disruptive to oneself and/or others. Multiplicity of usage where a given theme such as dichotomies, is an overlooked extreme. But you can't see it unless it is contrasted with a different dominant model of thought such as the use of trichotomies, though other patterns could well be used. Hence, a dominant use of dualistic thinking by a culture whose dominant institutions such as (government politics, government military (often defined in terms of theatrical labels such as actors, staging, audience...), government police forces... commerce, education, mental health, mathematics, computer language, optical illusions, sports, theatrical entertainment, etc... ) all use such a pattern, is an expressed extremism that is overlooked and viewed as normalcy.

Thus when a person such as a young student is experiencing a cognitive shift into trichotomization, their perceptions render a conflict with the so-called "real world" practices of demanding everyone abide by a rule-of-thumb involving dichotomies, whereby since they have no one training them in their perceptions involving trichotomies, conflicts arise in which they act out or turn inward whereby all the so-called intelligent professionals necessarily want to intervene by using some chemical, time-out, or dichotomous-structured type of restraint to force them into complying with some form of expected dichotomy dominant world-view orientation like so many other day to day binary thinking and acting automatons... including the hypocrisy of those practicing the dichotomous orientations of some this -or- that sexual orientation.

The idea of a person-specific developmental trend into a world-view framework of Trichotomization is so far removed from the radar scope of most people, it's no wonder there are troubling incidents in an enforced compliance to go along with a dichotomous world-view though one's own perspective is venturing into the realm of trichotomization which is just a label denoting the overlooked presence of a developmental shift in human consciousness and is not meant to characterize a particular dominance of the "three" of trichotomy over the "two" of dichotomy, whereby yet another king-of-the-hill type of thinking is used detrimentally. However, the use of a 1 (Reptilian brain), 2 (Old mammal brain), 3 (New mammal brain) designations do help to provide a closer modicum of understanding to the overall developmental trend of what we today term as consciousness.

Nonetheless, despite this philosophical excursion into the multiplicity of enumerations, the lack of a word such as "Trichotomization" in the purview of psychology other than in the form of viewing an interest in "threes" (or some other repetitive exercise) as a characteristic expression of an obsession, compulsion or both; is particularly problematic with respect to appreciate a developmental understanding about the development of human consciousness which is tied to a physiology whose underlying development exhibits the use of multiple three patterns... such as DNA's triplet code, three Germ layers and a three-pattern anatomy.

Understanding the etiology (cause) of a disease is often addressed by those who investigate the history of an individual, the species, society, etc... And yet, in researching the different types of history, what has been overlooked is the history of enumeration as a tool of human cognitive activity. Whereas one sees dualities and may describe as well as list a quantity of them— or sees trialities which are most frequently called triads, trinities, triunities, triples, etc., such studies of enumeration are most often deferred to Mathematicians or Anthropologists, who are to be noted as providing biased accountants which frequently exhibit how distracted such researchers actually are in their investigations as illustrated by their explanations involving digressions into making comparisons which are little more than elaborations of superficiality. In other words, their represented illustrations being used as examples are simplistic comparisons of surface-level cognitive activity whose origination remains as an elusive topic.

For example, an Anthropologist (or Mathematician) may present a record of different cultures who count in similar or dissimilar ways, and yet leave a reader in a state of oblivion as to how such a commonality might have arisen based on similar or dissimilar environmental circumstances affecting a similar or dissimilar physiology. All of them, including those researchers who follow them are resurrecting the same type of superficiality, though they think they are being more insightful simply because they have included a larger list of cultural examples. For example, one researcher lists religious triads from 3 cultures and another adds to that list with a list of 3 or 6 or 9 other cultures; yet the list remains as a list of religious triads. The enlarging list does not provide a list of other ideas involving triadic structures, even though one or another researcher may allude to the possibility for such an inclusion. And yet, when we come across someone who does list examples from different subjects, they too may not turn their investigations towards an understanding of human cognitive activity involving environmental influences on developmental biology. Far too often the researchers get distracted. They either begin to second guess themselves or reject ideas which seem too far astray from the conventions of their peers or those who are thought to be experts.

The idea that the human brain relies on the use of repeating patterns and some of those patterns exhibit a prominent 3-part reference, needs to be placed alongside those patterns of enumeration which are sometimes referenced... be it 1, 2, 4, 5, 6, 7, etc..., and placed into a graphic such as the hypothetical account displayed here:

Hypothetical graph showing distribution of cognitive patterns

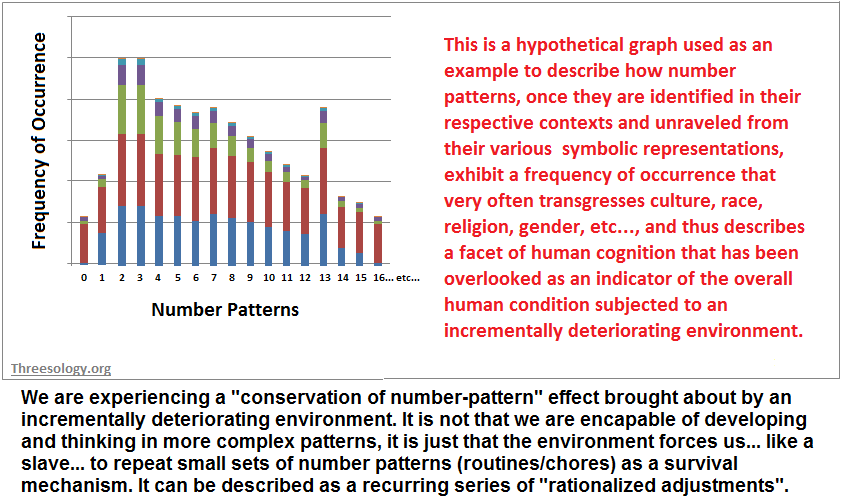
While number symbols themselves are sometimes used, number words or gestures also are part of the human cognitive repertoire. In other words, the brain of humans can use physiology in different ways to exhibit an expressiveness. For example, if I write the number "3" and another person writes the word "three" and another person taps their pencil three times, the same cognitive pattern is being exhibited. Instead of tapping a pencil or pen three times, they may fidget in a chair three times or three ways, or ask three questions, or speak about having three pets, or tell you they walked around a park three times, etc... Then again, they may hear a car horn being honked three times and then hear a dog bark three times or a crow caw three times, or see three planes in one day... etc., all of which may be registered as a recognizable theme to their active brain which does not adequately explain its functional activity or agenda which may differ than the socialized efforts of a given person in their era of existence.

Psychology, nor Philosophy, nor Mathematics, religion or any present day convention of presumed higher thinking has sought to present us with a graph exhibiting the distribution of patterns human cognition (thinking) is involved in. Yes, the graph is a hypothetical construction, but it nonetheless provides a visual representation of my own thinking about human thinking activity. As such, in my research, even due to my "threes" bias, I can see that the recurrent usage of patterns-of-two is high. Other enumerations do not show up as frequently, even though they may be long enduring with different levels of prominence in different eras... such as the "7" in the antiquities of religion tied to the observations of stars with a count of seven such as the Big Dipper, Pleiades, and the seven Planets ("wanterer") labeled as the Sun, Moon, Mercury, Venus, Mars, Jupiter, Saturn, which were visible without the aid of a telescope. (source: "planet." Encyclopædia Britannica, 2013.)

From this (List of Dualities) page of the wikipedia, we find more of the same dualistic referencing.

With respect to the persistence of "two" (dualities/dichotomies/pairs) in Psychology, we need to note the persistence of the pattern pre-dated psychology in the formula known as the ancient Chinese Ying/Yang, as well as in Mathematics and the current state of computer language which is dependent on the ON/OFF switching nature of an electrical circuit (making computers boxes of fast switches), though these latter three examples have exhibited attempts to move beyond the "two" and develop some measure of a "three" orientation, and there are individuals within the sphere of psychology who have exhibited three-patterned views... and yet none of them have an established orientation referencing a "threes" conceptual framework such as is encapsulated in the word "trichotomization":

Yin/Yang... the I-Ching (Book of Changes) exhibits the idea of eight "trigrams" though they are actually embellished dyads. A true trigram would display a one, two, three-line configuration and not repeat the one or two-lines in a three-pattern way. The Trigrams still conform to the old Yin/Yang philsophy where the single line symbolically represents the male penis and the double line symbolically represents the female vagina.

Mathematics... Pythagorean theorm (A² + B² + C², Trigonometry (Sine- Cosine- Tangent), Boolean Algebra (AND, OR, NOT gates used in computer language).
Binary Computer Language... Present efforts are under way to develop a Quantum Computer featuring a ternary/trinary language.
Psychology: (notice some use two names while other authors may include a middle initial as a third name reference)
- Sigmund Freud... Id- Ego- Superego, etc.
- Paul D. MacLean... Triune brain concept
- Robert J. Sternberg... Triarchic intelligence, Triangle love theory
- etc...
Philosophy: (A short list follows...)

Short list of philsophers using a pattern-of-three

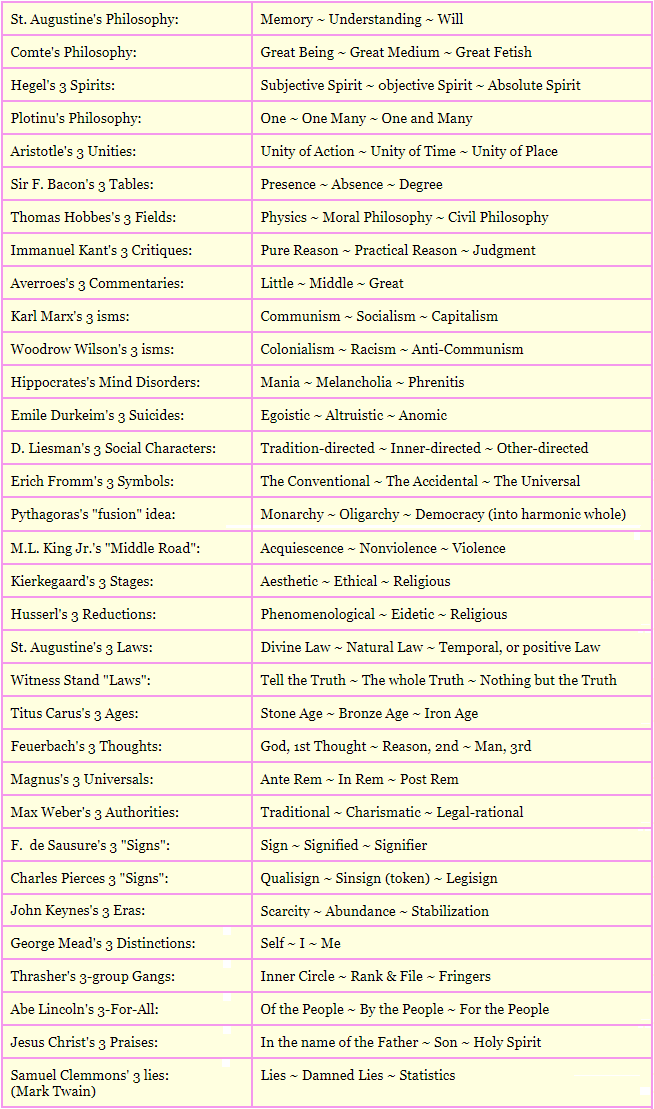
3-part Logic Thesis ~ Antithesis ~ Synthesis Indulgence ~ "Middle Way" ~ Ascetism Major Premise ~ Minor Premise ~ Conclusion Contradiction ~ Excluded Middle ~ Identity Principal
"God-ology": Omnipresent Omnipotent Omniscient	"Metaphysics-ology": What is real How change comes What is mind	Marxian "Dialectology": Unity of opposites Quantity & quality Negation of negation
Epistemology: How we know What is truth What is mind	Axiology: Nature of good Nature of beautiful Nature of religious	Ontology: Quality (1st-ness) Relation (2nd-ness) Representation (3rd-ness)

3 times the fool: You can fool some people some of the time - Some people all the time - But not all people all the time.
3 traditional syllogism forms: Categorical - Hypothetical - Disjunctive
3-patterned basic adult syllogism: All ravens are black - Jack is a raven - Therefore, Jack is black.
3-patterned basic child syllogism: Fuzzy Wuzzy was a bear - Fuzzy Wuzzy had no hair - Fuzzy Wuzzy wasn't fuzzy was he?

If we look at the Braille alphabet used for the blind, the reference that there are "six" dots can distract some researchers from even considering the presence of either 2 rows of 3 dots, or 3 rows of 2 dots. Cognitively speaking, the distinction may be an overall important one:

If we look at Morse Code, we again see a pattern-of-two with its characteristic dots and dashes, but in looking more closely, we find other enumerated patterns such as including the space between a dot and dash, and the standards by which Morse Code is to be used. In any respect, we see another example of a "conservation of Number". In addition, as an aside note. If we say that the dawn, noon, dusk positions of the Sun represent dots and the intervals in between as dashes, we have the sequence of dot dash dot dash dot... which means "End of Message". Whether it has any religious or other metaphysical meaning, I will leave that up to your own interpretation. Then again, you may prefer the image as that being 3 dots... meaning, SOS, or a call for assistance.

Date of Origination: Wednesday, March 26th, 2025... 5:17 AM
Initial Posting: Sunday, March 30th, 2025...12:52 AM
Updated Posting: Sunday, November 9th, 2025... 4:30 AM