
Page 21
http://threesology.org
Note: the contents of this page as well as those which precede and follow, must be read as a continuation and/or overlap in order that the continuity about a relationship to/with the typical dichotomous assignment of Artificial Intelligence (such as the usage of zeros and ones used in computer programming) as well as the dichotomous arrangement of the idea that one could possibly talk seriously about peace from a different perspective... will not be lost (such as war being frequently used to describe an absence of peace and vice-versa). However, if your mind is prone to being distracted by timed or untimed commercialization (such as that seen in various types of American-based television, radio, news media and magazine publishing... not to mention the average classroom which carries over into the everyday workplace), you may be unable to sustain prolonged exposures to divergent ideas about a singular topic without becoming confused, unless the information is provided in a very simplistic manner.
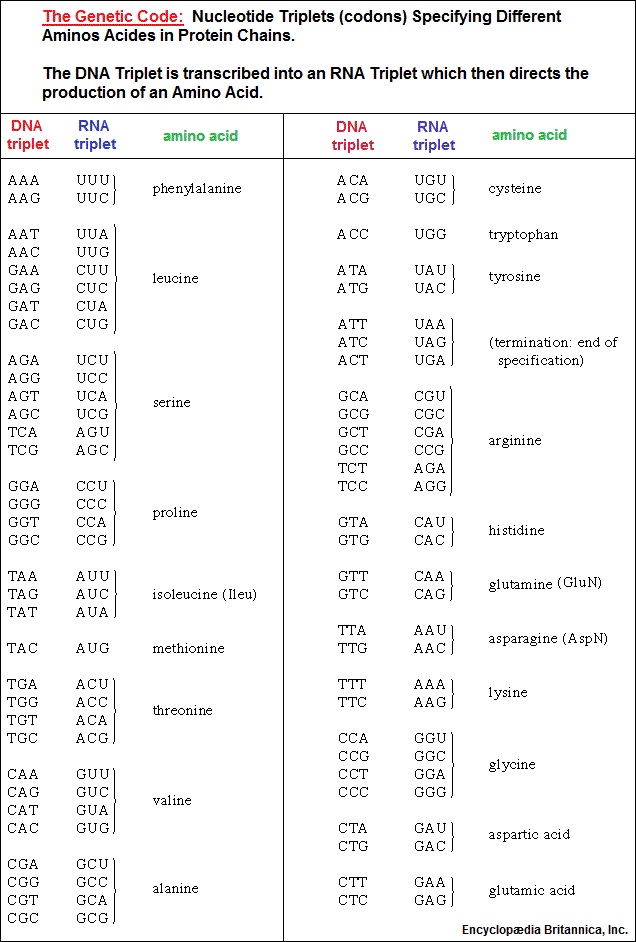
As previously noted, there are many instances of binary thinking presented in varying labels such as duality, dichotomy, biannual, opposite, dipole, chiral (right and left twisting), polar, twin, doublet, dimer, mirror image, cops and robbers, etc. And it is of some value to point out that some instances of describing a "three" might be more illustrative of the actual content if the usage of "three duplets" or "dual triplets" were used. For example, instead of saying DNA, RNA, (including AMP, ADP, ATP) have a constituent triplet codon system, it might be more descriptive to say they incorporate a structural triplet set of dualities. (For example: Adenine pairs with Thymine or Uracil; Cytosine pairs with Guanine). There are three "stable" nucleic acids (Adenine, Cytosine, Guanine), and two "floating" amino acids (Thymine for DNA and Uracil for RNA). I use the word "floating" because I imagine them to have been floating about in the primordial soup like two people awaiting to be introduced to groups most amenable to their disposed proclivities.
A always pairs with T through two hydrogen bonds, and G always pairs with C through three hydrogen bonds. Human DNA consists of 23 pairs of linear chromosomes containing three billion base pairs. Source: "Nucleic Acid." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Another example of a described "three" possessing patterns-of-two (binary) constituents, is found in the occasion of the three large sub-atomic particles labeled Electrons- Neutrons- Protons. Each of these are said to possess three-quarks and three anti-quarks, though no mention is ever made of three neutral-quarks... whether or not they exist. So, do we have three sets of two, or two sets of three? Which is more illustrative? Or how about if we say a set of three containing two sets of three? In any respect, the presence of a "two" is not mentioned, just like in some cases you may well find that no mention of a "three" is present when a "two" label is used.
And here is an example of a one- two- three circumstance that may not be taken out of the context of its subject area and combined with other similarly-patterned ideas:
Fatty Acids: If the carbon-to-carbon bonds are all single, the acid is saturated; if any of the bonds is double or triple, the acid is unsaturated and is more reactive. A few fatty acids have branched chains; others contain ring structures (e.g., prostaglandins). Fatty acids are not found in a free state in nature; commonly they exist in combination with the alcohol glycerol in the form of triglyceride (q.v.). Source: "Fatty Acid." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
While the second comment is not specifically about a one- two- three occurrence, it is provided in order that the following illustration might be seen as a three-to-one representation instead of its represented "four" labeling:
For those readers who think I am repeating myself, I will say that I am glad you're paying attention. Repetition can be a handy tool in an attempt to solidify an idea that may be lost when scrutinization of a single subject area is endorsed with one's full attention. In presenting a few two and three-patterned examples from different perspectives, we will be able to more readily ascertain whether or not it is feasible for the human mind to develop a trinary computation system. Just because we recognize the repetition of a three-pattern in different subjects does not mean it is particularly viable for implementation into a system on of thought with a dominant two- or binary pattern. In other words, we may not be able to use an electrical switching environment to developed a trinary computational system which can be more advantageous for larger cognitive issues, many of which we are not even cognizant of... like early Europeans unaware of the existence of the North American continent. A trinary system will be like the developmental usage of the triangle or the so-called Pythagorean Theorem illustrated above.
|
Pythagorean Theorem Proposition number 47 from Book I of Euclid's Elements, the well-known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)—or, in familiar algebraic notation, a2 + b2 = c2. Although the theorem has long been associated with the Greek mathematician-philosopher Pythagoras (c. 580–500 BCE), it is actually far older. Four Babylonian tablets, circa 1900–1600 BCE, indicate some knowledge of the theorem, or at least of special integers known as Pythagorean triples that satisfy it. Similarly, the Rhind papyrus, dating from about 1650 BCE but known to be a copy of a 200-year-old document, indicates that the Egyptians knew about the theorem. Nevertheless, the first proof of the theorem is credited to Pythagoras. The Pythagorean theorem has fascinated people for nearly 4,000 years; there are now an estimated 367 different proofs, including ones by the Greek mathematician Pappus of Alexandria (flourished c. 320 CE), the Arab mathematician-physician Tha-bit ibn Qurrah (c. 836–901), the Italian artist-inventor Leonardo da Vinci (1452–1519), and even U.S. President James Garfield (1831–1881). Source: "Pythagorean Theorem." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
We must ask why various constructs of "two" and "three" have fascinated humanity. While there are superstitions involving a variety of numbers, these do not crop up with the same frequency or intensity to which patterns-of-two and three do... though we might add a few number patterns nearby such as one, four, five, etc... Nonetheless, whereas we do not have a trinary computer system, patterns-of-three play a role. Patterns of seven, or one hundred twenty three, for example, do not. Again, there is an identifiable conservation of cognitive patterning taking place. This either means we humans, as a type of biological hardware configuration are not equipped to accept a software program detailing knowledge or perceptions beyond these conservations, or that in recognizing such a limitation, we are thus enabled to reach beyound the so-called "natural" intelligence and create a far more expansive "artificial" one.
While the identification of trinary systems are accessible to present day perceptions and both conventional and idiomatic (subject-jargonized) cognitive ordering skills, they are not necessarily adaptable to providing us with a computational system superior to the binary code; with respect to current models of described hardware in which to house such a trinary formula. In seeking an Artificial Intelligence, many are pursuing a course for creating a non-biological model because the human species, as represented by their business, government and religious practices; exhibit a model of intelligence with an underlying bad code that no computer programmer would deliberately create unless they were intoxicated on gut-wrenching narcotics.
And though some easily recognize the many ways in which a binary orientation exists in different conceptualizations, they are so eager to depart from this venture and explore the world of multiple trinary or singular forms. For example, when Leibniz rather naively claimed this reality to be the best of all possible worlds, not many readers saw the idea in the larger context of a 1, 2, 3 differentiation of cognitive excursions into an accumulated assessment of knowledge at that time. Far too many specialize and thus leave out the necessary amalgamation of different perspectives creating a larger view-scape of this reality, however small and simple- minded our ideas of today may nonetheless be seen in the centuries ahead.
The Best of All Possible Worlds In the philosophy of the 17th–18th-century philosopher Gottfried Wilhelm Leibniz, the present world of monads (infinitesimal psychophysical entities) coordinated in pre-established harmony. Among all possible worlds that God could have created, his actual choice of one over the others required a “sufficient reason,” which, for Leibniz, was the fact that this world was the “best”—despite the existence of evident evils, for any other “possible world” would have had evils of its own sort of even greater magnitude. Had it lacked a sufficient reason to explain its existence (and implicitly its contingency), the world for Leibniz would have existed of necessity. Voltaire's Candide (1759) was a satirical rejection of Leibniz's optimistic view of the world. Source: "Best of all possible worlds." Encyclopædia Britannica Ultimate Reference Suite, 2013.Few (if any) philosophers and theologians have been prepared to claim, with Leibniz, that the existing world is the best of all possible worlds. If it were not, Leibniz argued, what sufficient reason would God have had to create it? Apart from Leibniz's view, three positive strategies have been developed:
It is possible, of course, to combine these three positions, or elements of them, in attempting to offer an overall response to the problem of evil. Some thinkers have approached evil, or certain evils, from the opposite direction. They have argued not that evil presents an overwhelming problem for theism but that it provides an argument for a life after death in which the injustices and inequities of the present life are remedied. Source: "Religion, Philosophy of." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
The above, latter article continues comments involving mental constructs... that we humans construct reality and assign a given language to it. Such an idea is attributed to the philosophy of Ludwig Witgenstein, and are of need to be mentioned along with his interest in logic and mathematics... subjects we find being analytically applied to the question of computation as it is used to a search for the creation of an artificial intelligence.

Although he shared his family's veneration for music, Wittgenstein's deepest interest as a boy was in engineering. In 1908 he went to Manchester, England, to study the then-nascent subject of aeronautics. While engaged on a project to design a jet propeller, Wittgenstein became increasingly absorbed in purely mathematical problems. After reading The Principles of Mathematics (1903) by Bertrand Russell and The Foundations of Arithmetic (1884) by Gottlob Frege, he developed an obsessive interest in the philosophy of logic and mathematics. In 1911 Wittgenstein went to Trinity College, University of Cambridge, in order to make Russell's acquaintance. From the moment he met Russell, Wittgenstein's aeronautical studies were forgotten in favour of a ferociously intense preoccupation with questions of logic. He had, it seemed, found the subject best suited to his particular form of genius. Wittgenstein worked with such intensity on logic that within a year Russell declared that he had nothing left to teach him. Wittgenstein evidently thought so too and left Cambridge to work on his own in remote isolation in a wooden hut that he built by the side of a fjord in Norway. There he developed, in embryo, what became known as the picture theory of meaning, a central tenet of which is that a proposition can express a fact by virtue of sharing with it a common structure or “logical form.” This logical form, however, precisely because it is what makes “picturing” possible, cannot itself be pictured. It follows both that logic is inexpressible and that there are—pace Frege and Russell—no logical facts or logical truths. Logical form has to be shown rather than stated, and, though some languages and methods of symbolism might reveal their structure more perspicuously than others, there is no symbolism capable of representing its own structure. Wittgenstein's perfectionism prevented him from putting any of these ideas in a definitive written form, though he did dictate two series of notes, one to Russell and another to G.E. Moore, from which one can gather the broad lines of his thinking. Source: "Wittgenstein, Ludwig." Encyclopædia Britannica Ultimate Reference Suite, 2013. |

Perhaps Wittgenstein could have said that it takes something other than that which created a picture, to actually picture it. This idea is succintly described by a quote attributed to Einstein, dealing with efforts to solve problems created by a perspective incapable of seeing beyond its own finger-tips... thus requiring the vantage point of a different relativity.which created a picture, to actually picture it. This idea is succinctly described by a quote attributed to Einstein, dealing with efforts to solve problems created by a perspective incapable of seeing beyond its own finger-tips... thus requiring the vantage point of a different relativity.
Whether or not we think that the usage of a binary code is based upon the "persuasions" of multiple "natural" derivatives (doubling of cells, two eyes, ears, bipedal gait, hot/cold, life/death, etc...), it is nonetheless the result of a constructed reality. The usage of a trinary or non-symbol computational system that would exceed our present cognitive machinations and present us with a type and form of intelligence exceeding our own biological capability to develop a similar level of functioning; is thus made more real by being a defined possibility... as a graspable metaphysic. Like an explorer of the unknown... though we construct some plausible "what if" or "maybe" reality as a means to satisfy the development of a rationality; suppositions are of value even if the end result is a dead end of expectation. That which is found, IS FOUND, though its value may not be accurately assessed upon discovery or later initial examinations. The metaphysic has become a physic-al entity. As with other subjects, Metaphysics must be read from the perspective of a specialized generality:
The science of the world as a whole Another way in which metaphysicians have sought to define their discipline is by saying that it has to do with the world as a whole. The implications of this phrase are not immediately obvious. Clearly, a contrast is intended in the first place with the various departmental sciences, each of which selects a portion or aspect of reality for study and confines itself to that. No geologist or mathematician would claim that his study is absolutely comprehensive; each would concede that there are many aspects of the world that he leaves out, even though he covers everything that is relevant to his special point of view. By contrast, it might be supposed that the metaphysician is merely to coordinate the results of the special sciences. There is clearly a need for the coordination of scientific results because scientific research has become increasingly specialized and departmentalized; individual scientific workers need to be made aware of what is going on in other fields, sometimes because these fields impinge on their own, sometimes because results obtained there have wider implications of which they need to take account. One can scarcely see metaphysicians, however, or indeed philosophers generally, performing this function of intellectual contact man in a satisfactory fashion. It might then be supposed that their concern with the world as a whole is to be interpreted as a summing up and synthesizing of the results of the particular sciences. Plato spoke of the philosopher as taking a synoptic view, and there is often talk about the need to see things in the round and avoid the narrowness of the average specialist, who, it is said, knows more and more about less and less. If, however, it is a question of looking at scientific results from a wider point of view and so of producing what might be called a scientific picture of the world, the person best qualified for the job is not any philosopher but rather a scientist of large mind and wide interests. Metaphysics cannot be satisfactorily understood as an account of the world as a whole if that description suggests that the metaphysician is a sort of super-scientist, unlimited in his curiosity and gifted with a capacity for putting together other people's findings with a skill and imagination that none of them individually commands. Only a scientist could hope to become such a super-scientist. Metaphysics article Contributors:Bruce Withington Wilshire William Henry WalshA.C. Grayling Source: "Metaphysics." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
However, one can not use the word "Metaphysics" in speaking about the development of a trinary computational system. It is not part of the regular jargon of may lay or even specialized subjects. To use such a word invites negative, or "other-worldly" labeling that does not assist in getting the essential idea to be taken seriously. Use of the word "Metaphysic" is like speaking in a foreign language... in a type of specialized slang or jargon that may have different meanings of application like the inflections applied to the same word to express some subtle difference based on context and content of a given speaker. But, so too is the situation in which one attempts to convey an idea using information from multiple subject areas. Whereas a person may know one or two subjects quite well, and another or so slightly well; we find their knowledge of subjects to be measurable as one does the usage of a language in general. There are not that many people who have an understanding of multiple subject areas. Yet in trying to convey an idea developed from the information of multiple subjects to the limitations of ideas presented in the subject a given person may be comfortable with; presents us with problems in our efforts to communicate an idea if the view requires a vocabulary consisting of the words found in different subjects which create a whole new language... and with it, a new repertoire of ideas.
As an analogy, we can provide a short account of Pete Maravich, whose basketball prowess was ahead of its time, and beyond the ability of the public to fully appreciate what they were witnessing, since they had no former context in which to place the phenomena, that was a one-of-a-kind exhibition in depth and dimension (though watching him play was particularly different than reading about it years later). Some actually thought he wasn't particularly good since he could pass the ball to others on instinct, but their instinct was rooted in conventions far too amateurish for his playing ability, thus they missed the ball but he was blamed for the error. He was a player gifted in many ball playing respects, while others were talented only in one area of play. He was nicknamed "Pistol" Pete Maravich because of his lightning fast executions of play that others could not keep up with... just like a binary computational system will not be able to keep up with a trinary system.
American basketball player who was the most prolific scorer in the history of Division I men's college basketball and who helped transform the game in the 1960s and '70s with his ball handling and passing wizardry. A spectacular shooting star, Maravich rocketed through college and professional ranks driven by an insatiable desire to be the greatest that resulted in an eventful but short life. Some of Maravich's urge to excel was instilled in him by his father, Press Maravich, who was the head basketball coach at Clemson University and North Carolina State University before he took the reins at Louisiana State University (LSU). Maravich was compelled by his father to endlessly hone his basketball skills, and the practice methods of the teenaged Maravich are the stuff of legend, including dribbling while on marathon runs, while riding a bicycle, and out the window of a car while a passenger. In the process he perfected an array of moves that made the ball seem like an appendage to his body. On an individual basis, there appeared to be no scoring, passing, ball handling, faking, or mind-boggling maneuver Pistol Pete could not—or would not—attempt. In three varsity seasons at LSU under his father—in an era when freshmen were prohibited from playing with the varsity—he rang up a National Collegiate Athletic Association (NCAA) scoring record with 3,667 career points. He led all college scorers three straight times, averaging an NCAA record 44.5 points per game as a senior in 1969–70. On the court Maravich was the consummate showman; skinny, with a mop of tousled brown hair, and always wearing his trademark floppy socks, he electrified the LSU faithful at the John M. Parker Agricultural Coliseum. Off the court he was shy, almost reclusive except with close friends, and he drank, ultimately becoming an alcoholic. Maravich's professional career was marred by resentment over the $1.9 million contract (by far the highest-paying to date) he received when the Atlanta Hawks made him their first draft choice in 1970. By then Pistol Pete had grown into a finely tuned, 6-foot 5-inch (1.96-metre) guard, although his unlimited potential went largely unfulfilled in 10 NBA seasons. Injuries took their toll as he moved on to the New Orleans Jazz, with whom he won his only NBA scoring title with a 31.1 average in 1976–77. The franchise relocated to Utah in 1979, where Maravich's role diminished. Released by the Jazz, he finished his career with the Boston Celtics. After basketball he searched for a lifestyle that would bring him peace—running through vegetarianism, yoga, and Hinduism, among other pursuits before finding solace in Christianity. He died of a heart attack at age 40. Source: "Maravich, Pete." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Pete Maravich was a candle burning from both ends, like the behavior seen in those whose genius must come early or find its energy of illumination lost in darkness, such as the discovery of a new mathematics... A field in which large amounts of information can be consumed by way of a symbolized vocabulary enabling someone to construct a new language model like the concepts of the zero, algebra, geometry and the calculus. If Pete Maravich's genius had been in mathematics, literature, music or other art form, he would have transgressed the known conventions and created a new form, a new formula, or a new function. If Maravich's dad had been a mathematician or symphony conductor, the world might well have a different memory of him. Instead, he is a footnote to most of those who watched him, though there are some who can remember him as an unforgettable shooting star upon which one did not wish, but memorized as a flashing rainbow with its own unique intelligence... though the word "intelligence" is meant to convey an originality of expression that only a few were perceptive enough to grasp as an entity applicable to many different contexts.
The present binary formula of computation has been set up as a race course thought to be born anew by redesigning the landscape, including an infield parking lot, or by adding different types of races, horses and jockeys. However, embellishments do not change the underlying architecture of the track nor the premise of operation.
Subject page first Originated (saved into a folder): Thursday, November 13, 2014... 5:50 AM
Page re-Originated: Sunday, 24-Jan-2016... 08:51 AM
Initial Posting: Saturday, 13-Feb-2016... 10:59 AM
Updated Posting: Tuesday, 25-June-2019... 2:59 PM
Herb O. Buckland
herbobuckland@hotmail.com