
Page 35
http://threesology.org
Note: the contents of this page as well as those which precede and follow, must be read as a continuation and/or overlap in order that the continuity about a relationship to/with the typical dichotomous assignment of Artificial Intelligence (such as the usage of zeros and ones used in computer programming) as well as the dichotomous arrangement of the idea that one could possibly talk seriously about peace from a different perspective... will not be lost (such as war being frequently used to describe an absence of peace and vice-versa). However, if your mind is prone to being distracted by timed or untimed commercialization (such as that seen in various types of American-based television, radio, news media and magazine publishing... not to mention the average classroom which carries over into the everyday workplace), you may be unable to sustain prolonged exposures to divergent ideas about a singular topic without becoming confused, unless the information is provided in a very simplistic manner.
An analysis of different information in different contexts often relies on some sort of "trigram" analysis. For example, a detective may analyze fingerprints using there basic "Loop- Whorl- Arch" distinctions of variation. They may also seek out a blood type using the ABO blood-typing system (unless some other system is required). A third example is the examination of biological matter to ascertain the presence of one's (triplet coded) DNA... all the while they are trying to establish an "MO" (modus operandi... or mode of operation), and despite their unacknowledged usage of a binary system of analysis since criminals tend to see, and impulsively act on their given world from a pattern-of-two frame of reference. (Theirs is a world of various dichotomies such as black/white, rich/poor, red/green [traffic lights], kill or be killed, smart/dumb, strong/weak, etc.). A middle alternative is often side-stepped, discarded, or not a typical "plan of action" consideration.

whereas in many instances a pattern-of-three formula assists in solving a problem, as can a binary alternative, such patterns have their counter-part personalities in that they present us with problems specifically characterized with such numerically framed indices. For example:
|
The three-body problem The inclusion of solar perturbations of the motion of the Moon results in a "three-body problem" (Earth-Moon-Sun), which is the simplest complication of the completely solvable two-body problem discussed above. When Earth, the Moon, and the Sun are considered to be point masses, this particular three-body problem is called "the main problem of the lunar theory," which has been studied extensively with a variety of methods beginning with Newton. Although the three-body problem has no complete analytic solution in closed form, various series solutions by successive approximations achieve such accuracy that complete theories of the lunar motion must include the effects of the nonspherical mass distributions of both Earth and the Moon as well as the effects of the planets if the precision of the predicted positions is to approach that of the observations. Most of the schemes for the main problem are partially numerical and therefore apply only to the lunar motion. An exception is the completely analytic work of the French astronomer Charles-Eugéne Delaunay (1816–72), who exploited and developed the most elegant techniques of classical mechanics pioneered by his contemporary, the Irish astronomer and mathematician William R. Hamilton (1805–65). Delaunay could predict the position of the Moon to within its own diameter over a 20-year time span. Since his development was entirely analytic, the work was applicable to the motions of satellites about other planets where the series expansions converged much more rapidly than they did for the application to the lunar motion. Delaunay's work on the lunar theory demonstrates some of the influence that celestial mechanics has had on the development of the techniques of classical mechanics. This close link between the development of classical mechanics and its application to celestial mechanics was probably no better demonstrated than in the work of the French mathematician Henri Poincaré (1854–1912). Poincaré, along with other great mathematicians such as George D. Birkhoff (1884–1944), Aurel Wintner (1903–58), and Andrey N. Kolmogorov (1903–87), placed celestial mechanics on a more sound mathematical basis and was less concerned with quantitatively accurate prediction of celestial body motion. Poincaré demonstrated that the series solutions in use in celestial mechanics for so long generally did not converge but that they could give accurate descriptions of the motion for significant periods of time in truncated form. The elaborate theoretical developments in celestial and classical mechanics have received more attention recently with the realization that a large class of motions are of an irregular or chaotic nature and require fundamentally different approaches for their description. Source: "celestial mechanics." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Celestial mechanics is a fascinating subject. The above article is a very brief examination and is truncated in order to give reference to the existence of three-patterned ideas involving motion which will be referenced after the following insert to the three-body problem:
Physicists Discover a Whopping 13 New Solutions to Three-Body Problem Article from: Science Mag By Jon Cartwright Mar. 8, 2013, 4:30 PM 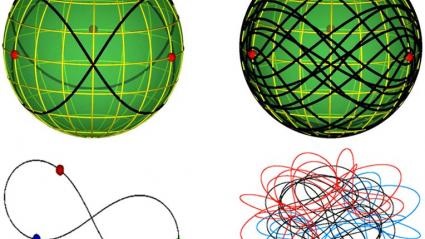
Shape up. Solutions to the three-body problem, such as the "figure eight" and "yarn," can be viewed on an abstract shape-sphere (top) or in real space (bottom). Milovan Šuvakov and Veljko Dmitrašinovic, Phys. Rev. Lett., (2013); Milovan Šuvakov and Veljko Dmitrašinovic /Institute of Physics Belgrade. It's the sort of abstract puzzle that keeps a scientist awake at night: Can you predict how three objects will orbit each other in a repeating pattern? In the 300 years since this "three-body problem" was first recognized, just three families of solutions have been found. Now, two physicists have discovered 13 new families. It's quite a feat in mathematical physics, and it could conceivably help astrophysicists understand new planetary systems. The trove of new solutions has researchers jazzed. "I love these things," says Robert Vanderbei a mathematician at Princeton University who was not involved in the work. He says he, in fact, spent all night thinking about the work. The three-body problem dates back to the 1680s. Isaac Newton had already shown that his new law of gravity could always predict the orbit of two bodies held together by gravity—such as a star and a planet—with complete accuracy. The orbit is basically always an ellipse. However, Newton couldn't come up with a similar solution for the case of three bodies orbiting one another. For 2 centuries, scientists tried different tacks until the German mathematician Heinrich Bruns pointed out that the search for a general solution for the three-body problem was futile, and that only specific solutions—one-offs that work under particular conditions—were possible. Generally, the motion of three bodies is now known to be nonrepeating. Specific repeating solutions have been hard to come by, however. The famed mathematicians Joseph-Louis Lagrange and Leonhard Euler had come up with some in the 18th century, but it wasn't until the 1970s, with a little help from modern computing, that U.S. mathematician Roger Broucke and French astronomer Michel Hénon discovered more. Until now, specific solutions could be sorted into just three families: the Lagrange-Euler family, the Broucke-Hénon family, and the figure-eight family, the last of which was discovered in 1993 by physicist Cristopher Moore at the Santa Fe Institute. The figure-eight family is so called because it describes three objects chasing one another in a figure eight shape. The Lagrange-Euler solutions are simpler, with the equally spaced bodies going around in a circle like horses on a merry-go-round. The Broucke-Hénon solutions are the most complex: Two objects dash back and forth on the inside, while the third object orbits around the outside. The discovery of 13 new families, made by physicists Milovan Šuvakov and Veljko Dmitrašinovic at the Institute of Physics Belgrade, brings the new total to 16. "The results are beautiful, and beautifully presented," says Richard Montgomery, a mathematician at the University of California, Santa Cruz, who was not involved with the discovery. Finding any solution is a daunting prospect. Three objects in space can be set off in infinite ways. Somehow, initial conditions—starting points, velocities, and so on—must be found that bring the objects back to those conditions so the whole dance can start over again. Šuvakov and Dmitrašinovic's method was to start with an existing solution on a computer simulation and then tweak its initial conditions until a new type of orbit materialized, as they report in a paper in press at Physical Review Letters. "What we did was the most simple-minded thing that you could do," Dmitrašinovic says. "We were shocked when we discovered all these things, and we were even more shocked when we discovered that they had not been discovered before us." Faced with so many new solutions, the Belgrade physicists invented a new classification system. They used an abstract space called a "shape-sphere," which describes the shape of the orbits in terms of the relative distances between the objects. Three spots around the sphere's equator mark where two of the particles would collide, and a line drawn over the ball, which must avoid those spots, maps how near the objects get to each other. The simplest solution on the shape-sphere is of the Lagrange-Euler family. It is just a single point, because it corresponds to all three objects maintaining the same distance apart by orbiting (in real space) in a circle. Others solutions are much more intricate, however. The researchers' new "yarn" solution looks like a ball of yarn on the shape-sphere, although its real space orbit looks even more complex—rather like a huge mass of spaghetti. (All the solutions can be viewed online.) Šuvakov and Dmitrašinovic separated all the orbits—including the previously known ones—into 16 families based on their shapes on the shape sphere. They then sorted these families into four classes based on symmetry and other properties of the shapes, the first which included all the previous solutions. The next step for the Belgrade physicists is to see how many of their new solutions are stable and will stay on track if perturbed a little. If some of the solutions are stable, then they might even be glimpsed in real life. Now, the only widely accepted three-body solution observed in space is a system made up of the sun, Jupiter, and one of the nearby Trojan asteroids, which make up a Lagrange-Euler type circle. But if we look at enough "exoplanet" systems beyond our own, we might see some of the new, more complex solutions, too, such as a solar system that looks like a heap of spaghetti. "Observational astronomy is moving very quickly forward," Dmitrašinovic says. But he adds that spotting one of the solutions will still be very difficult. "It will take a while. I'm pretty sure it won't happen tomorrow." |
Kepler's laws of planetary motion In astronomy and classical physics, (these are) laws describing the motions of the planets in the solar system. They were derived by the German astronomer Johannes Kepler, whose analysis of the observations of the 16th-century Danish astronomer Tycho Brahe enabled him to announce his first two laws in the year 1609 and a third law nearly a decade later, in 1618. Kepler himself never numbered these laws or specially distinguished them from his other discoveries. Kepler's three laws of planetary motion can be stated as follows:
Knowledge of these laws, especially the second (the law of areas), proved crucial to Sir Isaac Newton in 1684–85, when he formulated his famous law of gravitation between Earth and the Moon and between the Sun and the planets, postulated by him to have validity for all objects anywhere in the universe. Newton showed that the motion of bodies subject to central gravitational force need not always follow the elliptical orbits specified by the first law of Kepler but can take paths defined by other, open conic curves; the motion can be in parabolic or hyperbolic orbits, depending on the total energy of the body. Thus, an object of sufficient energy—e.g., a comet—can enter the solar system and leave again without returning. From Kepler's second law, it may be observed further that the angular momentum of any planet about an axis through the Sun and perpendicular to the orbital plane is also unchanging. The usefulness of Kepler's laws extends to the motions of natural and artificial satellites as well as to unpowered spacecraft in orbit in stellar systems or near planets. As formulated by Kepler, the laws do not, of course, take into account the gravitational interactions (as perturbing effects) of the various planets on each other. The general problem of accurately predicting the motions of more than two bodies under their mutual attractions is quite complicated; analytical solutions of the three-body problem are unobtainable except for some special cases. It may be noted that Kepler's laws apply not only to gravitational but also to all other inverse-square-law forces and, if due allowance is made for relativistic and quantum effects, to the electromagnetic forces within the atom. Source: "Kepler's laws of planetary motion." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Newton's Laws of Motion (Newton's laws explain) relations between the forces acting on a body and the motion of the body, first formulated by Isaac Newton. Newton's first law states that, if a body is at rest or moving at a constant speed in a straight line, it will remain at rest or keep moving in a straight line at constant speed unless it is acted upon by a force. This postulate is known as the law of inertia. The law of inertia was first formulated by Galileo Galilei for horizontal motion on Earth and was later generalized by René Descartes. Before Galileo it had been thought that all horizontal motion required a direct cause, but Galileo deduced from his experiments that a body in motion would remain in motion unless a force (such as friction) caused it to come to rest. Newton's second law is a quantitative description of the changes that a force can produce on the motion of a body. It states that the time rate of change of the momentum of a body is equal in both magnitude and direction to the force imposed on it. The momentum of a body is equal to the product of its mass and its velocity. Momentum, like velocity, is a vector quantity, having both magnitude and direction. A force applied to a body can change the magnitude of the momentum, or its direction, or both. Newton's second law is one of the most important in all of physics. For a body whose mass m is constant, it can be written in the form F = ma, where F (force) and a (acceleration) are both vector quantities. If a body has a net force acting on it, it is accelerated in accordance with the equation. Conversely, if a body is not accelerated, there is no net force acting on it. Newton's third law states that when two bodies interact, they apply forces to one another that are equal in magnitude and opposite in direction. The third law is also known as the law of action and reaction. This law is important in analyzing problems of static equilibrium, where all forces are balanced, but it also applies to bodies in uniform or accelerated motion. The forces it describes are real ones, not mere bookkeeping devices. For example, a book resting on a table applies a downward force equal to its weight on the table. According to the third law, the table applies an equal and opposite force to the book. This force occurs because the weight of the book causes the table to deform slightly so that it pushes back on the book like a coiled spring. Newton's laws first appeared in his masterpiece, Philosophiae Naturalis Principia Mathematica (1687), commonly known as the Principia. In 1543 Nicolaus Copernicus suggested that the Sun, rather than the Earth, might be at the centre of the universe. In the intervening years Galileo, Johannes Kepler, and Descartes laid the foundations of a new science that would both replace the Aristotelian worldview, inherited from the ancient Greeks, and explain the workings of a heliocentric universe. In the Principia Newton created that new science. He developed his three laws in order to explain why the orbits of the planets are ellipses rather than circles, at which he succeeded, but it turned out that he explained much more. The series of events from Copernicus to Newton is known collectively as the scientific revolution. In the 20th century Newton's laws were replaced by quantum mechanics and relativity as the most fundamental laws of physics. Nevertheless, Newton's laws continue to give an accurate account of nature, except for very small bodies such as electrons or for bodies moving close to the speed of light. Quantum mechanics and relativity reduce to Newton's laws for larger bodies or for bodies moving more slowly. Source: "Newton's laws of motion." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
As noted, Newton's description of laws for large bodies does not fair too well for smaller bodies such as explaining the behavior of atomic particles. Nonetheless, they presented scientists with a crude map to unraveling the treasures now being found and sought after in physics. Similarly, the many divergent bits of information being supplied by an analysis of AI and 3sology is a set of crude implements being offered as a means to begin a more extensive foraging into the rather virgin jungle of AI considerations. What implement would you use to forage out a path if no ready-made implements are at hand or even known? What good is it to speak of a machete or destination, if such ideas are not equivalently forthcoming in our vocabulary, much less as an image to contemplate? Such was the case when so many other inventions were discovered. If all lies and their developmental industries are described as truth, then the truth we seek must be discovered in ways which present truths are not capable of considering. Classical approaches and answers to new problems may help us feel some affinity with notable figures of the past, but reverenced sentimentality can be over-valued and cause us to overlook a basic cognitive pattern as a "modus operandi" of our brain processing subjected to given environmental circumstances.
Three classical problems: Although Euclid solves more than 100 construction problems in the Elements, many more were posed whose solutions required more than just compass and straight edge. Three such problems stimulated so much interest among later geometers that they have come to be known as the "classical problems":
Even in the pre-Euclidean period the effort to construct a square equal in area to a given circle had begun. Some related results came from Hippocrates. others were reported from Antiphon and Bryson; and Euclid's theorem on the circle in Elements, Book XII, proposition 2, which states that circles are in the ratio of the squares of their diameters, was important for this search. But the first actual constructions (not, it must be noted, by means of the Euclidean tools, for this is impossible) came only in the 3rd century BC. The early history of angle trisection is obscure. Presumably, it was attempted in the pre-Euclidean period, although solutions are known only from the 3rd century or later. Source: "Mathematics." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
Early peoples thought that the stars were fixed in the sky and therefore existed as static bodies of reference. But further examination over time made by multiple observers showed that the bodies were dynamic. A celestial body which appeared to be static may well be moving at incredible speed, but the huge distances from our Earthly point of reference does not enable us to easily determine motion. The same binary formula has been applied to ideas concerning the Universe. Some have said it is static, while others have claimed it to be in motion. Some say it is a closed system, others say it is open. Some say it has a positive curvature, while others say it has a negative curvature. And there are those who may accept some admixture thereof, to present a third option. However, let us also make note that a trinary model of the Universe's shape has been offered. Some have claimed that it is flat, some have said it is spherical, and still others have offered the opinion that it is saddle-shaped. Take a look at some representative images concerning these three ideas:
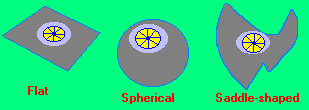 (What sort of animal is this saddle for?) |
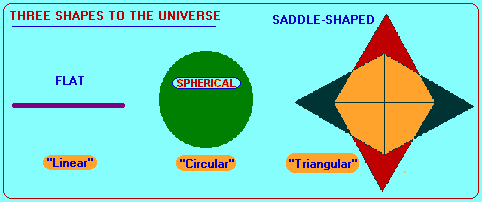 | |
 |
 |
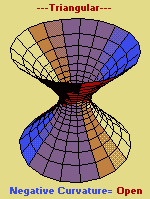 |
And those who say humanity uses a "one" pattern when speaking of a single God over-seeing the Universe no matter what shape it may have, this idea must be subjected to a greater scrutiny in order to reveal that humanity does not have a singular God, it has multiple gods with a singular name. Religions generally think that their belief concerns a one, true god... and everyone else has some entity attempting to masquerade as theirs. There is no Universal religion which is universally accepted as the "One" which encompasses all beliefs. Different religions think their interpretations have cornered the market on the concept of God, and therefore place it in a position of supremacy. Hence, we do not have one God, but multiple gods presented as being singularly important, but allowing for the same level of singular supremacy to multiple variations. If all beliefs are offered as facsimiles, then they are not an actuality.
While such a philosophical excursion can provoke disdain from some readers, it is meant to bring to mind the situation in which it is well known that the human mind can indulge in fantasy and madness... both of which are variations of rationality, though time and place may have some define individual situations as an irrationality. Take for example the situation described by Julian Jaynes in his examination of the Iliad and the Odyssey poems whose content is described as providing evidence for what can be described as a prevailing schizophrenia during the period of history in which the two poems are centered. His book "The Origin of Consciousness in the breakdown of the bicameral mind".
From pages 201-202 of Jaynes' (soft cover) book [ISBN 0-395-56352-6]:
"I have endeavored (in these two chapters) to examine the record of a huge time span to reveal the plausibility that man and his early civilizations had a profoundly different mentality from our own, that in fact men and women were not conscious as are we, were not responsible for their actions, and therefore cannot be given the credit or blame for anything that was done over these vast millennia of time; that instead each person had a part of his nervous system which was divine, by which he was ordered about like any slave, a voice or voices which indeed were what we call volition and empowered what they commanded and were related to the hallucinated voices of others in a carefully established hierarchy."
Julian Jaynes provides examples of this early mentality by providing distinctions between the content of the Iliad and the later Odyssey. Whereas the Iliad provides references to the god-controlled (Greek) human, the Odyssey provides us with a clear view of how the mind of (Greek) peoples began to change and take a much more personalized account of their actions, with the gods playing an increased subsidiary role. An interesting example of the changing bicameral state of mind can be seen in a short passage from Book I of the Odyssey:
In the present age, we sometimes encounter those who think that an occurrence is due to a direction given by God, an angel, Jesus, etc., or that they have received a heaven-sent "sign" especially for them. That in one way or another they are a "chosen" one for a particular task, whether that task is widely recognized and acknowledged or not. We of the present will frequently encounter the expression "Oh My God" (instead of "Oh Our God") and there is the utilization of the idea involving "god parents" for certain individuals attending the baptism of a child. The idea of "god parents" gives me the impression of a time when adult humans had the mentality of children and the voice of one or more gods acted as a directing parent.
With respect to differences in the occurrence of the Bicameral mentality, Julian Jaynes has this say on page 194:
...For just as we know that cultures and civilizations can be strikingly different, so we must not assume that the bicameral mind resulted in precisely the same thing everywhere it occurred. Difference in populations, ecologies, priests, hierarchies, idols, industries, all would, I think, result in profound differences in the authority, frequency, ubiquity, and affect of hallucinatory control.
On page 221, Jaynes presents the idea of a developmental certainty and completeness by offering the following as suggestions as to what influenced a (non- re-experiencing) change from a Bicameral frame of mind to what he calls consciousness:
- The weakening of the auditory by the advent of writing.
- The inherent fragility of hallucinatory control.
- The unworkableness of gods in the chaos of historical upheaval.
- The positing of internal cause in the observation of difference in others.
- The acquisition of narratization from epics.
- The survival value of deceit.
- A modicum of natural selection.
a related example of how humans might think they are in touch with (a) god (page 264, "The Uses of the Past, Profiles of Former Societies" ©1952, Herbert J. Muller):
every man, nay, every boy and wench that could read English,
thought they spoke with God Almighty."
Note: some forms of so-called mental illness are defensive measures to protect a person from an otherwise hostile social environment that can not readily appreciate their world-view. It is a perspective that Ronnie D. Laing might want to refer to, in some instances, as Super-sanity. (With the idea of "Super-sanity", we now have a trio: Insanity- Sanity- Super-sanity).
In making a connection between vocal utterances and a reference to some form of deity, the gospel of John (1:1) provides us with a unique description:
(Certain types of language, of writing (symbols), of speech, was interpreted as a God, and the person possessing one or more of said items, was seen as someone that was in direct communication with God. Such illiteracy, naivete and gullibility exists to this day.)
In short and simplistically, Jaynes' book refers to the characters in Homer's Iliad and Odyssey (circa 850 BC) as hearing the voices of one or more gods due to a difference in brain activity, if not underlying structural formation as well, perhaps in the sense that inter-connectivity amongst brain processes were in a developmental state (and some believe is the present case as well). It suggests the existence of a schizophrenic-like perspective which prevailed at the time as a cultural norm amongst the people and was therefore not recognized as bizarre, strange, weird or some type of mental illness (that some have suggested is presently represented in various business, government and religious models). Whether or not every single person exhibited such a mental state is up for debate, but it did exist amongst some important people according to Homer's account. However, let us be circumspect and not focus primarily on the ancient Greeks as having any particular monopoly for exhibiting this particular mental state. Let us suspect it was a world-wide phenomena that was (and in most respects is) taken for granted as normal behaviour.
According to a Wikipedia citation about --- Bicameralism ---, the psychiatrist Iain McGilchrist, in his book The Master and His Emissary (ISBN 0300168925, paperback), says that Jayne's hypothesis was "the precise inverse of what happened" and that rather than a shift from bicameralism there evolved a separation of the hemispheres. This may then suggest a rudimentary form of Corpus Callosum and a brain that began with a "Monocameralism." While casts of skulls do not today readily provide any indication of this, an understanding of how present research in the Corpus Callosum's role as an intermediary between present day brain hemispheres may be of value in helping us to unravel some glimpse as to how a developing brain may have produced a whole different world view to people in past ages. In order to do so, it is necessary to appreciate that early human brains, even just a few thousand years ago may have been internally structured different than what we of today consider "normal."
what if, during the age of the Iliad and Odessy, the human brain literally functioned differently, or the same as today but with slightly primitive features which created manifest conditions of "hearing voices" that received a culture-wide approval of being the voices of one or more gods and wer not interpreted as brain dysfunction as some are defining today? Is the present binary "orientation" of computer language a representation of an earlier mind-set put back into wide-spread social motion?
Excitation or Inhibition?
Juliana S. Bloom and George W. Hynd
The corpus callosum is the major neural pathway that connects homologous cortical areas of the two cerebral hemispheres. The nature of how that inter-hemispheric connection is manifested is the topic of this review; specifically, does the corpus callosum serve to communicate an inhibitory or excitatory influence on the contralateral hemisphere? Several studies take the position that the corpus callosum provides the pathway through which a hemisphere or cortical area can inhibit the other hemisphere or homologous cortical area in order to facilitate optimal functional capacity. Other studies suggest that the corpus callosum integrates information across cerebral hemispheres and thus serves an excitatory function in inter-hemispheric communication. This review examines these two contrasting theories of inter-hemispheric communication. Studies of callosotomies, callosal agenesis, language disorders, theories of lateralization and hemispheric asymmetry, and comparative research are critically considered. The available research, no matter how limited, primarily supports the notion that the corpus callosum serves a predominantly excitatory function. There is evidence, however, to support both theories and the possibility remains that the corpus callosum can serve both an inhibitory and excitatory influence on the contralateral hemisphere.
Subject page first Originated (saved into a folder): Thursday, November 13, 2014... 5:50 AM
Page re-Originated:Sunday, 24-Jan-2016... 08:51 AM
Initial Posting: Saturday, 13-Feb-2016... 10:59 AM
Updated Posting: Saturday, 31-March-2018... 3:10 PM
Herb O. Buckland
herbobuckland@hotmail.com