(Key Signature) in musical notation, the arrangement of sharp or flat signs on particular lines and spaces of a musical staff to indicate that the corresponding notes, in every octave, are to be consistently raised (by sharps) or lowered (by flats) from their natural pitches. (The keys of C major and A minor, having no sharps or flats, have no key signature.) The key signature is placed after the clef indication (treble or bass, for example) at the beginning of a staff or after a double bar line—the separation necessary for a change of signature—within a staff. In Western tonality, specific groupings represent the major and minor keys.

One flat appears as a key signature in some of the earliest sources that use staff notation, dating from the 11th or 12th century, a practice that survives in printed books of plainchant (see Gregorian chant). The concept was universally adopted with staff notation, but not until the late 18th century was the modern system of keys and associated fixed key signatures fully developed. Beginning in the late 19th century and continuing into the 21st, composers who challenged traditional tonality often used the notation in new ways. Some have marked notes with accidentals throughout, even when using a key signature, and others have mixed sharps and flats in the same signature.

In orchestral scores since the late 18th century (in the music of Joseph Haydn and later composers), different key signatures may appear simultaneously; some of the different instruments require transposition (e.g., fingering a C to sound a B-flat) because of differences in fingering systems (clarinets, for example) or changes in tube length (in horns and trumpets). In some orchestral scores published since the 1920s, however, this practice is not followed, and all instruments are indicated to sound as written. (See also instrumentation; transposing musical instrument.)

(A Transposing Musical Instrument is an) instrument that produces a higher or lower pitch than indicated in music written for it. Examples include clarinets, the English horn, and saxophones. Musical notation written for transposing instruments shows the relative pitches, rather than the exact pitches, produced. Writing in this manner is a historical convention that often allows players to switch from a given instrument to a related one without relearning fingerings and other techniques (as from E♭ (E flat) clarinet to B♭ (B flat) clarinet or from English horn to oboe). The instrument name, as in the case of the B♭ (B flat) clarinet, often indicates the pitch resulting when the player sounds the note written as C. If the actual pitch is lower (or higher) than the notated pitch, the written music must be adjusted upward (or downward) by the same amount. Thus, in the key of C major the music for the B♭ (B flat) clarinet must be written in the key of D major.

Although most transposing instruments belong to the woodwind and brass families, transposing keyboard instruments have also been built. The piccolo, contrabassoon, and other instruments whose parts are written an octave above or below the actual pitch (as c' above c) are not considered transposing instruments.

(Mode) in music, any of several ways of ordering the notes of a scale according to the intervals they form with the tonic, thus providing a theoretical framework for the melody. A mode is the vocabulary of a melody; it specifies which notes can be used and indicates which have special importance. Of these, there are two principal notes: the final, on which the melody ends, and the dominant, which is the secondary centre.

Ancient Greek modes

The modes of Greek antiquity were placed by theorists in orderly fashion within a larger context. Although the modes were a series of seven-note diatonic scales (i.e., containing five whole tones and two semitones), the nucleus of the tone system was the tetrachord—a group of four consecutive notes (as, from C to F on the piano) comprising the interval of a fourth. Except in late antiquity, the notes were always arranged in a descending order, the basic tetrachord consisting of two whole tones and one semitone: E–D–C–B. Two such tetrachords, separated from one another by a whole tone, formed the so-called Greek Dorian mode: E–D–C–B A–G–F–E. The Dorian mode was taken as a basis for the construction of the larger system. Its single-octave range was extended by the addition of a third tetrachord, A–G–F–E, on top and of a fourth tetrachord, E–D–C–B, at the bottom. In contrast to the two inner tetrachords, which were separated by a whole tone, each outer tetrachord was linked with the neighbouring inner one by a shared note:

Because the combination of the four tetrachords yielded a range of two octaves minus one whole tone, a low A was added by theorists to achieve the following diatonic two-octave system: A G F E D C B A G F E D C B A. This two-octave row, or disdiapason, was called the Greater Perfect System. It was analyzed as consisting of seven overlapping scales, or octave species, called harmoniai, characterized by the different positions of their semitones. They were termed as follows (semitones shown by unspaced letters):

Although the names of the harmoniai were identical with those of the Greek modes, the harmoniai were instead projections of the modal patterns into the more extensive Greater Perfect System. The modes proper were termed tonoi, their essence being their interval pattern. On the kithara or lyra (the two basic plucked stringed instruments of ancient Greece) the tonoi were produced either by the basic tuning or by the raising or lowering of one or more of the strings by a semitone. Thus, the seven tonoi would sound within the octave E–E as follows (black notes indicate changes from the Dorian tuning):

Greek theory distinguished three different genera of tetrachords, producing an additional variety of modes. The previously described tetrachord (two descending whole tones plus one semitone) was called diatonic. There were also chromatic and enharmonic genera. The two tones bounding the tetrachord were fixed and always formed a perfect fourth; the two inner tones were movable. The chromatic tetrachord consisted of a minor third (encompassing 1½ whole tones) plus two semitones, the enharmonic tetrachord of a major third (encompassing two whole tones) plus two approximate quarter tones: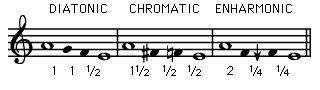

Also prominent in Greek music was the concept of ethos, which ascribed certain ethical characteristics to the different modes. The Dorian mode was preferred because of its strong and virile character; the Phrygian mode was ecstatic and emotional, the Lydian mode intimate and lascivious. In the Republic Plato stressed the educational values of the Dorian mode and warned against the softening influence of the Lydian ode.

In early Greek antiquity a system of modal categories developed, referred to as nomoi (singular, nomos, “law”). The nomoi represented modes in that they were characterized by distinctive melodic formulas suited to different song types. The performers were free to improvise within the boundaries of these modal formulas.

Byzantine chant molded the features of early Christianity with Hellenic and Oriental traits, including the Syrian okto-e-chos, and achieved a brilliant and distinctive style that served as a prototype for the chant of the Greek Orthodox Church. The eight e-choi of the Byzantine okto-e-chos were divided into four authentic and four plagal (derived) forms. The most common classification of the Byzantine modes was in terms of typical initial and final notes of melodies in a given mode, with the characteristic distinctions as follows (the orderly progression of notes in each series should be observed).

The above classification reflects only two of various characteristics (not all completely clarified by modern scholars) that gave the modes their identity.

Plainchant, or plainsong, is also known as Gregorian chant and forms the core of the musical repertoire of the Roman Catholic Church. It consists of about 3,000 melodies collected and organized during the reigns of several 6th- and 7th-century popes. Most instrumental in codifying these chants was Pope Gregory I.

The eight modes

Melodically, Gregorian chants are based on eight different modes, often called church modes. Seven of them were given names identical with those used in the musical theory of ancient Greece: Dorian, Hypodorian, Phrygian, Hypophrygian, Lydian, Hypolydian, and Mixolydian, while the name of the eighth mode, Hypomixolydian, was adapted from the Greek. Each mode comprises a diatonic scale with the compass of one octave. The modes are classified by their finalis, the usual final note of a melody in that mode. Each of the four notes of the tetrachord D–E–F–G serves as the finalis of an “authentic” mode (see chart below).

An authentic mode consists of a pentachord (a succession of five diatonic notes) followed by a conjunct tetrachord, for example:

But the tetrachord may be added below rather than above the pentachord, thus generating a “plagal” mode:

In either case the finalis falls on the lowest note of its pentachord. Each authentic mode has a correlated plagal mode, which is identified by the prefix Hypo. In the following chart of the eight church modes, the finalis is marked by a capital letter:

The tones of the Hypomixolydian mode are identical with those of the Dorian, but the two modes differ in the location of their finalis. The character of the church modes was further determined by a number of distinctive melodic formulas, and sometimes a particular ethos was attributed to the different modes.

Contrary to the Byzantine classification, which lists first the four authentic and then the four plagal modes, the Roman classification alternates the authentic and plagal modes, so modes with the same finalis follow each other. This principle underlies the medieval fourfold system of the so-called maneriae (Latin: “manners”), a division of the modes into four pairs. The first pair, or protus maneria, includes the Dorian and Hypodorian modes; the second, or deuterus, the Phrygian and Hypophrygian; the third, or tritus, the Lydian and Hypolydian; and the fourth, or tetrardus, the Mixolydian and Hypomixolydian.

Gradual emergence of major and minor tonality

The strict consistency of the system of church modes was gradually weakened by the appearance of B♭ (B flat) in addition to B ♯ (B sharp), although the two notes never occurred in succession. The main reason for the use of a tone not included in the basic scale pattern was that medieval musicians sought to avoid the tritone F–B. The tritone (so called because it includes three whole tones) was considered an undesirable interval sharply contrasting with the perfect fourth F– B♭ (F-B flat). The substitution of B♭ (B flat) for B ♯ (B sharp) changed the character of a mode. For example, the Lydian mode with a flattened B was identical with the modern major mode, specifically, with the F–major scale (F G A B♭ C D E F); and the Dorian mode with a flattened B generated a minor mode corresponding to the natural D minor scale (D E F G A B♭ C D).

Nevertheless, for centuries medieval theorists considered these alterations as special forms of the Lydian or Dorian mode rather than as new modes. The reluctance to acknowledge the existence of additional modes is reflected in the so-called musica ficta. According to this practice, musical notation appears to conform strictly to the system of church modes but presupposes that the performer makes certain adjustments by raising or lowering a note through the insertion of a sharp or flat.

Two different developments occurring between the 12th and the 16th centuries resulted in a radical change in modal theory: an infiltration of folk music into the ecclesiastical and secular art forms and the steadily evolving fabric of harmony destined to unify the growing complexity of polyphonic (many-voiced) musical texture. Finally, a theorist, Heinrich Loris, commonly known by his assumed name Henricus Glareanus, sanctioned the coexistence between the old church modes and the emerging major and minor modes. In his Dodecachordon (1547; from Greek do-deka, “twelve,” and chorde-, “string”), perhaps the most significant musical treatise of the time, Glareanus enlarged the system of the eight church modes by adding the following four:

The Ionian and Hypoionian modes correspond to the major mode, the Aeolian and Hypoaeolian modes to the “natural” minor mode. The 12 modes of the Dodecachordon comprise authentic and plagal structures with tonal centres on the notes C, D, E, F, G, and A, without recourse to sharpened or flatted tones. Glareanus mentions another two modes: the Locrian and the Hypolocrian, having B as their tonal centre. But because in these two modes B and the fifth degree above it, F, form a “false” (i.e., diminished, or flattened) fifth (another form of the forbidden tritone), Glareanus states that for practical purposes only 12 modes are available.

The growing complexity of polyphonic music caused the distinction between authentic and plagal modes to become more and more irrelevant, and, as a result, the number of modes was virtually reduced to only six. The further development of art music in the Western Hemisphere is characterized by the gradual abandonment of the old ecclesiastical modes in favour of the dual major-minor system that dominated 18th- and 19th-century harmony. This system is often termed tonal, in contradistinction to that of the church modes; in fact, some 20th-century works reviving the patterns of the old church modes, as well as folksongs that occasionally use them, are often termed modal. Nevertheless, major and minor scale patterns have all essential characteristics of modes and should therefore be evaluated as such...

Divided sharps

The second type (following the "Short Octave") of exceptional keyboard arrangement was originally required by the so-called meantone tuning system generally used in the 16th–18th centuries. Meantone tuning provided significantly purer tuning for a relatively small number of tonalities than does equal temperament, the system now in use (in which all tonalities are somewhat out of tune; see tuning and temperament), but only at the expense of restricting the usefulness of the remaining tonalities. This characteristic arose because in meantone tuning each of the raised keys could be used in only one way: for example, if the key between D and E was tuned to E♭ (E flat), it could not be used as D♯ (D sharp) without retuning. One solution was to build keyboards with the raised keys divided, the front half of the key sounding the appropriate sharp while the back half sounded the equivalent flat. The keys most commonly divided were A♭/G♯, E♭/D♯, and B♭/A♯. Instruments with up to three divided keys in each octave were commonly made in the 16th and 17th centuries, especially in Italy. Since the 1590s still more complicated keyboards have been built, permitting even more refined tunings; some in the 19th century had more than 50 keys per octave. Instruments have also been made with the octave divided into 24 rather than 12 equal parts to permit playing music utilizing quarter-tone intervals.

Metaphysics and number theory

According to Aristotle, number speculation is the most characteristic feature of Pythagoreanism. Things “are” number, or “resemble” number. To many Pythagoreans this concept meant that things are measurable and commensurable or proportional in terms of number—an idea of considerable significance for Western civilization. But there were also attempts to arrange a certain minimum number of pebbles so as to represent the shape of a thing—as, for instance, stars in a constellation that seem to represent an animal. For the Pythagoreans even abstracted things “have” their number: “justice” is associated with the number four and with a square, “marriage” with the number five, and so on. The psychological associations at work here have not been clarified.

The harmony of the cosmos

The sacred decad (the sum of the first four numbers) in particular has a cosmic significance in Pythagoreanism: its mystical name, tetraktys (meaning approximately “fourness”), implies 1 + 2 + 3 + 4 = 10; but it can also be thought of as a “perfect triangle.”

Speculation on number and proportion led to an intuitive feeling of the harmonia (“fitting together”) of the kosmos (“order of things”); and the application of the tetraktys to the theory of music (see below Music) revealed a hidden order in the range of sound. Pythagoras may have referred, vaguely, to the “music of the heavens,” which he alone seemed able to hear; and later Pythagoreans seem to have assumed that the distances of the heavenly bodies from the earth somehow correspond to musical intervals—a theory that, under the influence of Platonic conceptions, resulted in the famous idea of the “harmony of the spheres.” Though number to the early Pythagoreans was still a kind of cosmic matter, like the water or air proposed by the Ionians, their stress upon numerical proportions, harmony, and order constituted a decisive step toward a metaphysic in which form is the basic reality.

The doctrine of opposites

From the Ionians, the Pythagoreans adopted the idea of cosmic opposites, which they—perhaps secondarily—applied to their number speculation. The principal pair of opposites is the limit and the unlimited; the limit (or limiting), represented by the odd (3,5,7,...), is an active force effecting order, harmony, and “cosmos” in the unlimited, represented by the even. All kinds of opposites somehow “fit together” within the cosmos, as they do, microcosmically, in an individual person and in the Pythagorean society. There was also a Pythagorean “table of ten opposites,” to which Aristotle has referred—limit-unlimited, odd-even, one-many, right-left, male-female, rest-motion, straight-curved, light-darkness, good-evil, and square-oblong. The arrangement of this table reflects a dualistic conception, which was apparently not original with the school, however, or accepted by all of its members.

The Pythagorean number metaphysic was also reflected in its cosmology. The unit (1), being the starting point of the number series and its principle of construction, is not itself strictly a number; for, to be a number is to be even or odd, whereas, in the Pythagorean view, “one” is seen as both even and odd. This ambivalence applies, similarly, to the total universe, conceived as the One. There was also a cosmogonical theory (a theory of the origins of the cosmos) that explained the generation of numbers and number-things from the limiting-odd and the unlimited-even—a theory that, by stages unknown to scholars, was ultimately incorporated into Plato's philosophy in his doctrine of the derivation of sensed realities from mathematical principles.

Mathematics and science

Pythagorean thought was scientific as well as metaphysical and included specific developments in arithmetic and geometry, in the science of musical tones and harmonies, and in astronomy.

Arithmetic

Early Pythagorean achievements in mathematics are unclear and largely disputable, and the following is therefore a compromise between the widely divergent views of scholars.

In the speculation on odd and even numbers, the early Pythagoreans used so-called gno-mones (“carpenter's squares”). This procedure—which was so far Pythagorean—led later, perhaps in the Platonic Academy, to a speculation on “polygonal” numbers.

Probably the square numbers of the gnomons were early associated with the Pythagorean theorem (likely to have been used in practice in Greece, however, before Pythagoras), which holds that for a right triangle a square drawn on the hypotenuse is equal in area to the sum of the squares drawn on its sides; in the gnomons it can easily be seen, in the case of a 3,4,5–triangle for example, that the addition of a square gnomon number to a square makes a new square: 32 + 42 = 52, and this gives a method for finding two square numbers the sum of which is also a square.

Some 5th-century Pythagoreans seem to have been puzzled by apparent arithmetical anomalies: the mutual relationships of triangular and square numbers; the anomalous properties of the regular pentagon; the fact that the length of the diagonal of a square is incommensurable with its sides—i.e., that no fraction composed of integers can express this ratio exactly (the resulting decimal is thus defined as irrational); and the irrationality of the mathematical proportions in musical scales. The discovery of such irrationality was disquieting because it had fatal consequences for the naive view that the universe is expressible in whole numbers; the Pythagorean Hippasus is said to have been expelled from the brotherhood, according to some sources even drowned, because he made a point of the irrationality.

In the 4th century, Pythagorizing mathematicians made a significant advance in the theory of irrational numbers, such as the-square-root-of-n (√n), n being any rational number, when they developed a method for finding progressive approximations to √2 by forming sets of so-called diagonal numbers.