(Static -vrs- Dynamic Equations)
10
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021

Looking at alternative landscapes of thought processing may be useful or simply a dead-end, yet detours are sometimes valuable assets in illustrating a cumulative map as a surveying tool. Regional surveys for the purpose of determining which mathematical tool is best suited for a given strategy of analysis can be helpful in any subject... we need only alter the language of application to the respective research interest... be it mapping out a site for an Anthropological dig, the blueprint field for developing a spaceship or automobile, or in the construction of a tree house for one's children... if not a garden or graveyard plot... as well as a battlefield, proposed neighborhood park, dog run, etc...

However, it should be noted that I am pursuing a trail that some readers might recognize as an idea which (at the very least) suggests an attempt to supersede mathematical inquiry, description, and some formative equation... if not perhaps even the basic contemplations thereof by way of dissecting mathematics to reveal overlooked flaws that can be found in the thinking of other subjects as well. While one can agree that we can think of mathematics as a lingua-franca for all subjects, yet what is beyond mathematics if it is like Latin or other language that has fallen (mostly) out of use?
One such language is that found in chemistry, though math equations can be viewed as expressions of both static and dynamic processes. Such a language is called Dynamic Equilibrium. It can be differentiated from Static Equilibrium. However, different subjects can differ in the way they interpret, define and illustrate what they mean by Dynamic equilibrium. The idea of dynamic equilibrium, like mathematics, can be applied to any subject, be it Sociology, sports science, gaming, economics, political science, Anthropology, art, music, Architecture, Physics, gardening, maintenance operations, etc.. For example:
A system in dynamic equilibrium will have small changes that sum together to produce no net change. Many biological systems are in dynamic equilibrium, from the water inside a cell, to the dynamic equilibrium experienced by populations of predators and prey. Dynamic equilibrium is different from a static equilibrium, in which the parts do not move once they’ve reached equilibrium.
Dynamic equilibrium has different meanings in each science sub-discipline, such as biochemistry or ecology. In chemistry, the equilibrium of a reaction is the point at which the products and reactants have the lowest free energy. The dynamic equilibrium, on the other hand, is the point at which products are being generated as fast as they are falling apart. This may not be the same as the chemical equilibrium, as enzymes force many reactions far past their natural equilibriums by making products faster than they break apart. Due to this, chemist often refer to dynamic equilibrium as a dynamic steady-state, to clearly differentiate between the two points in a reaction.
Ecologists and population biologists will often refer to dynamic equilibrium when talking about populations of organisms. When studying the number of organisms in a population over time, many factors affect the growth of a population. Often, populations will go through periods of boom and bust. Ample resources cause high reproduction rates in all animals, leading to a much higher population. When the resources are distributed among this higher number, there are not nearly enough resources to go around. Thus, the population dies off. Ecologist see these cycles as a dynamic equilibrium that the population is stuck in, never really gaining or losing large numbers of individuals.
Dynamic Equilibrium

What Is Dynamic Equilibrium?
However, the problem with the standard formula for defining a system in which a dynamic equilibrium can occur, is an act of rigging a circumstance in which certain criteria can and will comply... much like the rigged system of performing math equations in a given way. It is an imposed artificiality which offers humans a measure of control and predictability, out of which can be derived a hierarchical social structure... or positioning of people into given slots... as a type of bracketing or parenthetical association denoting a specificity.
Dynamic equilibriums typically derive their definition from the application or interaction of at least two substances and/or conditions, while other variables frequently become overlooked such as time, distance and placement within a larger system such as a chemical reaction taking place in a jar is occurring in a particular room inside a particular building on a particular planet, in a particular solar system etc...
In many instances, we think of equilibrium systems involving three criteria such as Pythagoras' Theorem of A2 + B2 = C2. In other situations we turn to the adoption of dichotomies such as are expressed in the Yin/Yang philosophy, where the idea of a Balancing Act is the terminology used instead of 'Equilibrium'.
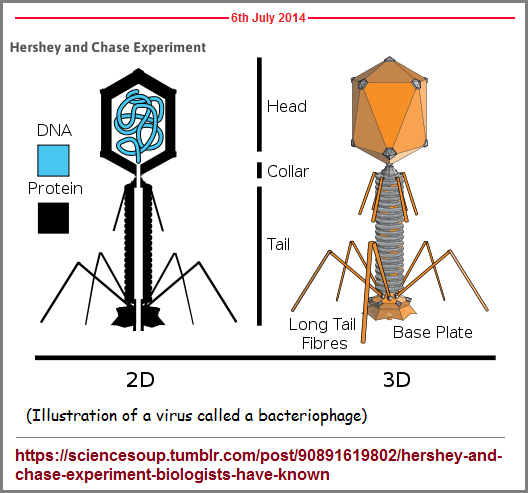
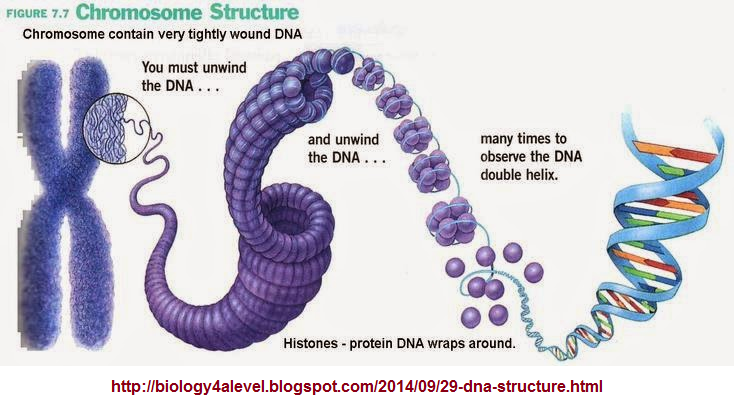
Whether we discuss three categories of learning styles: visual- auditory- tactile (Unlearning the learning styles) By Don Lincoln, Ph.D., August 27, 2020, or The Big Five Personality Traits By Kendra Cherry (Reviewed by David Susman, PhD), on February 20, 2021; one list after another list from one subject to another, are all expressions of a recurring "mathematically-linked" behavior of conservatism which we can otherwise describe as an equilibrium, whether that equilibrium is based on opposition, irritation, hunger, pain, sorrow, absence, or some other difference which is or is not being measured accurately or at all. We can also cite the triplet code of DNA as a balancing act, the 26 letters of the English alphabet as being in equilibrium, the 118 elements in the Periodic Table (which use a "mystical seven" format of display), and multiple other types of lists which... even if suggesting an infinity, are themselves a group of conserved expressions about infinity. In other words, ideas encapsulating the perspective of infinity are themselves few in number. There are not an infinite amount of references to infinity. In more colloquial terms, the lists (equilibrium systems) are short... just like the groups of axioms we see in mathematics. They are meant to provide an equilibrium based on some supposed logic, but that logic is flawed. We are attempting to... but falling short of... packing more and more information into smaller criteria (like actively engaging in making systems of equilibrium more condenses as if to create a rare gem of thought... like those pressures used to create diamonds); just like some compartmentalizations seen in prokaryotic DNA replication and tightly packaged genetic material in the linear chromosomes of a prokaryotic genome as well as the compression of DNA in the genome of bacteriophages. Whereas we see triplet strands being compressed, we do not see quadruple, quintuplet, sextuplet, etc. strands. Neither the quantity of strands nor the quantity of sub-atomic particles are "growing"... or going towards a complexity. The count, the quantity... is conserved... as if some environmental effect(s) (events) are acting as a form, a model, a sort of cookie-cutter to minimize the expression(s) in a repeating pattern.
Take any subject, including mathematics, and you will pay witness to an ongoing expression of cognitive conservation suggesting an equilibrium of cognitive functioning has been achieved and thus should be dispensed to all citizens via a public education system like an enforced inoculation program to remove some supposed disease that arises without it.
Conservation law, also called law of conservation, in physics, a principle that states that a certain physical property (i.e., a measurable quantity) does not change in the course of time within an isolated physical system. In classical physics, laws of this type govern energy, momentum, angular momentum, mass, and electric charge. In particle physics, other conservation laws apply to properties of subatomic particles that are invariant during interactions. An important function of conservation laws is that they make it possible to predict the macroscopic behaviour of a system without having to consider the microscopic details of the course of a physical process or chemical reaction.
- Conservation of energy implies that energy can be neither created nor destroyed, although it can be changed from one form (mechanical, kinetic, chemical, etc.) into another. In an isolated system the sum of all forms of energy therefore remains constant. For example, a falling body has a constant amount of energy, but the form of the energy changes from potential to kinetic. According to the theory of relativity, energy and mass are equivalent. Thus, the rest mass of a body may be considered a form of potential energy, part of which can be converted into other forms of energy.
- Conservation of mass implies that matter can be neither created nor destroyed—i.e., processes that change the physical or chemical properties of substances within an isolated system (such as conversion of a liquid to a gas) leave the total mass unchanged. Strictly speaking, mass is not a conserved quantity. However, except in nuclear reactions, the conversion of rest mass into other forms of mass-energy is so small that, to a high degree of precision, rest mass may be thought of as conserved. Both the laws of conservation of mass and conservation of energy can be combined into one law, the conservation of mass-energy.
- Conservation of linear momentum expresses the fact that a body or system of bodies in motion retains its total momentum, the product of mass and vector velocity, unless an external force is applied to it. In an isolated system (such as the universe), there are no external forces, so momentum is always conserved. Because momentum is conserved, its components in any direction will also be conserved. Application of the law of conservation of momentum is important in the solution of collision problems. The operation of rockets exemplifies the conservation of momentum: the increased forward momentum of the rocket is equal but opposite in sign to the momentum of the ejected exhaust gases.
- Conservation of angular momentum of rotating bodies is analogous to the conservation of linear momentum. Angular momentum is a vector quantity whose conservation expresses the law that a body or system that is rotating continues to rotate at the same rate unless a twisting force, called a torque, is applied to it. The angular momentum of each bit of matter consists of the product of its mass, its distance from the axis of rotation, and the component of its velocity perpendicular to the line from the axis.
- Conservation of charge states that the total amount of electric charge in a system does not change with time. At a subatomic level, charged particles can be created, but always in pairs with equal positive and negative charge so that the total amount of charge always remains constant.
- In particle physics, other conservation laws apply to certain properties of nuclear particles, such as baryon number, lepton number, and strangeness. Such laws apply in addition to those of mass, energy, and momentum encountered in everyday life and may be thought of as analogous to the conservation of electric charge. (See also symmetry.)
- The laws of conservation of energy, momentum, and angular momentum are all derived from classical mechanics. Nevertheless, all remain true in quantum mechanics and relativistic mechanics, which have replaced classical mechanics as the most fundamental of all laws. In the deepest sense, the three conservation laws express the facts, respectively, that physics does not change with passing time, with displacement in space, or with rotation in space.
This article was most recently revised and updated by Erik Gregersen, Senior Editor: Conservation Law (Physics)
the above article by the Britannica illustrates conservation in that it does not speak of the conservations taking place in other subjects because such an idea is not commonly considered. For example, the triplet code of DNA can be considered an expression of Conservation. In mathematics, its rule and processes for completing an equation are an expressed conservation just as are the limitations of application. Whereas one person might think that mathematics is not conserved because they use the terms "universal application on all subjects materials", they do not describe the so-called "many" subjects of humanity in the real terms of being a conserved quantity. Other examples include the conservations regarded as limits frequently seen in repetitions as well as the limitations seen in athletic events: The limits of human athletic performance (by R J Maughan), or Cognitive limits (by Maarten Boudry), while the idea of Matching Human Abilities and Limitations (by David Kieras), fails to take into consideration the ongoing incremental deteriorations of the planet and its relationship with the Moon and Sun. Far too often the human brain thinks of the human species in geological duration terms and not those terms of existence related to the species humanity presently is, which I believe are more intune with the life cycle of the fruit fly (Drosophila melanogaster) or other short-duration species in terms of adaptation and life cycle. (Fruit Flies First Began Feeding on Our Fresh Produce About 10,000 Years Ago by Jason Daley, Smithsonian Mag.com, Dec. 7, 2018).

A more detailed image: The Relative Size of Particles
But why do we compartmentalize if it too is not part of an unrecognized environmentally influenced behavior on biology to reduce and symbolize, as if we are constrained in our ability to spread our wings... so to speak? Why only zero through nine in our numbers list? Why do most people not recognize that our multiple types of lists are conserved? Why so often do we find a reductionist approach which eventually compartmentalizes information into a quantifiable set that very frequently exhibits recurring amounts such as one, two, and three, or 4, 5 and six, or 7, 8 and nine... all of which express three-patterned ensembles, but since the word "ensemble" is not customarily used outside of jewelry or clothing, the frequency of using "set" in mathematics in a particular way excludes most people from realizing the presence of the ongoing conservation which appears to be headed towards more conservation... but language and "complexifications" of the conserved material creates the illusion and delusions of something greater than it is... because the human ego relishes such a mirror image? Why don't mathematicians see the ongoing conservation taking place in mathematics and that its language is an expressed conservatism that is not seen as a tell-tale sign of an encroaching environment with its ongoing incremental deteriorations? Why don't mathematicians recognize their behavior as a BEHAVIOR just like any behavior being seen in different life forms such as hibernation in bears, nest building by birds, termite mounds, ant-lion burrows, fight-flight-freeze responses, etc...?
Mathematics is like a spider web created by a spider unaware that the environment in which a spider can produce their web is slowly being reduced. Mathematicians do not see the web being altered by a reductionist change in the environment. That is, reductions not only induced by an increasing population, but by decreasing irreplaceable resources in the environment. While some resources are replenishable if given enough time and no interference, conditions on Earth because of an increasing population do not allow for the time needed by such resources. The state of mathematics is showing us the future, but too few mathematicians reach the level of mathematical understanding which enables them to see mathematics as a behavioral expression of a biological circumstance in a deteriorating environment. Even though mathematics has exhibited the characteristics of organisms adapting to a wide range of environments, it is not typically investigated as an organism even though it portrays many patterns of survival efforts such as becoming predatory in many instances, while in others it has become more passive and routinely docile such as a domesticated animal. While different approaches to the types of mathematics being used in a given setting can be used, it is helpful to look at those found in biology and other subjects as a means to provide some ideas. The following abstract about the study of spiders in Chile is such an example... and is not being used to express some definitive application of effort with respect to the current subject. However, one should note the "three" criteria being outlined whereas in other research efforts the "three" may be expressed in terms of length of time, number of subjects, the quantity of researchers, and is a recurrence which some readers may want to defend through some practiced rationalization such as cost, necessity, etc...
Abstract
Spiders are small arthropods that have colonized terrestrial environments. These impose three main problems:
- Terrestrial habitats have large fluctuations in temperature and humidity;
- The internal concentration of water is higher than the external environment in spiders, which exposes them continually to water loss;
- Their small body size determines a large surface/volume ratio, affecting energy exchange and influencing the life strategy.
In this review we focus on body design, energetic, thermal selection, and water balance characteristics of some spider species present in Chile and correlate our results with ecological and behavioral information. Preferred temperatures and critical temperatures of Chilean spiders vary among species and individuals and may be adjusted by phenotypic plasticity. For example in the mygalomorph high-altitude spider Paraphysa parvula the preferred temperature is similar to that of the lowland spider Grammostola rosea; but while P. parvula shows phenotypic plasticity, G. rosea does not. The araneomorph spiders Loxosceles laeta and Scytodes globula have greater daily variations in preferred temperatures at twilight and during the night, which are set to the nocturnal activity rhythms of these species. They also present acclimation of the minimum critical temperatures. Dysdera crocata has a low preferred temperature adjusted to its favorite prey, the woodlouse. Spider metabolic rate is low compared to other arthropods, which may be associated with its sit and wait predatory strategy particularly in primitive hunter and weavers. In mygalomorph spiders the respiratory system is highly optimized with high oxygen conductance, for example G. rosea needs only a difference of 0.12–0.16 kPa in the oxygen partial pressure across the air-hemolymph barrier to satisfy its resting oxygen consumption demands. Water loss is a significant stress for spiders. Paraphysa parvula shows an evaporative water loss 10 times more than usual when the temperature approaches 40°C and the participation of book lungs in this loss is about 60%. This species and others show seasonal changes in water loss accounted for by changes in cuticle permeability. The case of Chilean spiders shows how the ecophysiology in spiders is associated to their design and body size and how is affected by fluctuating Mediterranean environments, suggesting that the adaptive process can be seen as a route of optimizing the use of energy to cope with environmental restrictions imposed by the interaction with the terrestrial environment and lifestyle.
Adaptation of the spiders to the environment: the case of some Chilean species by Mauricio Canals, Claudio Veloso, and Rigoberto Solís
3 Examples of "three" usage in different spider studies:
- Analysis of Body Size, Web Size, and Diet in Two Congeneric Orb-Weaving Spiders (Araneae: Araneidae) Syntopic in Florida Scrub by James E. Carrel and Mark Deyrup; (assigned them at random into 3 treatment groups)
- Studies on the Geometrical Design of Spider Webs for Reinforced Composite Structures by Yohannes Regassa, Hirpa G. Lemu,Belete Sirabizuh and Samuel Rahimeto; (There are three general stages that all types of data have to undergo when using a digital image processing technique.)
- Scientists Translated Spiderwebs Into Music, And It's Beyond Stunning by Michelle Starr, 13 April 2021; (Many studies focus on the 3-dimensionality of spider webs, contrasting it with 2-dimensionality.)
A much simpler idea is conveyed by visualizing the The Mechanics of Spider-Webs from the perspective of incrementally placing a spider in smaller (more compact) environmental settings in order to determine whether the web will be subjected to a similar "down-sizing" and exhibit a less complex, more compact, or simply a 'pygmy' version of its typical outline. Then again, if a given spider is born with an innate blueprint (or paper bag sketching) of how to construct a given web, does the blueprint have a set requirement of space, elevation, etc., such as a contractor determining a given build-design by the amount of land that is available? Do spiders actively seek out a terrain with attachment points which correspond to some internalized math/geometry plan? If mathematics is a web and spiders are akin to spiders, will not the web(s) exhibit a change over time if the spider is subjected to an incrementally deteriorating environment? This is in fact what I am trying to convey... that mathematics is displaying the ongoing incremental deterioration of the Earth in its relationship to the Sun and Moon. The Sun's energy is depleting, the Moon is moving away and the Earth's rotation is slowing. The structure of Mathematics is exhibiting the deterioration because Mathematicians are experiencing an increased constraint due to lessening space and other resources.
 |
 |
 |
As environmental constraints continue, will the impact on mathematics be similar to changes in spider webs? Whereas it is thought that mathematics will adapt in "mathematically"-related ways, what if it doesn't? Can we predict what different ways in which mathematics might respond to a changing environment? | ||
If a spider has a built-in blue-print of the design and size a web is "supposed" to be, will the design and/or size change if the environment gets smaller? Is the web of a spider in a small jar just a miniaturized version of that in a much larger jar? And if other variables in the environment change, is the web altered accordingly? Is there an environmental-specific element which determines size or design and complexity of the design? Since we are seeing the same type of math being executed, does this mean the size of the jar is the same... or mathematics as it is being taught determines the constraints? Is there a limit to the complexity of a spider web and thus also to mathematics as it is being practiced? If the vibrations of a web is akin to dynamics, how then do we "feel" or sense the dynamics of a math equation portrayed along a linear path if mathematicians are not aware of how or that they are able to detect the dynamical nature of mathematics... unless the linear equations are too inflexible and cannot vibrate.

One must wonder whether a spider has a picture of a web in its brain (or simply, genes), or if they are sensing vibrations in the environment which act as bumper guards and search light illuminations? In other words, is a spider web a blueprint, or an act of chiseling out a form from the raw matter of the environment which is emanating signals in a particular pattern?
Viewing a math equation as a spider web, the usage of linear equations suggests single "streamers" and do not admit to any geometry as might one think in terms of a circle, square, triangle, etc... Like many a spider who hangs from a single thread of web, mathematicians are engaged in the usage of linear equations which are part of a larger web of available applications, but to not traverse the 'ground' of the larger web with its vibrating intricacies of potentiality.
Environmental effects on spider webs might well be more easily understood by looking at An old NASA study gave spiders drugs to see how it affected their webs:
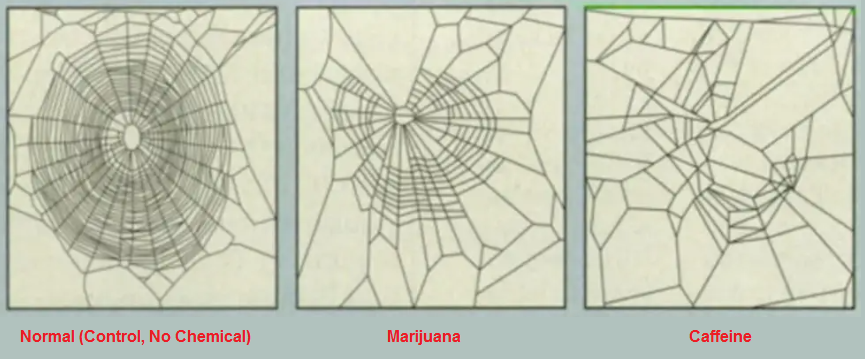
While mathematics has been undergoing a dynamic alteration, Mathematicians are still viewing it in terms of a linear and static (routine) conveyance of ideas. It is much like someone being born on a ship and having lived many years adapting to the wave patterns, only to find their equilibrium is off when first stepping onto land. They still have their "sea legs" within the framework of their minds (and body), while navigating an existence on dry land. (Or one can flip this view around and say that Mathematicians have (static) land legs in their mental preoccupations while trying to navigate more dynamic environments.) Mathematics is like a gyroscope aligned to existence on a static dry land (despite geological instabilities), that is being applied as a tool-of-habit on a dynamic sea. If we also add the environment of space to the equation, the gyroscope that was altered for life in an assumed static environment must again be altered. However, the human mind clings to old ways of thinking and has difficulty making the change from its static orientations to those dynamic orientations of sea, space, time, gravity, energy, evolution, etc., though mathematical models suggest the existence of such.
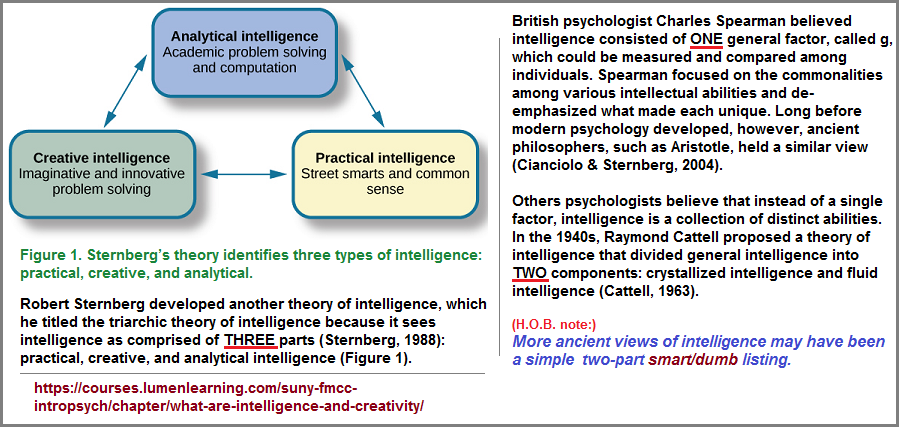
Many Mathematicians or those who play chess well or those who can perform a Rubics' cube problem in a quick manner, consider themselves to be uncommon with respect to their intelligence. So let us take a look at the study of intelligence and note that it too, like so many other subjects, expresses a one, two, three formula found also in the babbling behavior of infants... from which a multiplicity emerges.
Date of Origination: 26 February 2021... 6:59 AM
Initial Posting: 1st July 2021... 4:45 AM