Threesology Research Journal

"Infinitesimal versus Accordian Calculus"
(Static -vrs- Dynamic Equations)
3

~ The Study of Threes ~
http://threesology.org

---

Visitors as of 2/27/2021

If you have been trained in the use of an abacus, being presented with an electronic calculator may be rejected. Though the numbers and some of the symbols may be familiar and you come to familiarize yourself with being able to use a calculator for simple arithmetic equations, the other displayed functions may well appear to be a foreign language, just as an explanation thereof may appear to be too weird and inapplicable to the conventions of thought you are accustomed to. By being named a dynamic equation in contrast to a static equation, one is enabled to get a bearing on the proposed journey ahead. No doubt some ideas will be quite familiar, as they should be, but are now seen from a different vantage point. For example, a person who in their daily life uses a measure of Algebra without realizing they are doing so, can more easily be introduced to the task of Algebraic equations by having their own thought processes being given a name, a label for the establishment of an identity with which to personalize efforts and recognize other Algebraic functionalities that others may be engaged in, and share in a similar journey of exploration. Providing a name, a label to a type of mental logistics... enables a person to begin a step-wise direction along which they can mark out a trail of accomplishment and/or the realization of a false lead if not a dead end. By establishing an identity, a type of thinking can be formalized out of its feral antics of expression so as to provide recognizable stepping stones that everyone can see and choose to step on or say: "Hey Wait up! Why don't we try this way along this path where fallen leaves give the impression of a Natural path?" To which one might reply: "I've been there already." or: "That's a good idea!" or: "Well, why not?, I'm game."

• 8 Historical Figures with Unusual Work Habits
• Ten odd obsessions of famous philosophers
  
  
  1. Rene Descartes: Youthful passion for cross-eyed ladies (It is said that Descartes used his free will to rid himself of this so-called irrational attraction... In other words, he psychoanalyzed himself and applied a treatment to what he considered was an irrationality.)
  2. Albert Camus: Fear of an early demise created an obsession with death in general.
  3. Immanuel Kant: Rigid Schedule (The path Kant walked was later named the Philosophengang, or "The Philosopher's Walk". A Philosophy of Walking: Thoreau, Nietzsche and Kant on Walking.)
  4. Soren Kierkegaard: Family curse... Kierkegaard believed he was cursed and that God would take his life at an early age.
  5. Karl Marx: Frantic idea Generation... Marx's inner chaos is exemplified by the compulsive manner he generated ideas.
  6. Friedrich Nietzsche: Obsession with fruit to combat medical issues.
  7. Voltaire: Constant Need for coffee (caffeine junky?)
  8. Georg Wilhelm Friedrich Hegel: His favorite clothes (nightgown and black beret).
  9. Jean-Paul Sartre: Obsessive fear of crustaceans and other sea creatures.
  10. Arthur Schopenhauer's pessimism and personality led him to fill his human need for companionship with pet poodles.
• "I would not dare to say that there is a direct relation between Mathematic's and madness," said the mathematician John Nash, "but there is no doubt that great mathematicians suffer from maniacal characteristics, delirium and symptoms of schizophrenia." Nobel prize winner, mathematical maverick and schizophrenic, Nash is one of the high-profile mathematicians whose life-story, portrayed in the film A Beautiful Mind, contributes to the popularly held belief that there is a link between genius and madness. The Madness Of Mathematic's by Timothy Bano, 24th May 2012
• Alexander Grothendieck was among the greatest mathematicians of the 20th century, until he withdrew from the world. Neuroscience may finally shed light on why epoch-changing minds make drastic midlife turns. The Mad Genius Mystery by Kaja Perina published July 4, 2017

Let us ask: Are we confronted by only a handful of geniuses in Mathematic's are all of them a bit mad? Then again, perhaps most are just those who remain in touch with the "inner child" and search within the field of Mathematic's to pursue a perpetual means of playing games, such as treasure hunting, chase, or follow the leader; which appears to represent much of what mathematicians do with respect to equation repetition... and an inability by some to proceed past their particular game of hopscotch or pin-the-tale-on-the-donkey. The following are two views on the idea of "follow-the-leader" (American version), or the British variety of "follow-my-leader". The first view illustrates the common theme (or at least used to be a common children's game before the advent of electronic's games), and the second image indicates what becomes of those adults who have not learned how to step outside the cognitive maps of childhood and pursue like-minded adult activities that may have disastrous effects not only for individuals, but the entire species if we are permitted such an application thereof. Let me also add that when someone reaches an age... a moment in their life when they reflect on where they are and want to break away from their routine, they usually do so in a way that others have also chosen, whereby they are playing another type of follow-the-leader, albeit perhaps with fewer players in an unfamiliar place performing unfamiliar activities which give a sense of having broken free from the chains of their previous life's routine... which in many cases is enough for them.

Then again, it is said that misery loves company and that both become spectators and participants in sustaining the atmosphere in which the misery occurs... typically in familiar surroundings; like couples who have come together in a given circumstance and cannot relate to one another in another way. Such is the case we may find when linear and dynamic equations come to meet and if they do not mate, then they separate and carry on in their separate lineages, whether or not substantial changes take place as in an evolutionary sense.

Follow the Leader (game)

Follow the Leaders by Isaac Cordal (sculptures exhibition)

Before going too far in the present discourse, let me briefly state that the present endeavor is not part of the old "Calculus Curriculum Reform" where emphasis for WHAT is being taught as a dichotomy to HOW it is being taught and the two are intermixed with varying levels of student participation... all of which gives the impression of using Calculus as a subject by which a trial-and-error process for the practice of an enlarged model of Democracy can be undertaken and yet remain concealed from socio-political philosophers who would take issue with anyone stepping over the line into their claimed domain in which they generate some measure of personal fame and that no one, especially math students, can possibly have the intellectual acumen for creating a better model of government without their say so and added-in two or more cents worth of agreement. My feelings and thoughts are that the present model of not only Calculus but many equations, are too static, despite the claim that Mathematic's is said to be a very vibrant, moving and "visual" activity. Whereas maybe it is quite visual and quite dynamic for thousands of people who are not as visual or mentally dynamic as they think they are; it goes without saying (yet I still say it) that we need a more dynamic form of Mathematic's (or beyond mathematical activity) for those who have an over-average capacity of visualization and memorization which is unique to a different model of perspicuity. A case in point might said to be the present day interpretation of the early life-story of Srinvasa Ramanujan:

The life and story of Indian Mathematic's Genius Srinivas Ramanujam provides an unique example of SDL (Self Directed Learning). Srinvasa Ramanujan was born on Dec.22, 1887. He had his primary education on Verandah of a Primary school, in Kumbakonam, a village in Tamilnadu, India. The student is made to recite a collection of vedhic verses to develop their mnemonic ability. This process of recitation help them indirectly develop logical thinking and reflective introspection. The students were made to recite the number, vocalize it, and draw it on a medium. This process helped them to inculcate the habit of vocalization, visualization and memorization. This is named as re-collective memory. Ramanujan developed his interest in numbers in the verandah of primary school. In his school, education among the different subjects that are taught to him as a part of the syllabi, Mathematic's become the subject of his interest. Numbers fascinated him, theorems, formulae become the alphabets of his learning. His innate ability to learn and master pure Mathematic's made him devour the contents of Mathematic's text books of higher standards. He mastered them easily. He spent all his time recording in his own handwriting the problems, prime numbers, solutions and theorems in diaries. He had three such diaries which had all his research work on different aspects of pure Mathematic's. He had great desire to learn Mathematic's and search for highest form of truth about the world through mathematical language. His research was inborn, had reference to any other research papers or books or teachers to help him carry forward his journey in the realm of Math. His obsession for Mathematic's was so great he never gave attention to the learning other subjects. This acted against him to qualify or get a degree in a college. The letter he wrote to Dr. Hardy, UK stands as a proof of his inherent genius:

"I have had no university education but I have undergone the ordinary school course. After leaving school I have been employing the spare time at my disposal to work at Mathematic's. I have not trodden through the conventional regular course which is followed in a university course, but I am striking out a new path for myself. I have made a special investigation of divergent series in general and the results I get are termed by the local mathematicians as 'startling'".

The example of Ramanujan's learning opens up a fresh idea that the syllabi need to be flexible and the freedom to make a choice of learning that interests the learner. The learning capacity of an individual has to be nurtured in an environment which provides that freedom of learning. Rather learning must be spontaneous and self-reliant. For such a learning the mind must be fertile, fresh and unpolluted by instruction of a formative education or any other form of instruction.

"Education is not to reform students or amuse them or to make them expert technicians. It is to unsettle their minds, widen their horizons, inflame their intellects, teach them to think straight, if possible." - Robert M. Hutchins

Ramanujan: A Role Model for Self-Directed Learning (SDL)- A Perspective by Dhastagir SultanSherif

To the foregoing, one must ask why there aren't more Ramanujan-like individuals coming out of present programs of early education using the methods thought to be responsible for the development of Ramanujan's type of thinking? Granted he grew up on a diet devoid of the many forms of electronic distractions kids today have, but is there something everyone is missing in the attempted interpretations of what environmental events assisted him in his development? Is it a unique quality of memorization? Visualization? Both? Neither? Different approaches might be scrutinized such as the following idea that may or may not have merit for one or another reader who would think alternatively:

While many review the life of Ramanujan... thinking that more people like him can be brought into existence if they are subjected to a similar life style, educators find this is not the case. While the conditions under which a given genius is eventful for them, it is not necessarily true for anyone else with their specific genetics and age into which they are born. Then again, the so-called great accomplishment(s) of a genius, be it an Einstein, Da Vinci, Ramanujan or someone else you admire, may only be defined as being great or significant for those who share in the same type of thinking and are permitted to exercise this view upon the public to be reinforced by others to agree with them... and yet the work or works of the declared genius have no impact on the life of the common person. It is like a sport where some player performs some deed interpreted by other players as being unique and one-of-a-kind; but has not real value for anyone outside that particular sport, though there may be several people outside the inner-circle of the sport's culture who admire the actions and adopt a certain perspective of reality which they think reflects the sports world in which they are envious of its players and their lifestyle. This is mathematics. This is Biology. This is Chemistry, Medicine, Anthropology, etc... While some "sports" like music are more wide-spread amongst the public than say Chemistry as it is practiced in laboratories, it still is its own reality.

The present forms of Mathematic's, if indulged in, only force such visualizers to agree with the perspective... with the illusions of those who have difficulty seeing beyond the proverbial-stated fingertips to the dawn of a new horizon emerging in the recesses of a type of brain functioning to be found in multiple other-than-mathematical interests; where a different model of dynamic Mathematic's is practiced because current models of Mathematic's doesn't even know it exists. In other words, dynamic forms of mathematical-like thinking exist in other subjects but that those participating in the usage thereof may not even be aware that they are expressing an advanced formula of thought. It is like placing a Neanderthal, Cro-magnon, and Denovian together in a room having a casual conversation, but the underlying mental processes of all three is somewhat different in how they perceive reality but may be unable to accurately describe it because the realization of such is not a customary part of discussion nor even been given a label to effectively reference as a topic of discussion, even though it exists as an active functionality as part of a brain that is evolutionarily different... though some readers may prefer to say superior because it makes them feel better about themselves.

If we view Mathematic's as a type of "zone", just as we might any subject... be it focused on some physical or mental effort (with or without emotion), I am thus speaking about the development of a zone beyond the Mathematic's zone... or if you prefer: the Mathematic's dimension. What type of conceptualization lays beyond Mathematic's? Is it felt to be the last frontier... the Queen of conceptualization to be surmounted by art, music or some other routine claim, or is their a "zone" with a territorial vista which will use Mathematic's as a surveyor's tool by which to construct a more enlightened edifice whose blueprint acknowledges the contributions of math, music, art, etc., but must recognize them for their respective uses as we do different types of dishware, cutlery and junk drawer ensemble we use from time-to-time and need ready access to? If memorization is said to be important, and that which is being memorized is a necessary value, then if we adopt a different type of memorization and that to be memorized, what have we thus created in our wake of pursuing such an idea, such an animal, such a creature whose appearance and behavior may be familiar, but either taken for granted or thought too conventional to be given much regard for further analysis, because it is otherwise defined as most do when surveying a field of flowers, a forest of trees, a desert sand dune, or wintry landscape? How do we possibly recognize a unique zone of possibility if it is like a hole most people step over and create varying labels for which amount to some reason for aversion or other-styled avoidance... like the many who, in the past, discarded bones and artifacts at what we today would define as an important Archeological and Anthropological site? Are Mathematicians too arrogant, too lost in their respective zones to recognize or accept the possibility that there may be a zone beyond mathematic's?

If necessary, the arrogance of the self-proclaimed "queen" of all subjects needs to be humiliated in such a way as to force her into a greater objectivity by way of a long-overdue humility which casts her into a mood of reflectiveness whereby she is more receptive to alternatives ways of perception within and outside of mathematics that is not art, not music, not any conventional alternative disposition, but something altogether new. My intent in the current expose' is to lay the initial step to imprint the ideas of a new trail upon which a different model of calculation... of calculus will emerge... like the present moth of calculus... of cacoon-like equation formation and application; towards becoming a butterfly which is itself transformative beyond this state of existence as well, notably seen as but another type of cacoon out of which to develop from, because each cacoon is a type of zone as well.

Here's an example of mental fluttering one might engage in, so as to present some modicum of what is meant by a linear equation for those readers who may not be able initiate their one visualization thereof, much less think to include alternatively directed orientations with some later age explanation which is an exhibition of some very basic elementary school impressions:

The steps of a butterfly's life sequence used as both an analogy and metaphor for Mathematic's thinking:

When thinking about the life cycle of a Mathematic's form, we do not take into consideration that they may well exhibit a biological expression from birth to brightness to brimming with enthusiasm and then along a course which portrays a slow deterioration and becomes solidified by routines of usage. Indeed, to stop teaching present Mathematic's courses... or any subject's courses, and force the human mind to develop a substitute that outshines the former mental tools... where the adage that Necessity is the mother of invention comes into play. Then again, let us also look at the butterfly analogy and make note of the fact that many expressions of the "cycle' take this very word to heart and create an image resembling a circle, whereas in actual natural surroundings, the 'cycle' expresses more of a linear equation. Hence, we have not model of a circular equation. Likewise when we speak of the Krebs Cycle where "cycle" can alternatively be referred to as a "series" of reactions... where the word "series" may well evoke the image of a linear sequence of events, as opposed to a "cyclical" round image. No less, though we speak of a "bicycle", the word is not a full "equation" (explanation of the object) in that it does not portray the linear motion of the supposed dynamic which the word "cycle" may convey to some readers.

As an interjection (since I began thinking of this several days after writing this section), the idea of cyclicity can include the notions of time as seen on a clock whose hands are constructed to proceed in a "clockwise" fashion (left to right), just are the wheels of all vehicles if viewed from the left side of the vehicle denoted as the front passenger's side. One must consider the possibility that these and other circular ideas are an unconscious attempt by humanity to construct a model of a dynamic thought processing which, in terms of mathematics language is referred to as a circular equation. If such items are to be viewed as rudimentary forms of circular equations... or "drawing board" models expressed in crude... but often embellished structural forms, how is mathematics to convey this underlying impulse to design such, by using static linear equations? Simply using a linear equation to speak of a circular motion is not a dynamical expression. It is little more than a stick figure of an animated form. Likewise, a moving clock does not necessarily accurately describe that which we label as time, since we do not exactly know what time is, if it exists at all beyond human conceptualizations thereof.

What we come to is an attempt to define what is meant by a "dynamic" equation. Does it remain in a static state attempting to describe animation or is itself animated, yet focused on static themes? Are we to simply engage in a philosophical debate about what is meant as being a dynamic equation, only to find ourselves entrapped in yet another industrious philosophical dichotomy which does not recognize itself as being part of a tri-cyclic orientation such as:

• here, there, everywhere
• up, down, in-between
• forwards, backwards, stationary
• left to right, right to left, up/down... diagonal
• major premise, minor premise, conclusion
• near sighted, far sighted, correct/stationary sighted
• minimize, maximize, "mediumize"... centralize
• north/south- east/west, up/down
• time, space, matter
• 1st 3-dimensions, time-dimension- "other" dimension
• solid-liquid-gas, particle-wave-vibration, dark matter-dark energy-dark time/dimension/co-existence
• slide, swing, teeter-totter
• 3 strikes, 4 downs,
• million (1st), billion (2nd), trillion (3rd)
• consciousness, reality, illusion/delusion... confusion
• male, female, androgynous figure
• hot, cold, warm
• yin, yang, unity
• chocolate, vanilla, strawberry ((traditional ice cream flavors)
• small conflicts, medium conflicts, large conflicts
• Mossad (1st), CIA (2nd), (Chinese? Russian? 3rd)
• weak, strong, average...
• mono-furcation?, bifurcation, trifurcation
• one engine (most vehicles), two engines (racing), three engines (space shuttle)
• monofocal, bifocal, trifocal
• unicycle, bicycle, tricycle
• past, present, future
• masculine, feminine, neuter
• dumb, smart, mediocrity
• Uglification, Beautification, Moderation
• paper, rock, scissors
• one, two, many (general theme representing ancient efforts for establishing a tool of measurement called counting)
• existence, non-existence, intermittancy (wavering between existence and non-existence)
• red light, green light, yellow light
• monad, dyad, triad
• integrate, disseminate, disintegrate
• person, place, thing ("mnemonic" for nouns)
• period, question mark, exclamation point
• use 2 fingers to write with, 3 fingers, whole hand (children)
• monomer, dimer, trimer
• single layer, bi-lipid, trilaminar (biology cell/organelle layering)
• 1 germ layer (sponges?), 2 germ layers (), 3 germ layers (from earth worms to humans)
• single stranded, double stranded, triple/quadruple stranded (rarities)
• etc...

Note: if I don't put a sizeable enough list, the reader may think that a list they would compile is thus suggestive of a short listing for this type of configuration leading to a conclusion it could be dismissed because they could think of a list involving some other pattern; yet never take stock of the overall lists which we humans might (but don't) engage in is representative of a conservation. In other words, the length of the lists must be contrasted with the quantity of number lists we would create... thus enabling us to see that even if we put together a list of ones, twos, threes, fours, fives, sixes, sevens, eights, nines, etc..., the numerical value of the totality is extremely small since we use but a small fraction of all available numbers. Likewise, with respect to mathematics, we use only a small fraction of equations which might be produced... since the quantity of equations being used within the restrictive axioms and proofing methodologies creates a conservation and this conservation is labeled with various egocentricities such as logic, truth, reality, etc., all of which are references to human endeavors to create the epitome of intellectual realization.

Is the usage of an arrow a particularly good image of time?... or the usage of a comparative model where we describe it as either a gain or loss? If time is dynamical and it is not subject to being defined in human terms of perception, can we even approximate what it is... or only see it as we observe the wind in terms of leaves blowing, trees bending, and debris whisking about our hair swirling about us? Is time akin to a wind? Or the heat felt by a flame but cannot be "seen" without the aid of instrumentation to visualize such a spectrum? If we say that time can exist as part of the electro-magnetic spectrum or some other as yet unrecognized spectrum of phenomena human consciousness is struggling to conceptualize by adopting one or another label-name from familiar ideas which may be more of a hindrance in the description thereof instead of an asset; will we then be able to construct a dynamical equation model? Or can one simply point to a clock, a wheel, or other circular movement and say it is an artistically rendered dynamic equation... as a reverse of the many mathematical efforts being labeled forms of art using mathematics as the limited palate of colors... not to mention the limited types of brushes and mediums and topics; like an artist whose only "brush" is a ball-point pen and their only medium is notebook paper upon which they sketch out the same bowl of fruit as it withers unsuspectingly?

While some readers will easily be able to visualize the foregoing short list of linear dichotomies/trichotomies into mobile (animated) variations, others will simply see them as a static listing of different ideas involving both dichotomies and trichotomies... depending on what context and who is using such configurations of thought. Some may well visualize them in a triangular configuration while others may pursue quadratic and further enumeration conveyed in geometric figures.

The "cycle" reference can also be interpreted to mean rhythm such as in biological rhythms related to the circadian form, though other rhythms exist (diurnal). Unfortunately, those who are musically inclined take the word "rhythm" to mean a beat or some other attribute conducive to their vocabulary associated with music, and may not lend some of them with an alternative intent of describing the 'rhythms' mathematically. And yet, so very often found among those who do, they turn to describing their model of Mathematic's in musical notation but rarely any connection to external events of rhythm... unless they possess an ability to adopt a generality of application to any and all things being perceived, such as the rhythm of waves in brain waves, electrical waves, solar waves, ocean waves, waves of speech, waves of body functions, waves of light an all other electro-magnetic spectral forms. For the present, let's touch upon the biological form of rhythms as expressed in the following excerpt. (Note, in order to write a dynamic equation, we need lots of different information like the gathering of organelles into a space called a cell which later duplicates and emerges into a sentient being called humans. Present, singular forms of linear equations are too static and required additional layers to represent additional dimensions of activity. For example, one linear equation can be viewed as being one-dimensional, two linear equations as tow-dimensional if they are aligned as such, and three linear equations can be used to express three dimensions if they are organized as such. Simply writing three equations does not make the overall combined expressions representative of three dimensions, irrespective of how much imagination is applied and the resulting portrait is labeled as such.)

While some of you will only see the following article as an expression about biology, I am viewing it as part of the information needed for a dynamic calculus.

J Cell Biol. 2016 Oct 10; 215(1): 15–25.
doi: 10.1083/jcb.201603076
PMCID: PMC5057284
PMID: 27738003

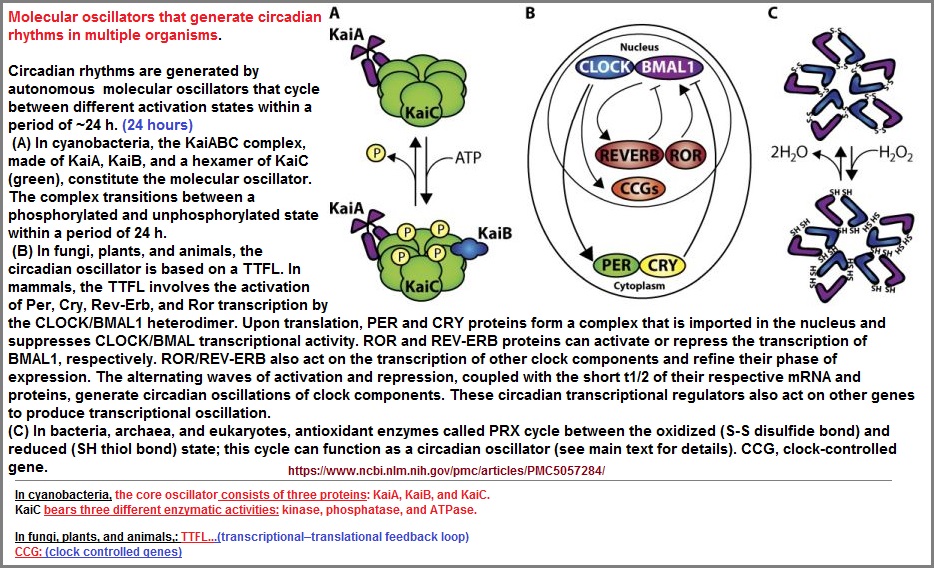
The circadian coordination of cell biology
Amandine Chaix, corresponding author; Amir Zarrinpar; Satchidananda Panda, corresponding author

Abstract

Circadian clocks are cell-autonomous timing mechanisms that organize cell functions in a 24-h periodicity. In mammals, the main circadian oscillator consists of transcription–translation feedback loops composed of transcriptional regulators, enzymes, and scaffolds that generate and sustain daily oscillations of their own transcript and protein levels. The clock components and their targets impart rhythmic functions to many gene products through transcriptional, post-transcriptional, translational, and post-translational mechanisms. This, in turn, temporally coordinates many signaling pathways, metabolic activity, organelles' structure and functions, as well as the cell cycle and the tissue-specific functions of differentiated cells. When the functions of these circadian oscillators are disrupted by age, environment, or genetic mutation, the temporal coordination of cellular functions is lost, reducing organismal health and fitness.

Introduction

Life evolved with daily predictable changes in light, temperature, and food availability. With sunlight being the primary source of energy for photosynthetic organisms, there was a strong evolutionary pressure to produce carbohydrates during the day and store them for use during "nighttime fasting." This might have given rise to daily rhythms in metabolism, with anabolic and catabolic pathways operating at different times of the day. Such intense pressure for the temporal regulation of cellular processes in an ~24-h time scale is likely to have contributed to the evolution of circadian oscillators in diverse organisms, ranging from unicellular photosynthetic cyanobacteria to multicellular heterotrophic mammals.

A better understanding of the interactions between the circadian clock and cellular biology in physiological conditions is required to apprehend how their disturbance can lead to pathological development. Disruption of the clock has been associated with human cancers (Fu and Kettner, 2013; Haus and Smolensky, 2013), metabolic diseases (Dupuis et al., 2010; Paschos, 2015), and aging in mice (Libert et al., 2012; Chen et al., 2014; Fonseca Costa and Ripperger, 2015). Targeting the circadian clock could lead to new therapeutic approaches to treat these diseases. The focus of this review is to provide a broad overview of our current knowledge of the circadian biology of the cell, as defined by cellular activities that show diurnal oscillations that are controlled by the cell's circadian clock. Although we focus on circadian rhythms in mammalian cells, examples from other organisms are discussed to illustrate the variety of mechanisms used to generate circadian oscillations and demonstrate the universality of the control of cell biology by circadian clocks.

The molecular clockwork of circadian rhythms: Different mechanisms to create 24-h oscillations
Common properties of different clock systems

Circadian oscillators are self-sustained, with an ~24-h rhythm under constant conditions, yet possess plasticity to integrate intracellular and environmental changes to temporally regulate a diverse set of cellular functions and optimize adaptation (see text box). Entrainment by external cues (called zeitgebers) such as light, food, or temperature allow clock-controlled processes to be tuned to actual environmental conditions. Circadian oscillators are also temperature compensated, allowing them to function with ~24-h periodicity within a wide range of temperatures. Despite their common properties, clock mechanisms across the phylogenetic kingdoms use different modalities to generate ~24-h oscillations (Fig. 1).

Yet, let us stop for the moment and ask why the three patterned ensemble of "number learning/arithmetic/Mathematic's" are thought to be so important to make it a compulsory requirement from elementary school onward, and not just take it for granted that it is important. However, instead of reciting what some readers may think is an expected long list of obvious accreditations and supplementary supportive data, let me simply state because we have created a world in which knowledge of numbers, of arithmetic and even rudimentary Mathematic's is needed, everyone should have some knowledge and usage thereof.

Let us look at Mathematic's as if it were an infection:

Is Mathematic's a symbiont? For good or ill, is it a disease? Is it an unrecognized narcotic like some endorphin? Whereas we could otherwise label these as separate "zones" of activity, how do we describe Mathematic's origin and continuance if we use the analogy of some biological entity? Is it an invader which has taken up residence seeking certain individuals to speak on its behalf like some alien that has no other means of making its presence known? Is it a residual... though growing effect of some unrecognized pollutant?. And while the reader may be humored by such questions, it is an effort to view Mathematic's from a position which might assist us in developing a larger appreciation of its boundaries which can be expanded... or curtailed like pruning a tree or manicuring a lawn or planting the best trees for an orchard. Can we apply some measure of anthropomorphism to Mathematics whereby as a living being, we can better recognize its merits and failings so as to intentionally breed the next... better generation of Mathematics or recognize it as a barrier, a detour to a better, a higher level of cognitive expression? Whereas Mathematics consumes human energy like many living things which consume different forms of energy, let us ask if that energy is used up without leaving behind waste, or is the waste seen in the rountinization of certain equations be 'expelled' (expressed) by those just learning mathematics? Is there ever a point when Mathematics consumes energy and does not leave behind either a waste product or useful product?

If we take a general summation of human physiological processes and design parameters, we might well conclude that the human species is a collection of primitive species in each cell called organelles, and that due to the reality which we encounter multiple deformations, vestigial structures, and incongruities such as the placement of the ulnar nerve in a terrible place which creates repetitive motion injuries such as tennis elbow requiring surgery as well as repetitive motion injuries which are labeled Carpal tunnel syndrome; we can easily advance the proposition that the human body is far from being perfect. If humanity is in the image of its god, than that god is particularly primitive. And as a primitive god- species "in charge of" its earthly children... deciding at what time (period in history) that it should come to realize developmental pre-requisites of language, literature, art, music, collecting, geometry, collation, labeling, counting, enumeration, chemistry, philosophy, industry, politics, entrepreneurship, arithmetic, mathematics, agriculture, metallurgy, astronomy, physics, biology, geology, anthropology, archeology, architecture, dance, theater, sport, warfare, etc.; these supposed god-endowed physical expressibilities and mental/emotional functionalities can be viewed as add-on scripting to the underlying biological software that can have (under certain environmental pressures) an impact on changing physical components/"entities" (muscles, bone structure, immunities, etc.,) which can be viewed as acting in accord with "add-on" externalities which become incorporated in the human species just as organelles became compiled into a structure called a cell. The human body thus becomes the cell in which one or more of these externalities take up shop and exert a minor, mediocre or major influence... thus creating the condition of mutualized dependencies... but also specialized constraints and an increase inflexibility towards being receptive to any other externality that the god-species wishes to provide at a different time period after such initial add-ons have been around for awhile. Indeed, it is quite silly for humanity to consider that the present subjects humanity uses are the epitome of all add-ons that shall ever be made available to it.

No less, whereas one may easily recognize when a person reaches a supposed "higher" grasp of "higher" mathematics, how does the human species become aware of the presence of a new god-species endowed "add-on" that has the ability, after its initial debut in a rough, crude, other-wise immature and innocent (or insolent adolescent) form in the presence of so-called believed in higher "truths" and centuries-long practiced earlier add-ons? How are we to recognize a higher religious truth if all present forms of religion... being practiced for centuries... view themselves as "THE" most superior expression of all of the god-species endowments or "gifts"? How does one recognize a superior mathematics if everyone believes that present forms are "THE" utmost expressive form in which all truths MUST emerge or they are not to be considered viable? Likewise music. If we come to mathematically recognize certain repeating patterns and thus distinguish such patterns or such groups of numerical references as that from which all great music arises, what then does that say about flexibility and openness to a greater form as well as formula meant for the "taste" of a different mentality/emotionality of a more evolved species?

What if the next evolutionary stage of humanity rests on the ability of one or more humans to collate the available add-ons into a cellular form of thinking ... be it by way of analogy, metaphor or other tool of basic arithmetic additions, subtractions, multiplications, divisions, geometric inter-connections, algebraic continuities, and fractured (including fractions and fractals) to be found by using a dynamic form of Calculus, though it will eventually acquire its own labeling and be disunited from the word Calculus? When it is easy for some to see that the manipulations of numbers and symbols in math equations is a very simplistic visual exercise akin to a Rubric's cube's mix and match convolutions effected by physical affectations to complete a desired effectuation by completing a series of required moves within a given set of parameters; why is it that such a comprehension expressed in a different type of "add-on" is not convincing enough? Why must an ability to comprehend the simplicity of suggested and defined "higher" subject material only to be understood as a factuality if a person uses that type of add-on to exhibit competency of having acquired a different model of higher truth revel-ation? How are you to possibly grasp a higher truth occurring in a different model of expression if you feel/think the one you are most competent in is the most purest form of finding, knowing, and expressing that which you consider to be some ultimate truth... or a genuine path along which such a truth or truths can only be discovered... and thus are confident to pursue such a path with a determination like a bull charging after a supposed antagonist to declare itself victorious once one feels the perpetrator of the assumed assault has been vanquished in such a way to be interpreted as having been sufficiently subdued to a form over which one stands triumphantly and feels they are in command, in control of not only the outcome but how it should be interpreted and defined in accord with one's standards or the standards set forth by those who share in a similar mindset like so many cult members?

With respect to the words "fractal, fractions, fractured", though there are other terms which can be used to describe three generalized conditions:

• Distinct (known... applied or not) [A grammatical period.]
• Semi-distinct (theorized, supposed, hypothesized) [A grammatical question mark.]
• Indistinct (unknown, unrealized, unrecognized, not thought about) [A grammatical exclamation point... signifying a absolute view of non-existence, or that which may exist but not in the human reality.]

---

Date of Origination: 26 February 2021... 6:59 AM
Initial Posting: June 4th, 2021...3:48 AM