(Static -vrs- Dynamic)
9a
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021


Numbers and Mathematical activity is pervasive amongst the human species, whether or not everyone is consciously aware of such an occurrence frequently, inter-mittantly or only when they are subjected to a context where mathematics is being discussed, such as a classroom. Such is the case for mathematical thinking. While most people appear to develop only a basic sense of number, this does not automatically describe the same people as never engaging in more complex mathematical types of thought activity, even though they may never use the (modern) language of mathematics in any conventional sense. If the many "complexifications" of thought could be viewed in terms of mathematical equations, it might well be noted that there exist mathematical geniuses who are otherwise viewed as a housewife, gardener, seamstress, tennis player, chef, mechanic, plumber, electrician, janitor, photographer, artist, etc.. or even as a person who is viewed as a "ne'er-do-well" [never-do-well] sometimes referred to as lazy, irresponsible, idle, worthless, rascal [rapscallion], couch potato, bum, shiftless, scalawag/scallywag, low-life, dreamer, beatnik, (Beat Movement), hippie, drifter, delinquent (now called Bad Boy/Girl), intractable, peasant, degenerate, slot, counter-culture, anti-establishmentors, good-for-nothing, artist, poet, writer, vagabond, hobo, tenement dweller, party girl/boy, hipster, etc...).
Everyone apparently thinks in mathematical terms in some sense. Whether it be on a basic counting level or something more complex, requiring more memorization such as playing chess, engaged in choosing lottery numbers, betting on horses, playing cards, shooting billiards/pool, calculating a check book (even though check books are not customarily used as much as they used to be), or calculating what and how much food needs to be prepared where and when for a large family whose inhabitants comprise multiple age groups with diverse interests requiring different life-style scheduling. If everyone in the world could be trained to focus all their mental activity towards mathematical expressions, the world would be a different place with a different social mill eau and aura of interaction. Yet, this says noting about those instances of mental activity where insights, illuminations and inventiveness embark upon human consciousness and act as a mile-marker demarcating a point of departure into a new realm of realization.
Such points of demarcation do and have arisen in all human activity and sometimes lead to the development of an institution of thought and activity that become run by those who do not wish to have their positions nor ideas threatened by a different way of thinking. This is true in Business, Religions, Politics, Sports, Art, Music, Science, etc... Many different forms and formulas of elaboration are configured and put into practice that will keep the majority of people burdened by expectations that they 'toe-the-line' and not upset the apple cart nor stand up in a small boat... at least these are the conjecture warnings of some, just as is the case when a religion uses its multiple models of right and wrong to present itself as knowing all the answers, as if it is a representative model of a supposed all seeing, all knowing, all present god. Most facets of society do not want people to be progressive beyond that which is controlled by others. You are brought up to conform. Yet, many of us cannot. We therefore maintain a sustained interest and effort to express our way of thinking and develop proof as to the existence of a different orientation that we believe is meant to be a step beyond the convention line of thinking... or at least the line of thinking that we consider to be a standard convention... though in this respect, many people misinterpret what they perceive to be a convention only because it is developed from the vantage point of a very low step within the context of their particular environment. Whereas they may think to themselves that they are standing on the shoulders of giants enabling them to see further— as a statement attributed to Sir Isaac Newton, they do not recognize that their respective giants are sitting down in the bottom of a canyon next to a bottomless precipice.
However, this in no way is meant to disparage any effort with an attempted expression indicating a step beyond convention towards a new horizon of appreciation. While some efforts at expression are primitively rudimentary and others sketched or doodled outlines providing one or more examples of a "work in progress" development, others are a bit more illustrative, even though the language being used in the description is not the exact accent nor spoken of in a contextual dialogue typically articulated in the manner of expectation for a given subject area. For example, when initial efforts by early mathematicians were directed towards applying their craft to non-mathematical areas of research, no doubt they received raised eyebrow looks of disbelief and resistance from those who believe that mathematics can not hope to adequately nor accurately understand nor express someone's domain where a different type of language is used. For example, this article: Logic is not Math assets that logic and math are different animals, so to speak. Thus we have an instance where a different type of human thinking is said to be a different species of thought processing and not viewed as either a parent nor sibling or other relation to mathematics. Hmmm, a world where mathematics does not exist, until of course we start to count some aspect thereof and relate a particular idea of this claimed non-mathematical entity to a mathematical construct. Granted that if one searches for a given numerical or mathematical existence in an otherwise viewed non-mathematical state of being we can find such, one should not automatically suggest that this means the entity is a mathematical creature as well. If we view mathematics as a sponge then of course it may well absorb all subject areas. But if we view it as a tool that must be fashioned to fit the nuts and bolts, screws and nail of a given subject, then we must accept that while mathematics is readily flexible and adaptable to a multitude of different entities, those entities need not themselves be interpreted as being basically mathematical themselves. We can give all subjects the benefit of a doubt for believing themselves to be separate and special entities in their own right and not as a poorly developed form of mathematics.
If we view mathematics as some sort of underlying genetic code for all entities of human conceptualization, and those entities are merely different species having developed their specificities of expression due to the constraints of the environments from which they emerged, then we must ask what, if anything, is at the bottom of mathematics? Could it not also be a "wild" flower having developed under different circumstances that is now bred with different breeds of mathematics in mind and afterwards designated a standard form... albeit a standard form having arisen due to the artificialization of domestication? And since we are using the analogy of biology in this context, can we not also include the possibility that at new form of life might well arise... though some may interpret it to be the arrival not of a new species but of a species that was thought lost? Hence, such that when counting was figured to be the standard form of mathematics in the distant past, only to be usurped in its dominant position by geometry and then again by Algebra and later forms of mathematics; it should be of no surprise to find the development of a new idea from which a further development of mathematics is to be sighted.
While Calculus deals with variations of limits and infinitesimals, which appear to provide us with tools to cover every aspect of perceived reality from a given vantage point, it should be understood that calculus arose as a later addition to human conceptualization as a rigorous discipline. However, bits and pieces of it existed and was practices elsewhere as described on the pages of these three examples:
- Wikipedia: Calculus
- What is Calculus? When do you use in the real world?t by teÅchnology
- What is Calculus? Definitions and Practical Application" By Deb Russell, January 21, 2020
The last selection pin points... or at least provides the direction I want to address, concerning static mathematics. While the author provides the following comment asserting that Calculus deals with dynamical properties and therefore suggests that Calculus is dynamic as well; from my viewpoint her comment needs to be flipped around.
"Calculus is a branch of mathematics that involves the study of rates of change. Before calculus was invented, all math was static: It could only help calculate objects that were perfectly still. But the universe is constantly moving and changing. No objects—from the stars in space to subatomic particles or cells in the body—are always at rest. Indeed, just about everything in the universe is constantly moving. Calculus helped to determine how particles, stars, and matter actually move and change in real time."
The problem with the author's statement is that:
Although Calculus deals with dynamical properties such as movement,
(Calculus) itself is not in motion.
Calculus is not reminiscent of an actual analog clock which displays visibly moving hands or a digital device exhibiting incrementally changing numbers. A Calculus equation is not the sum of individual parts that emerge as an entity in motion. The elements are more like stepping stones or knots on a rope or beads on an Abacus which allows us to mentally move from one position of thought to the next like a dot-to-dot or paint-by-numbers tool. It helps to organize thoughts in a given fashion and mark those positions like a child playing hopscotch. It is like a tally sheet and therefore might be viewed as an elaborate model of an accounting ledger. The equation does not move even though someone might animate an equation for teaching purposes. All equations are static. While static equations can increase the way in which our thoughts move, just as a piece of artwork, architecture, sheet of music, etc..., it is we humans which use such mediums to control our thoughts and emotions and physical activity. Like exercise routines that we may follow to the letter, or improvise additions and subtractions, multiplications and divisions of the rules we have set forth. Equations very often act as constraints, tether-lines, and even life-lines as we attempt to ascend, descend and overall investigate what we may chance upon to explore and investigate. It is unusual for a mathematician to simply free-fall thought processes during some moment of spelunking those hitherto unexplored regions of consideration found in different subjects. The elements of equations can act as bread crumbs, as notches, as broken twigs, or some other tell-tale sign of which way we came in case we encounter a moment in our explorations where we begin to feel we are lost or ran into some impasse... if not some repetition which gives the impression of fruitlessness (or "more of the same") if we continue further in the same fashion. Static equations are like a standard tool box containing the typical assortment of screwdrivers, wrenches, pliers and hammers. While some equations are speciality tools, they too become adopted as standardizations which may inhibit a person designing a better tool so long as they are set in their ways and are possessed by the inclination of rationalizing the importance of those tools which were acquired by great effort and financial cost.
For example, many decades ago I worked with a young man who had paid to go to a diesel mechanic's training school and invested an enormous amount of money purchasing a complete set of tools (along with tool boxes) from Snap On. Others did the same thing except they purchased a complete set of tools from a competing tool company such as Mac tools, while other (older) mechanics picked up whatever tool would get the job done without having to pay an arm and a leg for such name-brand tools. Having a collection of name brand tools helped the younger mechanics be overlooked for their inexperience, while all the time providing for themselves the perceptual feature of being a good mechanic because sales pitches stating that all good mechanics use one or another brand of tools is an idea that some mechanics buy into as representative of themselves... just as many a title or name badge does for others. Because so much of their ego was vested in their tools and tool boxes, an employer need only realize they simply had to invest in the person's ego and get them to work at a cheaper rate. While I had not worked on many diesels in that era but had experience working on gasoline powered vehicles, my knowledge of rebuilding and tuning was years ahead of these young guys (who were actually older than me).
On one occasion I had to encourage a mechanic to perform a valve adjustment on a diesel engine because he had never done one and remarked that he would have to use a book. If you don't know the valve lash of a particular vehicle it is a necessity to look at a manual. To me, adjusting valve lashes was a typical routine job... particularly when in those days the engine compartment was not cluttered nor the engine shoe-horned into place. I wouldn't want to attempt this as a routine on today's vehicles, much less switch out camshafts, cylinder heads, pistons and the like. In any respect, we find that the equations being used by some mathematicians is more due to a highly invested ego application that they are in possession of... and use as a mirror image of some supposed personal uniqueness, while other mathematicians sometimes engage in the usage of a tool called intuition that they neither try to expose as some unique quality of themselves nor patent for the purpose of resell. Even though intuition can be a hit and miss type of adjustable wrench, it is something that finds usefulness on occasion and may impress onlookers, though a person's inability to use it for everything quickly humbles them unless they deliberately attempt to create or remain in an environment where such a tool advantages them over another.
Calculus retains manifest and vestigial remnants of its originating past which embodies static linear equations aligned with rudimentary orientations as do all present current practices of so-called modernized subject material. Simply put, Mathematics is like a current organized religion with its many precepts, rituals, observances, literature and practices which have come to conceal their ancient ideologies with embellishments which attempt to give the impression that its partitioners are enlightened and have no need of ancient perspectives labeled as paganism. Take for example the different usage of a triad such as the Christian Trinity or Hindu Trimurti, both of which have an ancient origin in solar worship... where the three entities are embellishments of the Sun's three distinct "moments" labeled as Dawn- Noon- Dusk. At present, we might even conjecture that this set-of-three during the early years of biological precursor development (when the Earth was spinning faster and there was a different level of ozone), influenced the development of multiple other "threes" such as the triplet code of DNA, the three macromolecules (RNA- DNA- Proteins), etc., unless we want to claim that the three sub-atomic particles known as Protons- Neutrons- Electrons left a three-patterned mark or brand on many items which followed.
Mathematics is the accumulation of "pagan" ideas which have been linguistically contoured to give the impression its partitioners have been endowed with greater revelations making them into latter-day Saints of the subject matter. It is of interest to note how the development of mathematics provides a similitude of expressed development found in other subjects such as Religion, Commerce, Science, Education, and government. Like all "later born" (teenage and young adult centuries... 13th, 14th, 15th, etc...) religions which have adopted philosophies consistent with mentalities with larger embodiments of knowledge, experience and day-to-day information from multiple sources that are used to manufacture an enlarged stock of rationalizations to deal with the many competing ideologies, the language, dress code, social behavior and multiple other personalized behavioral characterizations come to reflect characterizations which make mathematics appear as normal, natural and especially viable because of its supposed many talents... like a person whose skills and training make them particularly amenable and useful for the changing conditions of economics which can be fickle, idiosyncratic, socio-pathic, neurotic, psychotic, schizophrenic, bipolar, as well as exhibit one or another addictions, mal-developments, or whatever is required to get sympathy and arrange for itself a government sponsored dependency. Dissecting the cognitive roots of Mathematics is of especial importance if we wish to develop it further by revealing that which is holding its development back, such as investigation its current usage of (quantifiable) ancient superstitions which continue to linger by being cloaked in the accepted garments ("hiding in plain sight" forms of camouflage) of today's many environments it has taken up residence in. Mathematics must come to be noted for the race, gender and species that it is, and how it has migrated into the cultures of different subjects (like a symbiotic organism) and assumed the adoption of practicing the adage of... "While in Rome, do as the Romans do". The different subjects to which mathematics has ingratiated itself must turn their individualized respective tools of dissection on (and if necessary, against) mathematics. For example, we can view Mathematics Anthropologically, Archaeologically, Sociologically, Biologically, Criminologically, Demographically, Geologically, Paleontologically, Politically, Chronologically, Comparatively, Statistically, Numismatically, "Gaministicallly" (Game theory), Philosophically, Linguistically, etc...
For example, someone might come to identify that one or more contours of mathematics resembles a cognitive gymnastics game with repeating routines which prevent it from achieving a greater goal of personalized accomplishment in a given field of application.... Like a person stuck on using a given exercise routine and dietary regime which are counter-productive to a goal of becoming an Olympic athlete.
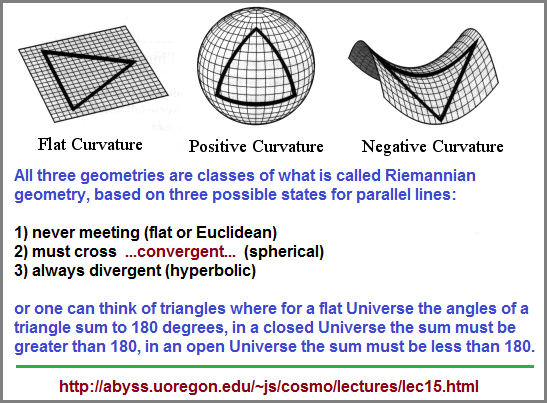
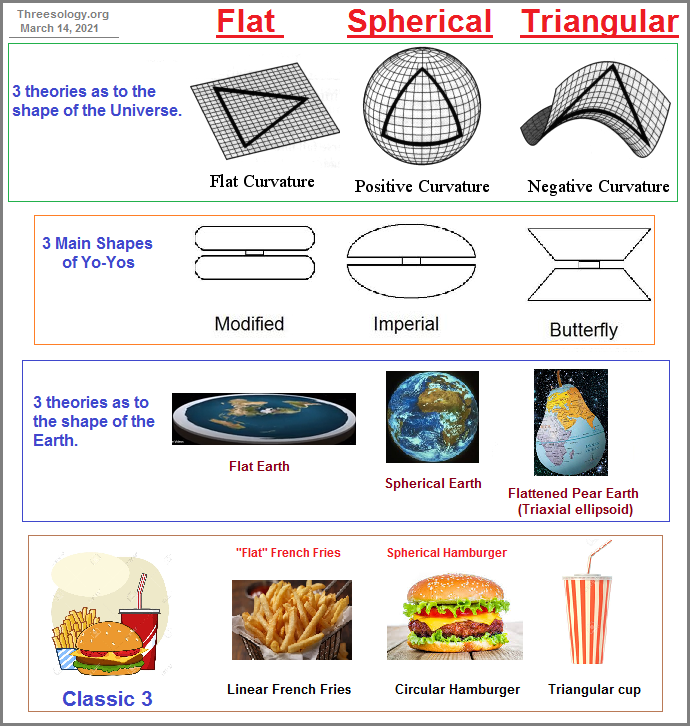
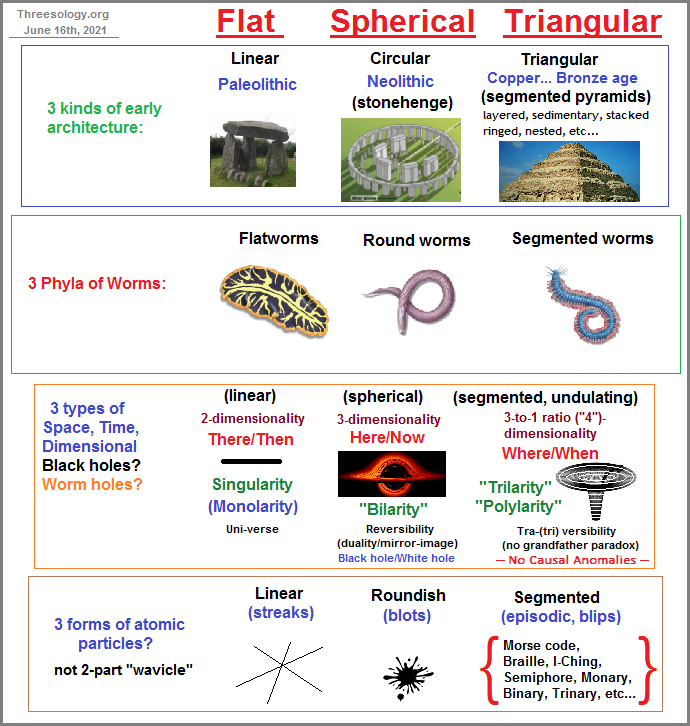
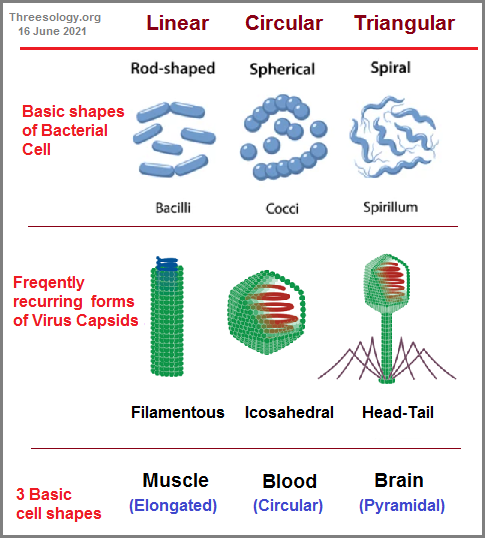
If we assume that the "arrow" of time is in motion because we view time both as being linear and in constant motion, how do we describe such a dynamical property if the arrow's beginning and end are infinite and we can only image what such points represent? While an arrow can suggest movement, it can also (only) represent direction from a given place and time according to observation. Is time Linear? Flat? Circular? Segmented? Unilateral? Bilateral? Trilateral? Multi-lateral?Is it a predatory entity? Is it a herbivore? Is it an omnivore? Does it exist multi-dimensionally? Does it or can it be splintered? Can a so-called "grandfather paradox" be circumvented by time branching into different time-zone results, whereby one can go back in time to kill one's grandfather which will affect one timeline but not another or others? Similarly, are there three types of Black holes corresponding to worm holes which correspond to the three biological categorizations of worms... namely, flat worms, round worms, segmented worms? Do not these reflect the three types of "body plans" physicists have imagined for the shape of the Universe... namely, Flat, Spherical, and Saddle-shaped (triangularly-segmented)? (In two dimensions there are 3 geometries: Euclidean, spherical, and hyperbolic: The Three Geometries.)
Is there a value between the ideas of an infinite and finite Universe that is exceptionally different which does not admit to some add, subtract, multiply or divide value? Is there a distinct third entity which is not negative, positive nor zero? Let me provide a few correlations of the Flat (linear), Spherical (circular), and Triangular (saddle-shaped) geometries which bring to mind the three bones of the Ear (Incus- Malleus- Stapes, or anvil, hammer, and stirrup. The stirrup can be aligned with the saddle, the hammer with a bulbous (round) sphere and the anvil as a widened linear object. If you disconnect the attachment ends of the three auditory ossicles the Linear- Circular- Triangular configurations are more easily noted. The usage of the words "hammer" and "anvil" detract from making an easier correlation with basic circular and linear geometries.

While investigating the geometrical phenomena of linear, circular and triangular configurations, some questions come to mind:
- Whether the 3 terms (linear, circular, triangular) are crude approximations of some other unnamed structure providing clearer research advantages.
- Where (at what point) we should begin to define an object or instance or perception as being linear, or circular or triangular.
- Does the word "linear" describe particular dimensions such as width and length... or can a line be intermittent dashes, dots, spaces, sounds, etc...?
- Does the word "circular" exclude circular-like objects such as octagons or circular possible objects such as squares?
- Does the word "trangular" only mean equal sides such as an equalateral triangle, or can other triangular-like shapes be included such as a multi-triangle star or two-line configurations which do not count the surface or bottom as a line such as an inverted V-shape?
When we read the following excerpt, it reads like a weather report of high, low and "even" pressures, except that we are dealing with mass, energy and gravity... if not time, speed, vacuum, volume, etc.,— as variables. If we incorporate the idea of an encircling (rotating) tornado (cyclone) as a spiraling blackhole, then creating a blackhole for some supposed short-cut interstellar travel might be created by an artificially induced gravitational sphere by way of an alternating (or Direct Current) magnetic field (or intermittent combination) where polarizations can be variably minimized and maximized for processing the central calm (core) meteorologically referred to as the "eye-of-storm"... and yet, why circular shapes?... (Circular motions of "funnel/triangular-shaped" expressions exhibiting linear paths.)

"There are basically three possible shapes to the Universe; a flat Universe (Euclidean or zero curvature), a spherical or closed Universe (positive curvature) or a hyperbolic or open Universe (negative curvature). Note that this curvature is similar to space-time curvature due to stellar masses except that the entire mass of the Universe determines the curvature. So a high mass/high energy Universe has positive curvature, a low mass/low energy Universe has negative curvature." (Geometry of the Universe)
It is a fallacy to think of Calculus being in motion. It is a static tool using linear equations that are attached to movement like one or more rubber bands placed around a ball and then claim the rubber band is full of motion... unless one thinks of the rubber band as a collection of moving atomic particles. Alternatively, one might use the analogy that Calculus is like a person involved in the observation of a clock's moving hands; yet the observer remains static... or at least exists in a conserved state of observation; despite the degradations of cellular process of the observer's physiology which can be claimed to be in motion. Linear equations are customarily used to describe dynamical properties, like a hominid whose mindset configures perceptions within the constraints of their personal experiences according to the prevailing intellectual environment they inhabit. Most Mathematicians are like prehistoric hominids that have gravitated towards a shoreline as a means of establishing some measure of survivable equilibrium. Whereas some (intellectually/visually) move further inland and thus begin to adopt the intellectual/visual survival skills for the terrain they find themselves in, most of them continue to use some variation of linear equations as their preferred tool. However, some do begin to adopt rudimentary tools resembling more robust (circular) configurations of thought, and a rare few journey further inland and upward towards higher intellectual/visual landscapes of consideration; the different types of visualization/intellectualization do not come to pay witness to the difference in orientations related to intellectual/visual altitudes which represent linear, circular, triangular configurations crudely suggested by the different types of trees we see at different elevations:
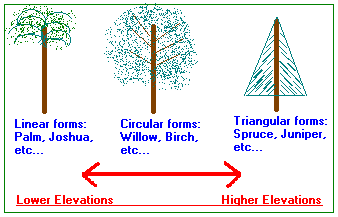
If we try to make a correlation of these three general ideological/body plans with those seen in animal structures and note the commonly delineated forms as Asymmetrical, Bilateral, and Radial; a 1 to 1 corresponding alignment problem may arise for some because they may consider that the bilateral form (such as that seen in humans suggests a linear expression when viewed an upright standing human form. Whereas the Radial body plan suggest circularity, the Asymmetrical body plan does not at first appear to suggest either a linear, circular, or triangular model. With respect to humans, the fact that its anatomy can be listed as series of Threes in human anatomy does not appear to suggest to some that they are viewing a triangulate species... at least anatomically speaking, and even though multiple ideas are arranged in patterns-of-three.
A simplification of the three body plans related to the three germ layer development is seen in the differences between three "worm varieties: Worms: Phyla Platyhelmintes, Nematoda, and Annelida. (Annelida is further divided into three subclasses: Oligochaeta, Hirudinea and Polychaeta. The three Phyla of worms: flatworms, roundworms, and segmented worms.)
- Flatworms (phylum Platyhelminthes) are simple animals that are slightly more complex than a cnidarian.
- Roundworms (phylum Nematoda) have a slightly more complex body plan.
- Segmented worms (phylum Annelida) are the most complex animals with worm-like body plans.


On a more (aforementioned) basic body plan involving Asymmetrical, Radial and Bilateral animals with an intent of displaying a rudimentary association to linear, circular and triangular configurations (as a means of conveying the suggestion that the human brain/mind exhibits a quantifiable "body" plan expressed in its usage of mathematical forms of equations as well as a lack there of):
If we care to elaborate on the evolutionary development of the body plan and see it as a representative model of human thinking (viewed as a developing body plan). While the following is a "five" example from Five key transitions in the evolution of the animal body plan, this link says there are six: The Living World (The evolution of animals is marked by six key transitions: the evolution of tissues, bilateral symmetry, a body cavity, segmentation, molting, and deuterostome development.)
There have been five key transitions that have occurred in the evolution of the animal body plan. |
|
1. Evolution of tissues
|
|
2. Evolution of symmetry
|
|
3. Evolution of a body cavity Presence of a space within the body allows for more development of internal organs to perform specific functions, such as digestion, transport, and reproduction
|
|
4. Evolution of protostome and deuterostome development
|

|
|
5. Evolution of segmentation Segments or repeating parts of the body may provide 2 advantages
|
In cellular development that we may define as animation or dynamical, we see the usage of a doubling effect that might alternatively be described as a mirror-image bilateralism, where mathematics and geometry come into play, but current intellectual models are obstacles towards integrating the basic patterns with patterns found in other subjects which use languages and symbolism which inhibit a broader application and larger interpretation of more diverse investigations into multiple phenomena.

Date of Origination: 26 February 2021... 6:59 AM
Initial Posting: June 18th, 2021... 8:40 AM