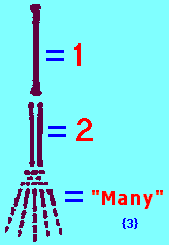page a
(The Study of Threes)
http://threesology.org
The three-patterned reference of One ~ Two ~ Many crops up in a variety of ways and circumstances to the extent of warranting an examination as a representation of an underlying mental pattern, that others might prefer to label as a fundamental cognitive construct. If we examine the literature of those who have attempted to reconstruct the History of Numbers, one of the recurring patterns that is encountered is a reference to the development of three number words by primitive people to identify and enumerate a concept of quantity relative to their uses in their particular social settings.
In the development of number usage for such things as counting crops, livestock, family members, gods, demons, cooking utensils, game animals, stars, mountain ranges, distances, etc., early peoples developing word-related numerical concepts centered for a time around the three number words:
- ONE for the quantity 1
- TWO for the quantity 2
- MANY for any quantity beyond 2
Hence, there were three number words.
Such a method of counting may very well have been coincident with the counting of one's fingers. The thumb was not counted and the little finger signified completion of the 3-finger count. Why the thumb and little digits were excluded in the 3-finger count is unknown to me, though we could venture to guess a variety of reasons involving superstition, identification with some animal's footprints, it's alternate position on the hand, etc., and the reason that the little finger was not likewise counted with the group was due to its small size. In other words, the thumb and little finger are the "odd man out."
Some readers may want to argue that there were other less-than-three number word usage periods, and that there was also a stoppage at the number four as a counting limit amongst some primitive peoples. While this is true, according to the literature, such readers do not see these references as part of the same 1~ 2~ 3 developmental structure, and they frequently overlook that with the usage of the number three as a distinct and separate quantity, that the value of zero was not considered as a number, whereby the reference of 0,1,2,3, is still a three-patterned reference of the three numbers 1,2,3, because "0" was not a number. In other words, its dismissal as an irrelevant item meant that primitive peoples maintained a three-patterned mental focus. And even when larger numerical concepts were beginning to be developed, what we find is that there is an exercise in repeating the usage of the three number quantities such as 1 + 1 + 1 or 1 + 2 + 3 or 3 + 3 + 3, etc., which is also evident in the repetitive usage of basic number words, symbols, number symbols, lines, X-es, circles, etc., such as is expressed in the present-day usage of counting by making a line and grouping the lines in fives:
The point to make is that we can not only find a recurring usage of a three-patterned mental formula, but we can also find a recurring usage of a reference to such a pattern, and also a reference to the reference of the three-patterned structure. Hence, this also is a pattern -of- three formula:
- Initial pattern-of-three.
- Reference to the initial pattern-of-three.
- Reference to the reference of the initial pattern-of-three.
Thus, there is the recurrence of a three-patterned mental construct.
Instead of labels One ~ Two ~ Many, we may find a usage of:
- 1 = mono..., uni..., single, primary, once, first, etc...
- 2 = bi..., di..., dual, duo, twice, secondary, second, etc...
- 3 = tri..., many, few, some, much, several, tertiary, thrice, plurality, etc...
While some readers may want to argue that words such as many, few, several, etc., may actually represent a distinct quantity of more than three items, or merely an arbitrary quantity beyond three, the point to make is that within the context of a three-patterned model of reference, the labels which denote the three-patterned structure can take on a variety of expressions depending on the context and structure of the items. Take for example the three eating utensils of Knife- Fork- Spoon. The Knife's appearance gives a symbolic representation of the number one, the word "Fork," suggests a two-pronged formulation such as is expressed in the idea of a forked-road, and the structure of the Spoon, to hold much or many, is clearly aligned to the 3rd placement in the context of three items.
As a momentary digression into the usage of words with an underlying expression towards an increased quantitative development, let me cite an example that some readers may find just as easily identifiable and understood once it is pointed out:
It may be of interest for some to note that the expression "and so on and so forth" can be imaginatively viewed as a mathematical sequence using words— that is if some measured liberality of interpretation is accepted as an aside reference to that which indicates a progression. But if you are one whose mind is constrained by some political, religious, business or academic intellectual restraint of convention, many of the presented ideas might well appear as an anomalous character which do not conform to predisposed idealisms. It is far better to walk in the present terrain as might a cultural anthropologist who is more committed to observation and recording, instead of judgemental interpretations which might presume some authoritative right to perpetrate disparagements because of some undisclosed personal insecurity. With such a disclaimer in mind as a proviso, let me continue with the following example:
Historically, with the development of using words to express numerical quantity which had periodic stopping points in the construction of concepts; it has been cited that primitive peoples used three number words consisting of, in their own language equivalent way, specific words for the quantities one and two,— but any quantity involving the value of three or more was considered "Many". While there were three number words (one, two, many), there was a cognitive limit of description for individual quantities above two until, we might assume, there was either a shift in cognitive perception and/or some physical brain change that we might further describe as being a developmental maturation... however this is a presumption based on the urban-legend-like notion that humanity is on a trek towards some "greater" human form with an equal increase in ideas, social constructions, etc...
Hence, after the quantity "two", was the notion of "and so on", expressed with a singular term such as "Many", though, conversationally speaking, the word "Much" might be included for consideration as an acceptable alternative. Thus, the expression and so on and so forth" might be viewed as an exploratory development of a concept after "three", called "forth" (i.e. "fourth"). While some readers may wince at the proposal of describing an assumed numerical reference with a similarity of spelling, it is of need to support the idea by citing that our present usage of the suffix "teen" as in thirteen, fourteen, fifteen, etc., was originally described as "three and ten", "four and ten", "five and ten", etc... The present usage of the 'word' "teen", represents the value of "ten", though the earlier meaning and method of reference have been set aside as a footnoted explication of how old ideas can be refashioned into the wardrobe of conception for a given era.
Since it is sometimes considered that "higher" concepts are developed in a sequential order, in that they are only developed after and not before or in conjunction with a "lower", "prior", "earlier" or "primitive" concept, the usage of a concept such as "forth" in reference to a quantity "four", is evidence for a false type of logic. Simply put, the usage of the word "forth" as a description for a "four" quantity is wrong because a word for the quantity "three" has not yet been established. Advances in conceptualization do not necessarily have to proceed along a simple sequential formula. Leaps of imagination, of intelligence, of faith, etc., can occur as do characteristics called mutation; to produce features which may in fact be an enhancement, but are not necessarily recognized as such until particular circumstances show the development as a desirable feature. The reason for introducing such a consideration is to compare it with the usage of the word "Cenocracy" (New Government) to "Democracy" (Peoples Rule/ Peoples Governing-rule/Peoples Government) as a beginning point of departure into a "higher" realm of a social self-governing perspective by illustrating it as "Cenodemocracy" (New Peoples Government-rule). Indeed, we of the present are a new people in need of a new concept to further the beginning of a new Age desirous of a full expression being oppressed by the present form of Democracy.
With respect to the 1- 2- Many counting sequence of early humans, we can see a repeat of this three-word distinction when we reach the counting limit of ten:
11 (eleven)- 12 (twelve)- 13,14,15,16,17,18,19 ("Many" teens)...
Additionally, another example is found in the concept of the 3 common clothing sizes which are typically represented with the words Small ~ Medium ~ Large, but are not typically referenced with the numerical values of 1 ~ 2 ~ 3. Nonetheless, the verbal arrangement of these three sizes can be attributed with the three numbers. While some may feel this to be a stretch of the imagination, the three sizes after the standard large reference, are clearly representative of the 3 numerical values since they are displayed with 1, 2, and 3 X's: X- large, XX- large, XXX-large. No less, with respect to the idea of number concept limit, the 3rd item of the first set of three, which is "large," is repeated for those sizes which are meant to illustrate a different unit.
...In other words, just as when primitive peoples reached the third position in their number concept formulation as a cognitive limitation, so has modern people with their usage of sizes beyond the concept of large. Instead of developing a separate value for larger sizes which don't use the word "large" in a repetitive manner as did primitive peoples in their counting systems, we are simply expressing the same three-patterned cognitive limitation... in other words we of the present are using a modern-day form of cutting notches on a stick, inscribing lines on a stone or ground, etc...
Is this the result of a limitation that is inherent in the symbols we refer to as numbers, or is this an indication of an underlying pattern of human mental development that is repeating itself due to:
A defect in mental development brought on by poor nutrition, genetics, environmental conditions?
Number symbol construction? (Are our number symbols equivalent to the limitations imposed upon mathematicians attempting to use pictures as the ancient Egyptians did?)
Limitation of the present Human species, whereby more advanced mathematics will only be possible with the birth of a new species that is better equipped?
Here is another perspective of the One ~ Two ~ Many formula:
One, Two and Many: The Movement of Philosophy
A perennial question of philosophy has concerned itself with the number of realities rather than the nature of reality. Three general answers have been theorized centering around the numerical ideas of one, two and many.
The idea of one reality finds expression in the philosophy of monism and the belief reality is one impenetrable unity. It emphasizes the sameness of the world rather than its separateness and diversity. The idea of two realities is expressed in the philosophy of dualism and its belief in two realities. While a number of possibilities have been suggested for these two realities most have centered around the duality between material and spiritual reality and the division of the world into objective and subjective realities. The idea of many realities finds expression in the philosophy of pluralism and the belief in many realities.
Pluralism emphasizes:
- Diversity rather than homogeneity.
- Multiplicity rather than unity.
- Difference rather than sameness.
It is useful to view these three philosophical distinctions ("questions") as essentially symbolic ones. The traditional definition of a symbol is something that refers to something else. One needs to extend this definition though and say that a symbol is something created by culture that refers to something outside of culture. The only something outside of culture is nature. Therefore, one can say that philosophy is a creation of culture which produces a system of symbols referring to nature.
--- Symbolism Org.- One, Two, Many ---
http://www.symbolism.org/writing/articles/internal/one-two/home.html
The problem with the above view is that many philosophers tend to stay within the confines of philosophy proper and do not venture too far afield in search for examples that illustrate the reference to nature. While some of them may be thinking to themselves about examples in nature that give reference to the One ~ Two ~ Many, they won't express this in their writings nor public conversations. They may discuss the One ~ Two ~ Many as a triadic formula, and suggest it is like other triadic constructs, from which they may or may not then develop their own triadic formula, they do not provide a large sampling of triadic formulations from different interests, and prefer to rely upon the triadic views of others who came before them, and who have also remained primarily within the parameters of philosophy. Many of them are wholly unaware that such may be a process of the same limitation of cognitive structuring whereby their own analysis becomes like someone merely adding a notch to a series of other notches on a stick that will come to decompose as a natural process of decay.
This image is an example of a 1 - 2 - Many characteristic that is commonly overlooked because it is customarily referred to as an item representing the numerical designation of "five" by being described as a pentadactyl (five finger/toe)- structure. However, interestingly enough, the "dactyl" portion is said to be analogous with the three joints of a finger.
............entry: 06-17-2011, Friday, 4:57 AM Numerically the arrangement reads (with respect to the number of bones portrayed in the image): 1-2-5-2-5-20, or alphabetically it reads: A-B-E-B-E-T. Perhaps if we were to assign letters to all the number of respective bone arrangements a larger "statement" could be read.............
And from a dictionary we encounter:
A metrical foot consisting, in Greek and Latin verse, of one long syllable followed by two short ones, or, as in English verses, of one accented syllable followed by two unaccented ones.
Here is another example of a one - two - many expression found in a discussion of the Trinity and the Tripartite Indo-European world-view. You many not get any hint of a numerical reference until the third word in the series is defined:
...Much more familiar is a passage in the Old Testament, the Shema:
Hear, O Israel: The LORD our God is one LORD; and you shall love the LORD your God with all your heart [levav], with all your soul [nephesh], and with all your might [meod]. (Deuteronomy 6.4-5, RSV)
Hear, O Israel: The LORD is our God, the LORD alone; and you shall love the LORD your God with all your heart [levav], with all your soul [nephesh], and with all your might [meod]. (Deuteronomy 6.4-5, NewRSV, also Tanakh)
Both the RSV and the NRSV, as well as Tanakh, the New JPS translation, translate levav, nephesh, and meod as heart, soul, and might, not yet exactly an IE (Dumezilian) triad, but a translation which follows the Septuagint, which has kardia, psuche, and dunamis. The Gospels quote the passage, but they have changed it. Kardia remains, but psuche has been supplemented by dianoia (mind). In Mark and Luke, dunamis has become ischus, which also means "strength." In Matthew it has been deleted. The result is to force the Shema toward IE (Indo-European) categories, whereby the first and second functions are displayed unambiguously. The original sense of the series levav - nephesh - meod might have been preserved in translation, but as we have it, it was not. Meod has been treated the worst in the NT translation; lost in Matthew, it appears as "strength" in Mark and Luke, but strength is not really its central meaning. Examination of the usage of these words in the Common Documents translated as Old Testament and of the comments in a lexicon amply confirms the suspicion that in translation they are often forced to become IE function-specific.
Translations into one or another IE language may differ, but the closest example (English) will exhibit the problems of translation well enough. The Brown-Driver-Briggs lexicon and concordances illustrate the function-neutrality of these words.
Lev, the root of levav, the first term in the series in the Shema, would seem to defy its translations, for it is translated in so many ways. Although in the overwhelming majority of cases it appears as "heart," it also is translated as "mind," "understanding," "wisdom," and significantly, "midst," and even once, "consent." It is the inside as opposed to the externals, occasionally even of things (the midst of the sea). It is seat of will and emotions: passions, appetites, trouble, courage, sorrow and joy, not just the intellectual faculties. And it is the seat of moral character. Clearly, it cannot be assigned to any one of the three IE functions, and the translation as "heart" is accordingly a reasonable one.
Nephesh, the second in the series, is usually translated as "soul," and Brown-Driver-Briggs even remark that it is often assimilated to lev. But its other meanings are instructive, for its second meaning is "life," and by extension, "body," "person," "beast," "man," "mind," "will," "desire," "self." It verges on being a substitute for pronouns -- the essential of a person stands for the person himself. If lev is the inner man, nephesh is the inner part that stands for the whole. Like lev, nephesh does not fit into an IE function, and "soul" preserves this neutrality, but the richness of its less frequent translations could easily be forgotten in its most common translation.
Meod is the most surprising of the three. It appears as "strength" or "might" in the translations of the Shema, and this might seem to fit into the IE second function. But far more common is its use as an adverb: "exceedingly," "greatly," and related ideas; the most frequent translation of all, out-numbering all others, is simply "very". The root can mean "to add," hence what one gets after addition -- more, muchness. Some translations show it as "money" or "property";(44) so it manifests neutral and possibly third function meanings, but not really a second function meaning of force, contrary to what appears in the translations. Even a meaning of "money" or "property" is more as an example of its sense indicating the person and everything remotely connected to him; since these translations all occur from a Semitic language, any claim of a specifically third-function intent is dubious.
The three words lev, nephesh, and meod, taken in a series, constitute a progression from the inner man to his outermost self. This is utterly different from the IE way of analyzing phenomena, and it should not be forced into or even toward IE categories, as it is in the Gospels, where mind, strength, and heart would appear to represent the three IE functions...
--- The Trinity and the Indo-European Tripartite World-view ---
http://www.tdl.com/~app/trinity.html
Here's another subtle example of the "1- 2- Many" structure found in the triadic arrangement of work days used by some businesses, particularly fastfood restaurants:
- One day = Sunday open 10AM to 6PM.
- Two days = Friday and Saturday open 9AM to 2AM.
- Many days = Monday through Thursday open 9AM to 10PM.
Researchers of infant babbling will often describe chunks (reduplications) of one, chunks of two, and then the developmental beginnings of words. In the word usage stages of development, they often describe one word usage, two word usage, and then an explosion of words. In each of these instances of "scientific" analysis they are using a variation of the old one - two - many sequence without realizing it. However, a usage of three-patterned babbling sequences can be identified in the utterances of infants and three-patterned word sequences can be identified in the expressions of young children learning to speak a culture's language.
For some examples of infant babbling, see:
--- Language 3s page 1 ---
http://www.threesology.org/language-3s-3.php
Being able to talk about something may define understanding, suggests a counting study in tribal people without words for higher numbers":
Language may shape human thought ... suggests a counting study in a Brazilian tribe whose language does not define numbers above two.
Hunter-gatherers from the Pirahä tribe, whose language only contains words for the numbers one and two, were unable to reliably tell the difference between four objects placed in a row and five in the same configuration, revealed the study.
Experts agree that the startling result provides the strongest support yet for the controversial hypothesis that the language available to humans defines our thoughts. So-called “linguistic determinism” was first proposed in 1950 but has been hotly debated ever since.
“It is a very surprising and very important result,” says Lisa Feigenson, a developmental psychologist at Johns Hopkins University in Baltimore, Maryland, US, who has tested babies’ abilities to distinguish between different numerical quantities. “Whether language actually allows you to have new thoughts is a very controversial issue.”
Peter Gordon, the psychologist at Columbia University in New York City who carried out the experiment, does not claim that his finding holds for all kinds of thought. “There are certainly things that we can think about that we cannot talk about. But for numbers I have shown that a limitation in language affects cognition,” he says.
H.O.B. note: But, why a recurring three, or progressive 1, 2, 3 form of determinism? What originates this particular form of determinism? Why not a 4, 5, 6, 7, 8, 9, 10, 11, 12, ... etc., determinism? If we say the "three" is due to the triplet codon system in DNA/RNA, what then originated this form of determinism in DNA and RNA? Surely, there may well be an identifiable environmental influence with this pattern.
“One, Two, Many” The language, Pirahã, is known as a “one, two, many” language because it only contains words for “one” and “two” (whereas) for all other numbers, a single word for “many” is used. “There are not really occasions in their daily lives where the Pirahã need to count,” explains Gordon.
In order to test if this prevented members of the tribe from perceiving higher numbers, Gordon set seven Pirahä a variety of tasks. In the simplest, he sat opposite an individual and laid out a random number of familiar objects, including batteries, sticks and nuts, in a row. The Pirahã were supposed to respond by laying out the same number of objects from their own pile.
For one, two and three objects, members of the tribe consistently matched Gordon’s pile correctly. But for four and five and up to ten, they could only match it approximately, deviating more from the correct number as the row got longer.
The Pirahã also failed to remember whether a box they had been shown seconds ago had four or five fish drawn on the top. When Gordon’s colleagues tapped on the floor three times, the Pirahã were able to imitate this precisely, but failed to mimic strings of four of five taps.
H.O.B. note: this study didn't mention the history of enumeration in which there were other cognitive limits. The primitive peoples of antiquity might well have been different than the primitive peoples we of today encounter. Primitive peoples of the past exhibited the quantity one as a limit, and then two as a limit, and the one - two - many as a cognitive limit, with some peoples quite possibly having successive cognitive limits. In fact, out usage of a comma to mark the boundary between ones, tens, hundreds "and" thousands. The comma is indicating a cognitive limit just as does our usage when labeling clothing sizes. We have small, medium, large, but anything beyond large does not receive a new word, it receives a re-usage of the one, two, three in that we say X-large, XX-large, XXX-large. In other words, we use 1, 2, 3 "X's".
Babies and animals
Gordon says this is the first convincing evidence that a language lacking words for certain concepts could actually prevent speakers of the language from understanding those concepts.
Previous experiments show that while babies and intelligent animals, such as rats, pigeons and monkeys, are capable of precisely counting small quantities, they can only approximately distinguish between clusters consisting of larger numbers. However, in these studies it was unclear whether an inability to articulate numbers was the reason for this.
H.O.B. note: the word "clusters" is used while those in infant babbling research use the word "chunks". The usage of such groupings might well be a "determinism" factor.
The Pirahä results provide a much stronger case for linguistic determinism, says Gordon, because, aside from their language, they are otherwise similar to other adult humans, whereas there are many more factors that separate babies and animals from adult humans.
However, scientists are far from a consensus. Feigenson points out that there could be other reasons, aside from pure language, why the Pirahä could not distinguish accurately for higher numbers including not being used to dealing with large numbers or set such tasks.
“The question remains highly controversial,” says psychologist Randy Gallistel of Rutgers University in Piscataway, New Jersey. “But this work will spark a great deal of discussion.”
Journal reference:
Science Express
19 August 2004/ Page 1/ 10.1126/science.1094492
NewScientist.com
http://www.newscientist.com/
Numbers and Numerals
Anand Singh
Illustrations by Amarjeet Malik
--- 4 to 40 ---
http://www.4to40.com

We do not know when primitive man first began to use speech instead of sign language to communicate with his family and neighbors, but we do know that man used words for thousands of years before he learned how to set these words down in writing. In the same way, many thousands of years passed after man learned to name numbers before he began to use signs for these numbers - for example, to use the numeral 3 in place of the word three.
Men needed numbers and had to learn to count. Maybe it started when one cave man wanted to trade the saber-tooth tiger he had slain for his neighbour's three spears. Or maybe it started when a twelve-year-old cave man junior wanted to tell his brothers and sisters about the four hairy mammoths he had seen during the hunt.
At first, primitive man used sign language to indicate the number he wanted to use.

He may have pointed to the three spears in his neighbour's cave or to the slain sabre-tooth tiger at his feet. He may have used his fingers to indicate the number. Two fingers raised on one hand meant two whether he was talking about two spears, two sabre-tooth tigers, two caves or two arrow heads.
In everyday usage, we understand that a number is a word or a symbol which signifies a specific quantity and it is not necessary to define what we are talking about. For example, either "three" or "3" can refer to three airplanes, three pens or three school-books.
Some primitive men did not use numbers beyond two. Only a century ago, When explorers visited the Hottentots in Central Africa, they found that these people had only three numbers: one, two and many. If a Hottentot had three or more cows, even if he had 79 or 2,000, he would count that number as "many." Most primitive men counted up to ten, or the total number of fingers on their hands. Others counted up to 20, or the number or the number of fingers and toes.
When you count on your fingers, it does not matter whether you start with your thumb or little finger. Among primitive people, there were set rules. The Zuni Indians started to count with the little finger of the left hand. The Otomacs of South America began with the thumb.
As men became more civilized, they used sticks, pebbles and shells to write numbers. They set three sticks or pebbles in a row to show that they meant three. Others made notches in a stick or tied knots in a rope as a means of writing their numbers.
When did man first use numerals?
The earliest written numbers so far discovered were used in ancient Egypt and Mesopotamia about 3000 B.C. These people, living many miles apart, each independently developed a set of numerals. Their simple numerals, 1, 2, 3, were copies of the cave man's sticks or notches. It is interesting to note that in many of the numeral systems found throughout the world, 1 was written as a single stroke (like a stick) or as a dot (like a pebble).
Egyptian 
Babylonian 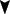
Early Roman Chinese Early Hindu Maya •


How did ancient man write?
The ancient Egyptians wrote their numerals on papyrus, a special paper made from reeds, painted them on pottery and carved them into the walls of their temples and pyramids. The Sumerians taught the Babylonians how to cut their numerals into soft clay tablets. The ancients Chinese did their number writing with ink and a bamboo brush or pen on cloth.
In the Western Hemisphere, with no contact with the rest of the world, the Mayas of Central America developed one of the most remarkable of the early number systems. They made their numerals using only three symbols: a dot (•), a straight line ( ___ ), an oval (
).
It doesn't take too much of an imagination to make the connection with these three and the list of linear- circular- triangular examples on the following page:
--- 3 "to" 1 ratios ---
How long would it take you to write a million?

The ancient Egyptians, Babylonians and Chinese, like the early Greeks and Romans, used special signs or numerals to express large numbers. This development of special signs for large numbers was the first advance in numeral writing. Imagine the difficulty and the time needed to write one million by cutting notches in branches or setting pebbles out in the sand. If you were to follow this method, or count pennies one at a time (1 a second), it would take you 278 hours, or 11 days and 14 hours of nonstop counting to reach one million.
Why are numerals important?
Every forward step in civilization brought additional uses for numerals. If a man owned land, he wanted to measure his property. If he sailed in his boat, be wanted to know how far from shore he was, if he wanted to build a temple or pyramid, he had to know how many stones he would need. When he learned to calculate with his numerals, he could measure time, distance, area and volume. By using numerals, he increased his knowledge and control of the world around him.
Updated Page Posting: Nov. 16, 2014
Your Questions, Comments and Additional information are welcomed:
Herb O. Buckland
herbobuckland@hotmail.com