~ The Study of Threes ~
http://threesology.org
Visitors as of 5/25/2021

Admittedly, I do not know how to write an equation which expresses a possible probability about the existence of a type of mathematics which does not yet exist in human conceptualization. Analogically speaking... for example, I am viewing myself (at this moment) in such a position as someone in the distant past who is adept at counting (with or without an abacus, or South American quipu cord), but has not even thought about the existence of multiplication, division, Algebra or Geometry, much less Trigonometry or Calculus.

Alternatively, I can visualize myself as a primitive human who has not conceptualized the usage of fire and the wheel, much less learned how to fashion even the simplest of tools... to say nothing of Agriculture or animal husbandry. Similarly, while we have evidence for the existence of atomic nuclei, no one that we know of has ever seen one. In at least one reference, that which is taking place within atoms has been referred to as a Giant Mystery hiding inside every atom of the Universe. We see effects, shadows and photographic trails, but these suggest we are seeing types of distorted refractions, reflections and diffractions. Yet despite the shadows by which we attempt to navigate reality, mathematical models reflecting such echoes reverberate oscillations of thought into cascading impressions whereby mathematical models help us to predict the possibility of something existing based on the probabilities created by an equation. Unfortunately, our mathematical models do not provide us with a visible spectrum of futuristic math equations waiting to be created through discovery. Such equations typically arise after a non-mathematical model is perceived as a phenomena. Math can be especially terrible at providing us insight into mathematics, as if it were a developing organism awaiting to blossom out of a cocoon or through some other process of maturation.
Whereas we create mathematical approximations which we come to "tweak" into useful caricatures of expression which assists us in making a discovery that might otherwise have remained hidden— and come to rely upon such portraits to provide different (probabilistic) landscape scenarios; there is a decided limitation to human brain activity within the confines of Earth's influences. Mathematics can create the illusion of limitlessness wherein fact it acts as an embellishment of the human ego wanting to experience limitlessness where none in fact exists. The fact that the Earth's rotation is incrementally deteriorating (along with the Sun burning out and the Moon receding); the human species, like so many other biological organisms, is forced to adapt to the deteriorations as a survival mechanism. These adaptations rely on a serviceable aptitude for rationalization. We see this in religion (theological/spirituality theories), political theories, economic theory, scientific theories, education theories, etc... Likewise, let us add mathematical theory to this list of rationalizations.
Nonetheless, mathematics affords us with some representations of predictability, so long as we remain in the intellectual parameter akin to a board game played with specific rules. Sometimes these rules are called Natural laws or in the case of general maths activity, they may be referred to as axioms derived from the compilation of assumptions and beliefs. Mathematicians tend to be adept bean counters whose egos thrive on the notion that Mathematics is viewed as the Queen of symbolic thought processing, and would not like to be viewed as a knave or domestique (domestic); much less an indentured servant.

Mathematics, viewed as a conceptual individual and not merely as a tool by which a form of conceptualization can be realized to provide consistency, has difficulty in predicting its own behavior which does not correspond to a required set of rules within the confines of a space and time of countable dimensions such as the length and width of a chess/chess/Parcheesi board, roulette wheel, or sports playing domain (football field, baseball diamond, basketball/tennis court, etc...). Static (linear) mathematics is particularly unable to provide a reliable measurement of a dynamic model of mathematics because the latter can be, like so many a creative thinker... quite unpredictably original... particularly in the inability of linear (static) equations to describe a new branch of mathematics. Linear mathematics is like a village idiot (that has been permitted to be the dominant in-breeder) who plays the role of an Igor that assists a mad scientist genius whose thought processing thinks circularly or in some other geometric form, mix and match as one might according to a given task.
It is not a fact but a rationalization to say that Mathematics is the Queen of all intellectual activity. It is also a rationalization to state that all sentient beings existing in the Universe will recognize human-created mathematics as a Universal language with which to use as a medium of communication. As if it were a lingua-franca or even the:
- Rosetta stone (3 languages:)
- Hieroglyphs (suitable for a priestly decree)
- Demotic (the native Egyptian script used for daily purposes, meaning 'language of the people')
- Ancient Greek (the language of the administration)
- Behistun Inscription (3 languages: Old Persian, Elamite, and Akkadian)
- Galle Trilingual Inscription (3 languages: Chinese, Tamil and Persian)
(As an aside note, the three languages and their usage have a flavor of exhibition reminding me of George's Dumezil's Tripartite Ideology, sometimes described as the Trifunctional hypothesis which can be used as a means for identifying a linquistic dimension of cognitive behavior that can be quantified and therefore numerically labeled.) However, just because Dumezil defined a given parameter of examination with specific labels does not mean later researches need to abide by a strict adherence to his criteria. Even originators of ideas can misinterpret aspects of observations with corresponding mis-labelings.


However, in contrast to the usage of three languages (patterns-of-three), we find an enormous reliance on patterns-of-two which can alternatively be labeled as opposites, contrasts, dichotomies, complements, complimentarities, etc., which can be reviewed here: Simplistic Dualities and Mathematics. In short, we see a difference in cognitive behavior that can be numerically assessed to further analogical comprehension by resorting to the historical reference of early counting efforts, where the phrase "1, 2, Many" can serve as a model describing the cognitive starts and stops. A dominant reliance of two-patterned ideas (and their multiples) gives the impression that the current stage of mathematical development is appreciably stuck in a "2" stage of reality perception; like a quadratic-wheeled vehicle stuck in the mud/muck spinning its wheels. Mathematics is hung up. It has remained for so long in its current bog that duration in the pit has bred generations of mathematicians that have adapted to the currency of perceptions afforded by such a purview, and developed tools by which to make their stay an accommodation. Like a person who has been born into an environment where the abacus is the greatest technological advancement of mathematical computation available, generations of mathematicians have become quite adept at using the prevailing tools and declaring them sacrosanct; because they never leave their quadratic vehicle and attempt to sojourn to the top of the rim of the pit they are bogged down in. Indeed, many of them do not even realize they are trapped, and assume that their existence is the best to be realized. That their reality is THE reality and the greater truth.
Note: in the history of counting, archeologists came to define the early instruments of accounting as a (bamboo/wood/ivory/bone/metal) stylus (as a type of writing instrument) and (clay/wax) tablet (as a type of writing surface). The terms "stylus" and "tablet" are not 21st century adaptations of these terms attributed to ancient artifacts. In other words, those in the past did not necessarily use these terms. I mention this because at the end of the article The Abacus: A Brief History, the author states:
"In the 21st century, portable counting devices rarely exist as separate entities. Instead they are simulated as Apps running on desktop computers, smartphones and tablets. Civilization, which began recording history with a stylus and a clay tablet thousands of years ago is re-using those original terms today."
The origin of the word "stylus" occurred in the 18th century and the word "tablet" has a Middle English origin. It is the idea of a stylus and tablet which are being reused, not the terms. The article can be interpreted to mean that the terms are as old as the artefacts themselves. A distinction is warranted... just as a distinction is warranted in viewing mathematics as a type of philosophy whose ideas can be enumerated to reveal a recurring cognitive profile expressing a simple counting sequence.
Mathematics has been used to illustrate the possibility of one or another substance, entity, idea, etc., that exists when typical observations do not lend an easy perception thereof. But a reliance on Mathematics as a... or THE tool for attenuating perception and ideas is a fallacy in that Mathematics lacks the ability to be predictive about the existence of a Mathematics which is being overlooked by the very many millions of people engaged in the serious usage of Mathematics as an analytical tool. Ideas which come to develop a new insight do not always use mathematics as a means to shine a light on every idea which assists humanity to step forward in conceptualization for the purpose of establishing a greater truth... a more far reaching appreciation beyond the established conventions of consideration. By trying to use mathematics, as it is presently expressed, as a presumed Universal language, the elements of mathematics with the conventions of language presents us with problems as described in this context: The Language and Grammar of Mathematics. Unraveling mathematical concepts as an expression of cognitive behavior which can be itemized in a numerical form, brings us to the situation in which we need to identify expressions in a numerical frame of reference on a basic level. We can do this by describing the three-part descriptive of Mononomial- Binomial- Polynomial, which is a clear approximation of the early counting notion of 1- 2- Many, except that detractors of such an alignment might want to point out the existence of other more-than-three structures in mathematical thinking. However, like the recurring usage of a two-patterned language used in computers due to our reliance on the on/off switching phenomena more often called a binary formula or language, though some are searching for the next stage of computer design using a ternary (or trinary) formula.
Distinguishing the presence and frequency of 1, 2, 3... and alternative patterns, however they may be described (with numbers, words or other symbols), is a means of referencing human cognitive behavior. Philosophers have long noted the frequency of using particular patterns of thought by describing them as a set illustrated with the word "Monad- Dyad- Triad". In fact, it is not too infrequent to find a philosopher in one subject context or another, using a particular pattern with which to assert a given idea. For example, Charles Sanders Peirce and his (three-patterned) theory of signs, though other thinkers are credited with having developed a comprehensive idea involving three references or establishing an idea which later became referenced with a pattern-of-three idea or phrase, though this says nothing about those ideas which prefer to reference some other underlying quantitative alignment:
| St. Augustine's Philosophy: | Memory~ Understanding~ Will |
| Comte's Philosophy: | Great Being ~ Great Medium ~ Great Fetish |
| Hegel's 3 Spirits: | Subjective Spirit ~ 0bjective Spirit ~ Absolute Spirit |
| Plotinu's Philosophy: | One ~ One Many ~ One and Many |
| Aristotle's 3 Unities: | Unity of Action ~ Unity of Time ~ Unity of Place |
| Sir F. Bacon's 3 Tables: | Presence ~ Absence ~ Degree |
| Thomas Hobbes's 3 Fields: | Physics ~ Moral Philosophy ~ Civil Philosophy |
| Immanuel Kant's 3 Critiques: | Pure Reason ~ Practical Reason ~ Judgment |
| Averroes's 3 Commentaries: | Little ~ Middle ~ Great |
| Karl Marx's 3 isms: | Communism ~ Socialism ~ Capitalism |
| Woodrow Wilson's 3 isms: | Colonialism ~ Racism ~ Anti-Communism |
| Hippocrates's Mind Disorders: | Mania ~ Melancholia ~ Phrenitis |
| Emile Durkeim's 3 Suicides: | Egoistic ~ Altruistic ~ Anomic |
| D. Liesman's 3 Social Characters: | Tradition-directed ~ Inner-directed ~ Other-directed |
| Erich Fromm's 3 Symbols: | The Conventional ~ The Accidental ~ The Universal |
| Pythagoras's "fusion" idea: | Monarchy ~ Oligarchy ~ Democracy (into harmonic whole) |
| M.L. King Jr.'s "Middle Road": | Acquiescence ~ Nonviolence ~ Violence |
| Kierkegaard's 3 Stages: | Aesthetic ~ Ethical ~ Religious |
| Husserl's 3 Reductions: | Phenomenological ~ Eidetic ~ Religious |
| St. Augustine's 3 Laws: | Divine Law ~ Natural Law ~ Temporal, or positive Law |
| Witness Stand "Laws": | Tell the Truth ~ The whole Truth ~ Nothing but the Truth |
| Titus Carus's 3 Ages: | Stone Age ~ Bronze Age ~ Iron Age |
| Feuerbach's 3 Thoughts: | God, 1st Thought ~ Reason, 2nd ~ Man, 3rd |
| Magnus's 3 Universals: | Ante Rem ~ In Rem ~ Post Rem |
| Max Weber's 3 Authorities: | Traditional ~ Charismatic ~ Legal-rational |
| F. de Sausure's 3 "Signs": | Sign ~ Signified ~ Signifier |
| Charles Pierce's 3 "Signs": | Qualisign ~ Sinsign (token) ~ Legisign (also, 1stness - 2ndness - 3rdness) |
| John Keynes's 3 Eras: | Scarcity ~ Abundance ~ Stabilization |
| George Mead's 3 Distinctions: | Self ~ I ~ Me |
| Thrasher's 3-group Gangs: | Inner Circle ~ Rank & File ~ Fringers |
| Abe Lincoln's 3-For-All: | Of the People ~ By the People ~ For the People |
| Jesus Christ's 3 Praises: | In the name of the Father~ Son~ Holy Spirit |
| Samuel Clemmons' 3 lies: (Mark Twain) |
Lies ~ Damned Lies ~ Statistics |
| Descartes 3 Kinds of Ideas: | Innate- Adventitious- Factitious |
|
Thesis ~ Antithesis ~ Synthesis Indulgence ~ "Middle Way" ~ Ascetism Major Premise ~ Minor Premise ~ Conclusion Contradiction ~ Excluded Middle ~ Identity Principal | ||
| "God-ology": Omnipresent Omnipotent Omniscient |
"Metaphysics-ology": What is real How change comes What is mind |
Marxian "Dialectology": Unity of opposites Quantity & quality Negation of negation |
| Epistemology: How we know What is truth What is mind |
Axiology: Nature of good Nature of beautiful Nature of religious |
Ontology: Quality (1st-ness) Relation (2nd-ness) Representation (3rd-ness) |
Then again, we can mention various ideas referencing a dominant pattern-of-two such as the Yin and Yang of the I-Ching, or the one-patterned concept of a single god; as described by the three large monotheistic religions labeled as Christianity, Islam, and Judaism... all three of which may be quite different today (if at all existing) if they had been developed in an other-than desert environment.

Cultural adaptations to an underlying recurrence of a standard cognitive model being herein described in a simple 3-part formula of 1- 2- Many, are being overlooked because the human ego embellishes the simple patterns into forms and formulations which conceal not only the patterns from many viewers, but that there is a recurrence of a limitation due to the ongoing incremental deterioration of the Earth's rotation, the Sun's energy, and the Moon's proximity... each of which participates in effecting environmental phenomena which affect the survival value of biological activity.
The Philosophy of Mathematics needs to be differentiated from the idea that Mathematics is a philosophy, as well as from the Philosophy and History of Mathematics. Whereas some conjecture that Logic is a word-label representation of a mathematic's-based formula of logistical considerations, let us view Mathematics as a symbolic model of philosophy... practiced in a framework of linguistics like playing a game that is guided by a set of rules in which a person is permitted to carry out certain operations of thinking to be stressed as the limits and in the example of chess; we note different pieces to be moved within the contour of the set parameters of the game and are not permitted to act on their own volition in the sense of inter-changeably using some other piece's ability to move in a given direction dictated by the three linear orientations of horizontal, diagonal and vertical. The present game of Mathematics has a set contour of symbolic expressions within the closed environment of the game board. As long as everyone abides by the rules, the game continues within the same types of playing moves until someone makes a cognitive leap and introduces a strategy (branch of mathematics) which becomes accepted as an allowable function permitted in some contexts by those players adept at thinking in a given way.
With respect to the I-Ching and its so-called eight symbols called trigrams, the trigrams are actually embellished bigrams masquerading as something beyond a pattern-of-two formula. It is the same currency of thought we find in mathematics as well. To be a true "trigram", the groups of three-line configurations would have to exhibit three different types of lines at the very least... consisting of one, two and three lines:

In the legal profession, there are quite a few embellished singular ideas called legal doublets which should be contrasted with legal triplets, all the while making note of the absence of lists referring to legal singularities, quadruples, quintuplets, etc... at least in the foregoing link but may be found elsewhere. In one context I found the topic of linguistic doublets being described as: The Historical Roots of Redundant Synonyms by Ken Adams, 20th April 2009, from which the following excerpt was taken:
...during the thirteenth century French replaced Latin as the primary language of legal expression and how during the fifteenth century law French was gradually replaced by law English.
The problem was: how can tradition be respected yet precision maintained when there are three languages competing for attention? It is plain that lawyers spend a great deal of their time worrying about the precise signification of words ... So what words should be chosen when Latin, French, and English each provide a copious supply of relevant items? How does one choose between synonyms, or—even more difficult—between two words which seem to be synonymous, but which might just have enough differential meaning to allow a lawyer one day to make an argument based on the difference?
The solution in many cases, was: don't choose; use both. In Middle English we see the rise of the legal lexical doublets which would become one of the stylistic hallmarks of that profession. Old English goods and Old French chattels resulted in Middle English legalese goods and chattels. The words were often paired to cover distinct nuances, thereby avoiding ambiguity; but sometimes the pairing seems to be no more than a more emphatic expressing of a single meaning; and sometimes it seems to be just a stylistic habit, perhaps fostered by its undoubted rhythmical appeal in oral performance. But whatever the reason, it became a major feature of legal style which continues to the present day.
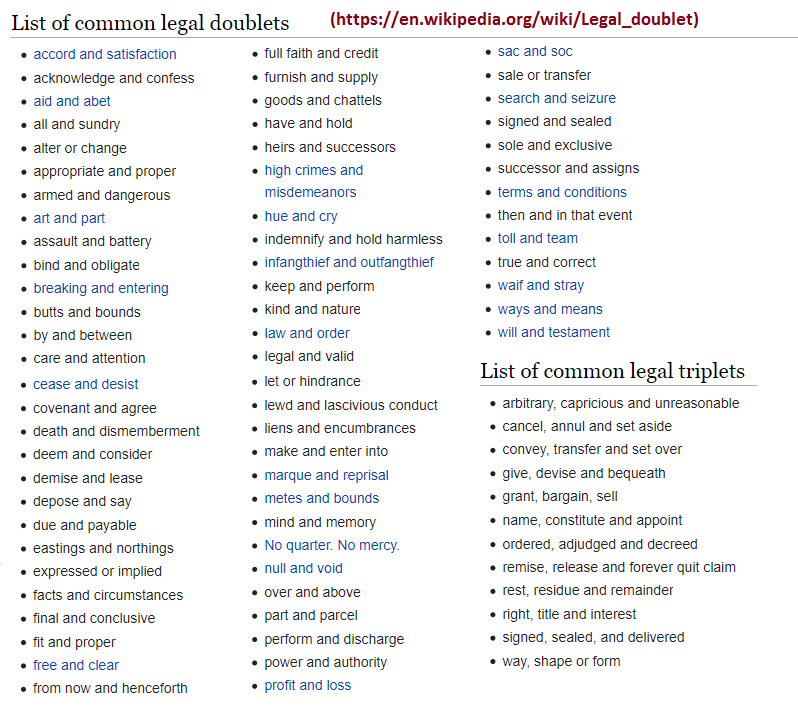
While one can speak of doublet synonyms, the idea of doublet antonyms can be introduced as an alternative perception of analysis, even though other values of comparison can be applied as well and then viewed in the context of analyzing mathematical ideas in a similar vein of orientation, all the while keeping in mind the idea that we can also identify quantity and that the overall quantity being used is limited... like an early counting scheme related to the development of human cognition within the context of an incrementally deteriorating environment.
Note: in the field of Biology we are confronted by a system of Taxonomy which uses a Binomial nomenclature:
In biology, binomial nomenclature is essential to integrate the naming system across life sciences and therefore assign one particular unique name identifier for a particular species across different languages. Binomial nomenclature is used especially by taxonomists in naming or identifying a species of a particular organism. It is used to come up with a scientific name for a species that is often based in Greek or Latin language. Although Latin is now a defunct language, the naming of organisms is still being used in this language.
The scientific name of a species that is set by binomial nomenclature entails two parts: (1) generic name (genus name) and (2) specific name (or specific epithet). In this regard, the scientific name is also referred to as the binomial name (or simply, binomial or binomen). The generic name is the taxonomic genus. A genus is a rank in the classification system that is generally below the family and above the species level. It is comprised of species with common attributes. These attributes may be based on structural similarities or on phylogeny. The second part of the binomial name is the specific name. In botanical nomenclature, the second part is particularly referred to as the "specific epithet". The second name (the specific name or the specific epithet) sets a particular species apart from the rest of the species within the genus.
...Although Carl Linnaeus was credited for the modern two-term naming system, his work was largely influenced by that of Gaspard Bauhin, together with his brother, Johann Bauhin. The Bauhin brothers were using the binomial nomenclature almost 200 years earlier. Many of the generic names introduced by them were adopted by Linnaeus.
The same sort of "embellishment tactic" is used in the binary world of computing when the Three basic Boolean operators are applied.
|
Boolean operators form the basis of mathematical sets and database logic.
Why use Boolean operators?
|
Because so much of everyday life has been fashioned under the auspices of an electronic industry "obsessed' with a pattern-of-two as a basic function of what we think is reality, we rationalize our world-view accordingly, and do not use the presence of the rationalization as a tool by which to comprehend the existence of being in a bog and spinning our wheels, cognitively speaking. It is a different set of two-patterned labels that we use then those of the ancient yin/yang variety, but it serves the same purpose of concealing the fact that we are accommodating to an on-going and enforced suppression of our intellectual capacity in order to accept the criteria by which we can maintain some semblance of equilibrium in an incrementally deteriorating environment.
While Mathematics is quite objective in many respects, it is like so many of us who become too close to a subject we lose objectivity. While being consumed ' with numbers, arithmetic, algebra, geometry, etc., may well afford someone to be "at-the-ready" for any possible introduction of a new perspective arising on the horizon of consideration, such a preparation can be singularly focused towards a given orientation; much like a soldier expecting an enemy to come over a certain ridge or along an expected path with this or that armament and with an accountable measure of fellow troops. Conventional linear mathematics inclines a Mathematician to think in predictable ways within a given guideline of expected conventional rights and wrongs. Engaging in the usage of conventional military tactics does not prepare one for originalities which are not configured in the usual equations.
Another problem with our mathematical models is in assessing the validity of the portrait being provided by ever-more complex models being generated by computers and mathematicians who give the impression of being like kids provided with ever larger boxes of crayons with multiple colors. Whereas smaller boxes with fewer colors of crayons provided for "black and white" representations, the uses of multiple tools, multiple equations, multiple configurations can lead to falsifications of existence and application. Whereas human imagination may run freely, such sojourns may not have applicability in the context of the present Earthly environment or even the larger galaxy nor be useful to humanity in its present state of biological design.
Here is one example of the foregoing realization with respect to mathematical modeling as a valuable asset:
Concluding Remarks
In this article, mathematical modeling concepts in relation to physical sciences, engineering, and technology have been surveyed. In recent years, mathematical modeling has pervaded all branches of knowledge, bringing forth greater understanding of processes under investigation. In engineering and technology it provides the analytical basis for design and control in which predictions can be confidently made without spending valuable resources of money and effort.
Successful applications of mathematical modeling techniques in engineering sciences have led the way to extend the techniques to more exotic areas of inquiry, like nanotechnology, nuclear-reactor engineering, material science, environment, weather prediction, biological processes, space sciences, cosmology, and also social sciences. Although the general philosophy of modeling in these new areas remains the same as discussed in this article, the simulation procedures and validation criteria are different and dependent on the types of models and the disciplines they belong to.
Mathematical modeling is a vast, multidisciplinary field that pleads to engage the interest and dedication of engineers, scientists and mathematicians to solve the problems facing the humankind. A significant development in the mathematical modeling activity is the availability of very-high-speed computers, which can solve a variety of complex models. In spite of all the advances in empirical knowledge, solution techniques, and computer assistance, it must be noted that human intelligence, experience, and intuition still play a significant role in mathematical modeling.
Mathematical Modeling by Xavier J.R. Avula, in Encyclopedia of Physical Science and Technology (Third Edition), 2003
Here is a second example:
Advances in computing hardware and algorithms have dramatically improved the ability to simulate complex processes computationally. Today's simulation capabilities offer the prospect of addressing questions that in the past could be addressed only by resource-intensive experimentation, if at all. Assessing the Reliability of Complex Models recognizes the ubiquity of uncertainty in computational estimates of reality and the necessity for its quantification.
As computational science and engineering have matured, the process of quantifying or bounding uncertainties in a computational estimate of a physical quality of interest has evolved into a small set of interdependent tasks: Verification, Validation, and Uncertainty of Quantification (V-VUQ). In recognition of the increasing importance of computational simulation and the increasing need to assess uncertainties in computational results, the National Research Council was asked to study the mathematical foundations of V-VUQ and to recommend steps that will ultimately lead to improved processes.
Assessing the Reliability of Complex Models: Mathematical and Statistical Foundations of Verification, Validation, and Uncertainty Quantification
Here is a third example of mathematical modeling in a given context for biological considerations:
Abstract
We discuss to what extent disease transmission models provide reliable predictions. The concept of prediction is delineated as it is understood by modellers, and illustrated by some classic and recent examples. A precondition for a model to provide valid predictions is that the assumptions underlying it correspond to the reality, but such correspondence is always limited—all models are simplifications of reality. A central tenet of the modelling enterprise is what we may call the ‘robustness thesis': a model whose assumptions approximately correspond to reality will make predictions that are approximately valid. To examine which of the predictions made by a model are trustworthy, it is essential to examine the outcomes of different models. Thus, if a highly simplified model makes a prediction, and if the same or a very similar prediction is made by a more elaborate model that includes some mechanisms or details that the first model did not, then we gain some confidence that the prediction is robust. An important benefit derived from mathematical modelling activity is that it demands transparency and accuracy regarding our assumptions, thus enabling us to test our understanding of the disease epidemiology by comparing model results and observed patterns. Models can also assist in decision-making by making projections regarding important issues such as intervention-induced changes in the spread of disease.
Mathematical modelling and prediction in infectious disease epidemiology by A. Huppert and G.Katriel
The usage of mathematical models to predict history (for example: Mathematicians Predict the Future With Data From the Past), or applied in a given type of biologically-directed analytical effort (for example: The Role of Mathematical Models in Understanding Pattern Formation in Developmental Biology by David M. Umulis and Hans G. Othmer); conceal the problem of mathematics as a tool towards understanding mathematics itself. Simply put, it is not being used to be predictive of the next stage of mathematics which is perceivable if a mathematical model afforded us the means of directing our attention towards a specific star of realization, instead of distracting us by all the star-like applications to which different mathematical forays are being applied. Whereas there are many pretty stars and interesting phenomena that one may focus on and comment about... if not write a book or thesis about, such items pale in comparison to the so-called once-in-a-life-time observations of a recurring event... such as when Haley had a comet named after him.
Halley's Comet is arguably the most famous comet. It is a "periodic" comet and returns to Earth's vicinity about every 75 years, making it possible for a human to see it twice in his or her lifetime. The last time it was here was in 1986, and it is projected to return in 2061.
The comet is named after English astronomer Edmond Halley, who examined reports of a comet approaching Earth in 1531, 1607 and 1682. He concluded that these three comets were actually the same comet returning over and over again, and predicted the comet would come again in 1758.
Halley didn't live to see the comet's return, but his discovery led to the comet being named after him. (The traditional pronunciation of the name usually rhymes with valley.) Halley's calculations showed that at least some comets orbit the sun.
Halley's Comet: Facts About the Most Famous Comet by Elizabeth Howell
Simply put, some mathematical equations are used periodically more often than others, and even have a specific name or moniker attached to them... thus enabling some people to sound intelligent by their ability to name several types of laws, rules-of-thumb or equations, though they themselves may never actually make active usage of them other than in the recitation thereof. While mathematical models can be highly useful in predicting the 'possible' existence of (for example) a given atomic particle or the presence of an object because of observed perturbations which occur in the presence of a known phenomena, mathematical modeling does not easily lend itself to be used as a tool to predict the existence of a new branch of mathematics without resorting to information which is used in mathematics but may not necessarily be viewed as being mathematical when observed outside the context of a mathematical application.
While some may argue that mathematical models are specific generalities or specific approximations, such expressions lend themselves towards being interpreted as educated guesstimations. Nonetheless, what I am describing is the present usage of mathematical models in an effort to predict further mathematical models themselves. Using a mathematical model to predict the possible evolution of mathematical modeling or a new branch of mathematics is not a convention of current thinking when thinking about mathematics as a developmental entity of cognitive activity arising from a biological organism that is said to be able to evolve. In other words, is the present state of Mathematics all there is? Is there to be no further development which is a distinct evolutionary step forward instead of just another branch or leaf or piece of fruit growing on the same tree planted centuries ago?
How do we write an equation for a mathematical idea that does not yet exist, or exists only in the framework of an idea generated by material from areas of research not typically described as being related to mathematics? Did mathematical models exist to predict the advent of double-entry accounting or the development of life from whatever genesis one subscribes to? When I ask if a mathematical existed, did it exist even though no human was aware of it? For example, did Algebra exist prior to human discover and usage? If we say that the geometry of the planets existed long before the advent of humanity and that humanity only discovered that which pre-existed the ability to conceptualize geometry, is this true for trigonometry, Calculus and else-wise? If we say that biology existed before humanity became aware of it, does the usage of a biological model afford us greater insight into the existence of non-biological activity such as the behavior and development of atomic nuclei? Does the behavior of mathematics follow a biological model, though we may not be privy as to what model of biology most nearly approximates mathematical activity and application?
How does one write an equation for a branch of mathematics which does not exist in present day usage, but exists on the horizon of a perception based on the collection and collation of information which can easily lend itself to mathematical probabilities? Like a primitive human whose mind may have been (unknowingly) exercising a counting sequence expressed in grunts (such as for example: ugh, ugh-ugh, ugh-ugh-ugh), how are they or someone nearby, come to illustrate such a series of expressions if their hand-to-eye coordinated symbolic usage was limited to three separate images (such as a line, circle, triangle), which did not appear to provide a similar three-part sequence as the vocal expressions? If the vocal expressions are viewed as a type of mathematical model and the three geometric figures as a different type of expression not characterized as a mathematical model, how can one make an intellectual correspondence if everyone is expecting the conventional model of express to be used in describing that which is possible in terms of human cognitive ability? If an extra- terrestrial uses different symbols and sequence of numbers than we humans, how can be rely on the language of mathematics to be a natural and universal language just because we describe it as such and expect all intelligent beings to understand what we believe to be a basic understanding of numerically symbolized reality? Needless to say, the philosophical underpinnings of human mathematics is problematic. Human mathematics may be little more than the survival strategy we see being employed by spiders in the construction of webs, or birds in the construction of nests, or bees in the construction of hives, or Chimpanzees in the usage of sticks to probe for insects, or colorful plumage to attract a mate, etc... Indeed, mathematics may be little more than an elaborate tail-feather display seen in peacocks. Whereas peacocks made pride themselves on their tail feather displays, and song birds in their songs, or deer in their antler rack, human mathematics has taken on a similar disposition.

If using a biological model for examining mathematics has merit (or a mechanical model, or a fluid model, etc...), is it too far-fetched to consider mathematics as existing in a primitive state of development awaiting a chance to evolve beyond its current obsessive usage of dichotomies, or move beyond the dichotomous back and forth movement of a mechanized Newton's Cradle (or Newton's Pendulum), or the non-steady state movement of some fluids which can be (in some conventions), viewed in terms of a dichotomy expressed as non-steady state versus Steady State: Unsteady State?
Is Mathematics unreasonably effective in the Natural Sciences, yet only reasonably effective in itself?
...Underlying the discovery of the Higgs boson is one of the truly great mysteries of modern science: why, in the physicist Eugene Wigner’s terms, is mathematics so unreasonably effective in physics? Or, as we might also ask, is mathematics the root of reality? Some physicists go further and say reality is the mathematics!
One can easily point to a long string of successes for mathematics. Beginning in the 1600s, Newton’s laws of motion and gravity, expressed in their true form as differential equations, succeed in explaining virtually every physical phenomena studied in science for the following 300 years.
In the late 1800s, the Scottish physicist James Clerk Maxwell showed mathematically that light was an electromagnetic wave. When he then calculated the speed of this wave, he obtained a value very close to the speed of light (299,792 km/sec or 186,282 mi/sec) that had been measured in careful experiments at the time. Those calculations in turn laid the foundation for Einstein’s special theory of relativity in 1905. Another of Einstein’s 1905 papers, on the photoelectric effect, laid the foundations for quantum mechanics.
In 1917, Einstein published an even more ambitious theory, the general theory of relativity, which implied the space-time continuum was curved in the presence of a massive object. Subsequent measurements of starlight bending around the sun dramatically confirmed these counter-intuitive predictions. In the following decades, physicists applied this theory to predict such exotic phenomena as black holes, as well as an initial singularity now known as the big bang.
Other physicists, extrapolating from the growing mathematical framework of quantum mechanics, predicted particles, and nature obediently produced these particles in experiments. Such examples barely scratch the surface – and the list goes on and on.
So perhaps it's not surprising the Higgs boson made its predicted appearance at the Large Hadron Collider (LHC) party, with exactly the properties earlier projected for it. Indeed, there is a deep fear in the physics community that the Higgs boson will prove to be so "ordinary" that no new physics will be glimpsed in the LHC. Is the Higgs the end of the line?
A Higgs, the Higgs … is maths at the root of reality? March 20, 2013 10:54 pm EDT
If we attempt to unravel the future of mathematics, do we invest time and energy in reviewing what we believe to be its earliest beginnings such as in the development of counting... eventually leading humans to develop the concept of zero? (How We Discovered The Number Zero Zero as a concept was something that didn’t always exist in human cultures. We had to find it for ourselves — more than once. by Nathaniel ScharpingJan 9, 2021 9:00 AM). Or does the origin of mathematics arise in a non-mathematical realm of expression such as art, whereby today some claim that mathematics is just another form of art? If present mathematics is a dialect of the assumed original beginning that did not reference any number at all, what then is the original language of mathematics and is there to be found a pristine realization that is otherwise "lost in translation" by those who have adopted the language(s) of mathematics to their particular interests? Is there a singular native tongue from which all the different dialects of mathematics arose? And if one discovers this pristine language, will it reveal a line of mathematically oriented thinking that can be developed into a far superior species of mathematics than any being used today?
Over the years, we have colloquially referred to mathematics as a special language. Yet practitioners have had little research to consult on the matter, or impetus to reflect on whether the process of learning the language of mathematics is similar to that of learning any other second language.
Although researchers have paid lip service to the unique vocabulary of mathematics, they have done little to highlight the ambiguities, double meanings, and other "word" problems associated with the discipline. Ignorance of these issues can lead to impaired communication at best, and serious mathematical misunderstanding at worst. To compound the difficulty, information in mathematics texts is presented in a bewildering assortment of ways; in attempting to engage students, textbook writers too often introduce graphic distraction, and format the pages in ways that obscure the basic concepts. In this book we look carefully and reflectively at the difficulties inherent in learning the language of mathematics, and suggest strategies for how best to overcome them.
There are over 4,000 languages and dialects in the world, and all of them share one thing in common: they have a category for words representing nouns, or objects, and a category for words representing verbs, or actions. Taking this commonality as a starting point provides an interesting way of looking at the mathematical world and its language. It is possible to identify both content and process dimensions in mathematics, but unlike many disciplines, in which process refers to general reasoning and logic skills, in mathematics the term refers to skills that are domain-specific. As a result, people tend to lump content and process together when discussing mathematics, calling it all mathematics content. However, it is vitally important to maintain a distinction between mathematical content and process, because the distinction reflects something very significant about the way humans approach mental activity of any sort. All human languages have grammatical structures that distinguish between nouns and verbs; these structures express the distinction between the objects themselves and the actions carried out by or on the objects.
Mathematics as Language by Joan M. Kenney
If we use a language model in which to describe mathematics, and resort to aligning concepts and patterns found in language to mathematics, then we need also to involve an appreciation of auditory processes related to the effort of distinguishing similarities of patterns. For example, language describes a universal usage of ordering that one may describe as a relative or family member to the sequences of numbers such as in counting 1... 2... 3, etc... With respect to linguistic typology, we find the three symbolic references of Subject- Object- Verb, whose arrangement occurs in a different order in different languages, but the same three values are used.
| Word order |
English equivalent |
Proportion of languages |
Example languages | |
|---|---|---|---|---|
| SOV | "She him loves." | 45% | 45 |
Ancient Greek, Bengali, Hindi, Japanese, Kannada, Korean, Latin, Malayalam, Persian, Sanskrit, Urdu |
| SVO | "She loves him." | 42% | 42 |
Chinese, English, French, German, Hausa, Hungarian, Italian, Malay, Russian, Spanish, Thai, Vietnamese |
| VSO | "Loves she him." | 9% | 9 |
Biblical Hebrew, Arabic, Irish, Filipino, Tuareg-Berber, Welsh |
| VOS | "Loves him she." | 3% | 3 |
Malagasy, Baure, Car |
| OVS | "Him loves she." | 1% | 1 |
Apalaí, Hixkaryana, Klingon |
| OSV | "Him she loves." | 0% | Warao | |
Mathematically speaking, if we take the dominant usage in the above table as our lead corresponding to the numerical values of 1, 2, 3 we have the values of numbers expressed as:

With respect to hearing and its importance to language, it is of value to delineate the recurrence of three-patterned structures, suggesting that a recurrence of some other quantitative pattern would influence a different type of language and concept formations. In other words, a language dependent mathematics would differ if the structure of the ear... and its necessity to hearing, had a dominant pattern that was other-than-three.
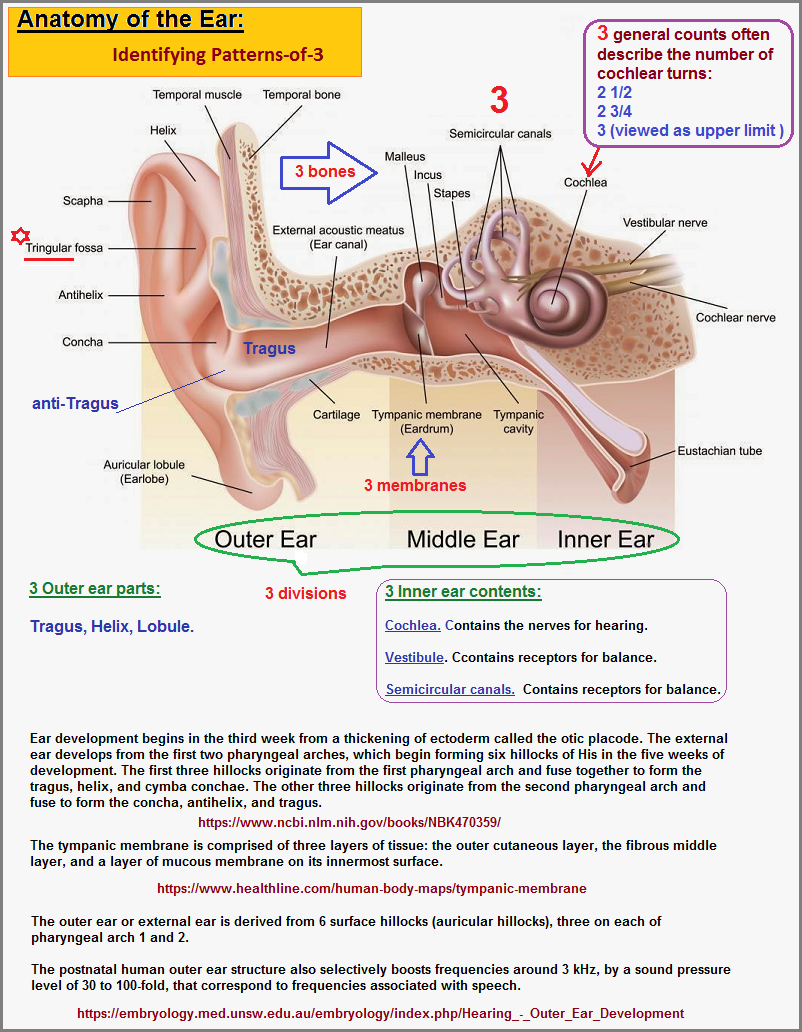
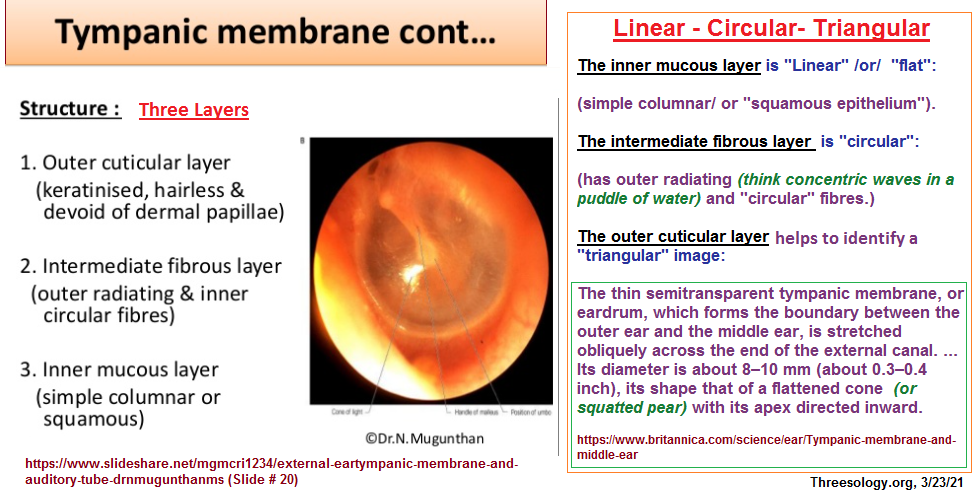
Further references: Language threes page 1
Page Origination: May 23rd, 2021...4:52 AM
Initial Posting: May 25th, 2021...8:47 AM
Updated Posting: May 26th, 2021...9:57 AM