~ 23 ~
~ The Study of Threes ~
http://threesology.org
Researchers as of 8/29/2019

| Devil's Advocate Series: | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14A 14B |
15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22A 22B |
23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 A | 30 B | 31 | 32 | 33a | 33b | 33c |
| 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 A | 41 B |
Very often in looking for examples of "three-patterned profiles", though there are occasions where a singular mention of "three" in one form or another is presented, I find an expression such as "2" or "two", or some other word or symbol referencing a quantity of two such as the binomial system of biological classification. Though it used to be when I was at a much younger age many decades ago I was preeminently interested in the primary pre-occupation of finding explicit examples of patterns-of-three, more intensive studying elicited the realization that a mention of "two" (in one symbolization or another)— and not only the "2" but other variables other-than-"3" as well— had a connection with a pattern-of-three.
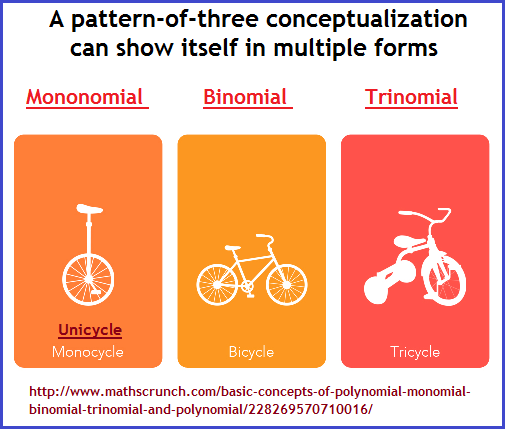
If the word "cycle" was not being used as a suffix and thereby not repeated, what then might we use to describe a one-two-three order, whether or not we also promoted the prefix arrangement as a enumerated progression? In making a cross-reference comparison, a short and simply survey reveals the following three examples of a human cognitive profile sampling:
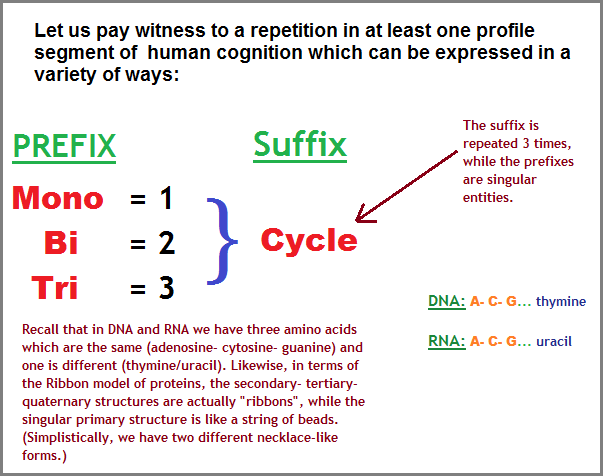
For example, while the hierarchical (top to bottom, and sexually oriented) classification system promoted by Carolus Linnaeus is described as a binomial nomenclature consisting of latinized descriptives for the different life forms denoted as a species as a guidance... as a tool... as a system of bookkeeping in arranging the two life form groups known as plants and animals and the one non-life form group designated "stones", that we of today more readily recognize as geology; the three of these comprised the then recognized three kingdoms of nature. (Today we recognize three basic types of rock based on how they are formed: sedimentary (layering), metamorphic, and igneous.) While such ideas were consistent during his time, and his idea of arrangement is in fact denoted as a Binomial classification system; it should be noted that there also exists a mono-nomial referencing within it to designate all ranks above species, though instead of the word "monomial" which more clearly indicates a quantity of one, the word "uninomial" is used. Hence, we had an initially proposed one and two qualitative naming occurrence. Yet, perhaps further unknown to some readers, a species may be divided into a sub-species, whereby some biologists adopt the usage of a trinomial nomenclature, and thus the species are designated as being polytypic (i.e. "many"... or more than two), as opposed to monotypic (referencing only one).
It should be noted that the classification system of 'stones' has had a rather rocky history: Animal, Vegetable, or Mineral? The idea of creating a “Tree of Minerals” seemed contrived, until recently.
Interestingly, in order to arrive at the conceptualization of a "binomial" system, it is composed of two singular parts, and is not expressed in a formula where there is a singularity and then a stand-alone 'bilarity'. In other words, it is a composite of two singles, which needs to be noted in order to appreciate the lack of complexity (or "innocence") (or "naiveté'") in the nature of the conceptualization being used:
Each kind of organism is known as a species, and similar species form a group called a genus. Each species has a scientific name in Latin that consists of two elements: the first is the genus and the second is the specific epithet. Together they are referred to as a binomial (literally - 2 names), and is always either italicized or underlined.
Binomial - the binomial is comprised of a genus and a specific epithet:
- Genus - the first word in a binomial, is always a singular noun, written with a capitalized initial letter - (for example: Rosa).
- Species - made up of 2 parts: genus and specific epithet. (for example: Rosa woodsii). Specific epithet is not capitalized (lower case).
The "species" is usually an adjective (for example: angustifolia, meaning "narrow-leaf") or named after a person (for example: walkeri), a commemorative, or place (for example: nevadensis, referring to Nevada). Although the generic name can be used by itself to refer to several species within the genus, specific names by themselves are not sufficient; they have no independent meaning, and cannot refer to a specific plant. E.g. "japonica" from 'Arbutus japonica', means only "Japanese". It does not refer to a particular plant. Many plants may bear the specific epithet of "japonica". Epithets, then, are meaningful only in combination with a generic name.
Trinomial - refers to the rank below that of species - subspecies or variety. A plant group can be so different in the wild from the general species originally described, that it warrants a botanical variety classification below that of species. E.g. Buxus microphylla Sieb. and Zucc. var. japonica Rehd. and Wils., which is native to Japan, and Buxus microphylla var. koreana Nakai, which is native to Korea. “Var." stands for varietas, Latin for variety. These botanical varieties are sufficiently different to warrant unique names and authorities to distinguish them from one another.
Classification, identification, nomenclature
However, this mono-bi-trinomial nomenclature (three-patterned singularity) system of classification is not universally adopted. (And nor should it be, because it represents a primitive variation of a three-patterned cognitive orientation.)
It is clear to me that the "uninomial", "binomial", "trinomial" perspective in the standard so-called binomial classification system is an unrecognized cognitive exercise equivalent to the early historical events in which the development of words and number symbols designating quantity arose in a one, then two, and then eventually to a three... from which sprang early arithmetic, accounting and later exercises of what are describe as being more complex mathematics.
A review of the history of number concept development tells of a trail in which there were starting points, stopping points, and generalizations for larger group structures of which the idea of "one-two-many" is ideally suited for as a conventional expression. In other words, early peoples came to adopt the notion of singularity referencing the quantity of one (in their own language equivalent way) with a specific word and/or symbol such as perhaps a single notch carved on a rock or piece of bone. For whatever period it took for the mentality of a given human segment to migrate towards the adoption of a word and/or symbol for the value of "2", the intervening period between the 1 and 2 could have been either a short or long period during the transition. In any event, one might imagine that each developmental step in organizing one's thoughts around a quantity of one that was now surplused by a singular addition and corresponded to qualitative parts of the body (such as two eyes, ears, hands, feet, etc...), there existed a period of prolonged contemplation and exercised repetition for additional perceptions of greater quantities to gain a foothold in human cognitive structuring.
Whereas initially there was one, no doubt embraced as a moment of great realization to have a word or symbol which could reference such an idealization, then came an equally charged Eureka! moment when the idealization for a quantity of 2 presented itself in a symbolic form; though prior to this any quantity beyond the "one" was no doubt a territory without a label except for perhaps that tied to some natural occurrence such as the multitude of stars, birds, insects, though there initially existed no word or symbol to give reference to a count of 2— much like animals that are said to be able to count, yet we can not be certain such animals have a mental image for a "two" reference— they simply give 'we humans' the impression of being able to distinguish what 'we humans' designate as a given quantity. While there may have been a time when any quantity beyond two was designated as much, many or more... with or without a specific word or symbol to express this measure, it is any one's guess since this part of number development in the history of humanity is not particularly well recorded. That which we see being displayed in texts describing developments of enumeration are examples of much later developmental sequences involving multiple numbers, though such numbers may express various re-duplications of smaller numbers to make larger numbers... like the activity seen in the babbling of infants whose later expressions are multiple "re-duplications" (repetitions) of smaller "chunks" of babbled... and then word expressions.
As it is considered today, whether it is believed or not, there exists the idea that primitive peoples followed a course of number knowledge development in which they, in their own language equivalent way, had a word for the quantity "1", a word for the quantity "2", and any quantity beyond the 2 was considered "many". Whether or not this three-patterned idea is a made-up construct of later researchers who were born into a culture where patterns-of-three expressions where a common language exercise of everyday speech, or is a factual recounting of what occurred in the history of number-concept development for one or more ancient peoples, is an argument I don't care to belabor at this moment. The idea nonetheless serves to illustrate the point of development along a 1-2-3 scenario that is easily understood and stands as an acceptable reference to what we might devise as the trail by which humanity came to develop and use number quantities.
As a very ancient representative model in which the mindset of ancient humans was preoccupied with "two" but beginning a transition into the recognition of "three", we can provide the illustration of the ancient Chinese so-called "trigrams" which are actually bigrams masquerading as a "three" concept that has not been fully developed:
Thinking out-loud in a number-related-to-word sense while looking at the eight (so-called) Trigrams, we might come up with:
- Monad ["Moad"] = One (the first "line" symbol)
- Biad [or Dyad/Diad] = Two (the second "line" symbol)
- Triad = Three (the third "line" symbol)
In the above sense I am speaking of the order of arrangement of the lines and am not counting individual component parts which make up a single line. For example:
|
The first (Ch'ien) representation would be written: |

|
|
The second (Chen) representation would be written: |

|
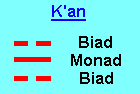
|
The third (K'an) representation would be written: |
|
Let's look at the list of 8 "Trigrams" with number symbol indicators instead of geometric symbols called lines:
Just like humanity's early attempts at number counting, there are many historical references to counting limits at the quantity two, one of which appears to be represented in the Chinese philosophy that is frequently referred to as the Trigrams. The developmental leap to the concept of "three" was frequently referred to as a representation of "many." (However, the development of number concepts as well as counting limits, in different places and times was represented by various symbols (including simple notches on sticks or stones).
|
Imaginatively, if we were so inclined to think in terms of Morse (or computer) Code, we could view the lines and spaces as either dots or dashes (or zeros and ones), whether or not we include the spaces between each successive line as either a dot or dash as well. And if you were further inclined to think of the so-called Trigrams as a secret code, a full Morse Code decipherment is awaiting some astute translator's disposition to unravel yet another great ancient Chinese secret... (mystery in metaphor). Just don't forget to mention my name in your book or movie that an indulgent public doles out millions for. But I would prefer not to be named after one of the Fast-food chains' give-a-way toys. |
A western interpretation which imposes the label of "Trigram," can lead to a misidentification of a "Trigram" philosophy that is actually a series of "Bigrams" that are striving for a Trigram identity. (A numerical concept of "two" that is advancing towards a numerical concept of "three.") Another example of a two-patterned perspective striving for a Three-patterned identity can be found in the (usually black/white colored) concept of Yin and Yang, which adopts the philosophical formula of Yin- Unity- Yang that a Western perspective might interpret to be a triad, but is actually a "biad" arrangement with an "intimation" of being a three-patterned structure. No less, we find another example of this when we look at the names of Asian gangs which espouse two-patterned references such as White Tigers, Red Dragons, etc., and yet are striving for an identity with a Triad organization.
The above excerpt from one of my earlier pages describes a similar condition with the "mono-nomial, bi-nomial, tri-nomial" exercise in the taxonomic system of biology. The system skirts the territory of a fully realized "three" orientation just like primitive peoples who skirted the development of a fully functional "three" from which followed arithmetic, accounting and eventually higher mathematics.
The point to be made in reference to the Binomial classification system used in biology, is that although the Uninomial and Binomial counts are appreciably used, the trinomial is in a transitional "to be used or not" stage of development. While the human brain is trying to wrestle with its own maturational development sequence in respect to changing environmental/social pressures where more and more (quantitative) requirements are being made on the human brain to contend with, just as primitive peoples were no doubt faced with the problem of having to tally larger quantities of animals, plants, events, etc., brought to the fore by an increasing quantity of interactive people in the social group; so too is the requirement of biologists to develop a classification system which accommodates an increasing array of information. Hence, humanity must move into adopting a "three" reference in the present binomial system of classification, but not in the manner which the first two (uninomial and binomial) are being used. The trinomial portion of a classification system is the end of the old and the beginning of the new, just as we make note of the fact that three number placements (such as ones-tens-hundreds) is the point of embarkation into a higher realm, a higher order of thinking separated by a comma. It is the system of referencing we see taking place in genetics as well, in that there are three stop codons and one start codon. The human brain appears to be exhibiting a similar orientation of three-patterned organization.
With this said, the "trinomial" part of the to-be-evolved taxonomic (binomial) system of classification must have its own identity, just as the first three numbers each have their own identity and do not exhibit the customary "th" when describing numerical placement beyond the third position:
1st2nd
3rd
4th, 5th, 6th, 7th, 8th, 9th, etc...
Hence, the adoption of a "threesological" perspective for the trinomial nomenclature is warranted; exhibiting a transition between a number word and an actual number value.
A threesological nomenclature involves both a reference to multiple "threes" biological occurrences, but also those events which lack a "three" and exhibit what appears to be another pattern in a recordable frequency, or lack there of.
Every single species has a functional number pattern to be used as part of the overall structure by which comparisons are being made. If species do not have actual assignable patterns identifiable by enumeration, then that which are being presently deduced, are arbitrary designations which have no place in a scientific system of classification. If we say that some perspectives of classification are just generalities, are just conveniences for the purposes of instruction, then we must contend with answering why only certain patterns are persistently being used.
The present binomial nomenclature is an image of an early formula of counting (encephalized accounting methodology) being expressed with a simplification that is sometimes confused as a tool by which the presumed complexity of biology is comprehensively unraveled from what might be describe as a knotted or puzzling configuration for which humans strive to unknot and piece together in a manner that is thought to be a means by which a holistic picture can be ascertained for the many (seemingly) disparate perceptions encountered in life.
With respect to the metaphor of a "knot" one might think of the term "Gordian knot," commonly used to describe a complex or unsolvable problem, which can be traced back to a legendary chapter in the life of Alexander the Great.
As the story goes, in 333 B.C. the Macedonian conqueror marched his army into the Phrygian capital of Gordium in modern day Turkey. Upon arriving in the city, he encountered an ancient wagon, its yoke tied with what one Roman historian later described as "several knots all so tightly entangled that it was impossible to see how they were fastened."
Phrygian tradition held that the wagon had once belonged to Gordius, the father of the celebrated King Midas. An oracle had declared that any man who could unravel its elaborate knots was destined to become ruler of all of Asia.
According to the ancient chronicler Arrian, the impetuous Alexander was instantly "seized with an ardent desire" to untie the Gordian knot. After wrestling with it for a time and finding no success, he stepped back from the mass of gnarled ropes and proclaimed, "It makes no difference how they are loosed." He then drew his sword and sliced the knot in half with a single stroke.
In another version of the legend, he simply pulled out a lynch pin running through the yoke, loosening the knot enough that he was able to unfasten it. Whatever method he used, the young king was immediately hailed as having outsmarted the ancient puzzle. That same night, Gordium was rocked by a thunder and lightning storm, which Alexander and his men took as a sign that he had pleased the gods. True to the prophecy, he went on to conquer Egypt and large swaths of Asia before his death at age 32.
What was the Gordian Knot? by Evan Andrews
One way in which humanity has addressed the "knotted" problems involved in making an account of different life forms, rocks, star clusters, weather patterns, cloud formations, human behavior, insect behavior, animal behavior, mechanical operations, atomic nuclei, etc..., is to formulate methods of categorization such as the binomial nomenclature system. Like a puzzle with a variety of pieces in which recurring methods of putting a puzzle together are used (such as arranging the edges, corners and look-a-like picture pieces first), humanity has very often resorted to varying practices of enumeration, even if the person describing a particular arrangement is not consciously aware that they are using some systemization which can be identified by others as having an underlying numbering system. As is often the case, the usage of an enumeration is not recognized because the words being used in the labeling system do not readily express some number value as do the words monocycle, bicycle and tricycle, or primary, secondary, tertiary, or any other intentionally used enumerated descriptive to identify a given difference by which a selection of elements or entities are being organized in reference to one another.
While the method of enumeration may appear to be reasonable or even highly logical, the problem is not in the offering nor usage of such a system, but in its retention as an absolute means of counting and giving an account of elements in a set way that becomes traditionalized and fixes the mindset of people for generations who do not come to appreciate the system as a primitive formula of counting by a particular profile of human cognition. The adopted system does not permit its own evolution though it may be used to identify and catalogue various models of evolution among its ranking and filing system. It is not seen as a species of human cognition itself. Nor is it reviewed in terms of being a simplistic model of a more complex ability waiting in the wings or backstage for its debut. It plays the part of an old actor who is sentimentalized into a state of adoration and deferment, that no new exercise talent is permitted to show itself... unless it is formed and functionalized into that which will best assist the old player in retaining top billing. Those who support the presently used binomial system and refuse to consider it as a primitive variation of human cognition, are much like those who have spent their lives in an accountant's position using a abacus, with which they are quite familiar and efficient with— able to defend their dominant accounting position against any would-be usurper using a different type of calculation machine within the scope of tackling problems that are drawn up by those who use the abacus method of accounting very well. By being able to define and create the types of problems to be addressed by the present currency of biology, the old accountants maintain their dominant positions. They are dismissive of any and all who attempt to introduce any new types of formulas for different types of problems their schooling and anointed contemplations shared amongst like-minded association-linked brethren regurgitate as a means of solidifying their positions and systems profiling methodology. They, like primitives, want to keep an old accounting system that they are most comfortable with, and not one which takes into account a larger array of information with an enlarged entourage of entanglements.
As should be noted, if an explicit "1-2-3" is not used, alternatives are sometimes employed that nonetheless express a cognitive pattern-of-three such as the mono- bi-/di- tri configuration, or a Uni- Duo- Poly, or various other formulations that may not even overtly express some representative enumeration, but still represent a pattern-of-three in the form... if not functionality of that being used as a system of labeling one's observations. This is not to say that a person isn't able to conceptualize in a larger numbering system, but that fundamental structures are often portrayed in groups of three or at least some lower number quantity that is less than or more than three... and should be interpreted as an overall limitation just as the triplet code in DNA is a recurring limitation.
If we look at the wikipedia's portrayal of the Linnaean classes for plants, in the Sexual System, we find the word "Icosandria" (flowers with 20 (or more) stamens, perigynous) and the word "polyandria" ( flowers with many stamens, inserted on the receptacle), both of which are obvious references to more than three, but are nonetheless represented values which are low, with respect to the large assortment of number values available (millions, billions, trillions, etc...). Such number values exceeding the "three" value do not refute the value of a threesological perspective which has helped to identify and outline recurrences of low number values and not high number values; thus representing a constraint which our minds are quite possibly affected by as well. Even though we use terms to describe a desire for unlimited ness such as diversity, multiplicity, dimension, freedom, liberty, etc., the usage of such words in all vocabularies are an overall expression of a limitation themselves. While some may use them to disguise the presence of recurring limitations and constraints, the fact that we can identify and should be cataloguing (in a systematic way) the present of recurring low (numerical) value concepts, details the presence of a taxonomic system to systematize all taxonomic systems whether so-named or otherwise. In several cases we see a pattern-of-two representing the "one-many" schema in the form of mono- poly, or in the case of America's E pluribus Unum cited as a motto of the Country's inception: it takes the form of the translation as: Latin for "Out of many, one" (also translated as "One out of many" or "One from many")... all of which are describing a three-to-one ratio previously mentioned on page 2 of this series and can rightly be added to the list on this page: Three "to" One ratios page A
- Classis 1. Monandria: flowers with 1 stamen
- Classis 2. Diandria: flowers with 2 stamens
- Classis 3. Triandria: flowers with 3 stamens
- Classis 4. Tetrandria: flowers with 4 stamens
- Classis 5. Pentandria: flowers with 5 stamens
- Classis 6. Hexandria: flowers with 6 stamens
- Hexandria monogynia
- Hexandria polygynia
- Classis 7. Heptandria: flowers with 7 stamens
- Classis 8. Octandria: flowers with 8 stamens
- Classis 9. Enneandria: flowers with 9 stamens
- Classis 10. Decandria: flowers with 10 stamens
- Classis 11. Dodecandria: flowers with 12 stamens
- Classis 12. Icosandria: flowers with 20 (or more) stamens, perigynous
- Classis 13. Polyandria: flowers with many stamens, inserted on the receptacle
- Classis 14. Didynamia: flowers with 4 stamens, 2 long and 2 short
- Classis 15. Tetradynamia: flowers with 6 stamens, 4 long and 2 short
- Classis 16. Monadelphia; flowers with the anthers separate, but the filaments united, at least at the base
- Classis 17. Diadelphia; flowers with the stamens united in two separate groups
- Classis 18. Polyadelphia; flowers with the stamens united in several separate groups
- Classis 19. Syngenesia; flowers with stamens united by their anthers
- Classis 20. Gynandria; flowers with the stamens united to the pistils
- Classis 21. Monoecia: monoecious plants
- Classis 22. Dioecia: dioecious plants
- Classis 23. Polygamia: polygamodioecious plants
- Classis 24. Cryptogamia: the "flowerless" plants, including ferns, fungi, algae, and bryophytes
The classes based on the number of stamens were then subdivided by the number of pistils, e.g. Hexandria monogynia with six stamens and one pistil.
Again, while researchers claim to being seeing one or another pattern and that the patterns are typically low in number value, does not automatically mean that which is being studied actually exhibits the pattern they are claiming, but may be whole or in part the result of a projected representation of a mental proclivity that all of humanity does not uniformally recognize as a construct similar to the development of a system of counting.
Origination date: Saturday, September 28th, 2019... 3:16 AM
Initial Posting: (Deming, NM) Wednesday, September 25th, 2019... 8:18 AM
Updated Posting:Tuesday, January 17th, 2023... 12:47 AM
Herb O. Buckland
herbobuckland@hotmail.com