(Static -vrs- Dynamic Equations)
10
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021

Let us now take a closer look a multiplicity of intelligences listing, which is undoubtedly known by many readers. While the list emboldens some readers towards thinking that they can now be included as having a significantly measurable intelligence and are therefore not left out of the reference made by those who wish to assert themselves as having a quality few others have, the overall list... when all supposed types of intelligence are taken into consideration, also displays a limitation... a cognitive conservation. Not only a limitation of the types of so-called intelligence, but a limitation of the human species' ability to create a label for different descriptions of intelligence. In other words, whether the list is one type, or ten, or 1,000... all these quantities express a limitation that is not being compared to the ongoing usage of limitations by human cognitive processing. The same think is occurring in mathematics. No matter how you jumble the numbers and symbols, the trend is towards an unrecognized conservation. Indeed, the idea of a one-god and infinity or even multiple universes all express an ongoing usage of an increasing conservatism being used by human thinking processes... and the reason(s) for this are not being taken into consideration for the well-being of any and all species.
In the following selection let me first recount the types of intelligences by Howard Gardner's theory: (Multiple Intelligences) and then next to it put a mathematically-centered twist to them; though one could just as well use any subject and do the same to indicate generalized-specificities within a specifically-generalized genre (and though such an ending expression may be interpreted as being humorous by some readers, I am actually pointing out an inherent dichotomy which can be exercised):
- Linguistic intelligence (“word smart”)
- Logical-mathematical intelligence (“number/reasoning smart”)
- Spatial intelligence (“picture smart”)
- Bodily-Kinesthetic intelligence (“body smart”)
- Musical intelligence (“music smart”)
- Interpersonal intelligence (“people smart”)
- Intrapersonal intelligence (“self smart”)
- Naturalist intelligence (“nature smart”)
- Linguistic mathematical intelligence (“word smart”)
- Logical-mathematical mathematics intelligence (“number/reasoning smart”)
- Spatial mathematical intelligence (“picture smart”)
- Bodily-Kinesthetic mathematical intelligence (“body smart”)
- Musical mathematics intelligence (“musical theory smart”) [music of the spheres: as in graphed geometrical alliances ]
- Interpersonal mathematics intelligence (“people smart”)
- Intrapersonal mathematics intelligence (“self smart”)
- Naturalist mathematics intelligence (“nature smart”)
In the foregoing list, some readers will not have any difficulty at all with recognizing the internalities of mathematical correspondences which occur along the separate types of labeled mathematical exercises.
In speaking to the development of a new model of calculation whose variables, enumeration, and symbols exist in a multitude of subjects with their respective languages, idioms, slang, and overall vernacular, it is of need to point out a very basic and generalized over-view of mathematics from its earlier beginnings as one might make an educated guesstimation of. For example: Before mathematics there was accounting. Before accounting there was simple counting. Before counting it is thought that some simple form of pairing or other association was being practiced... perhaps as nothing more than a doodling exercise.
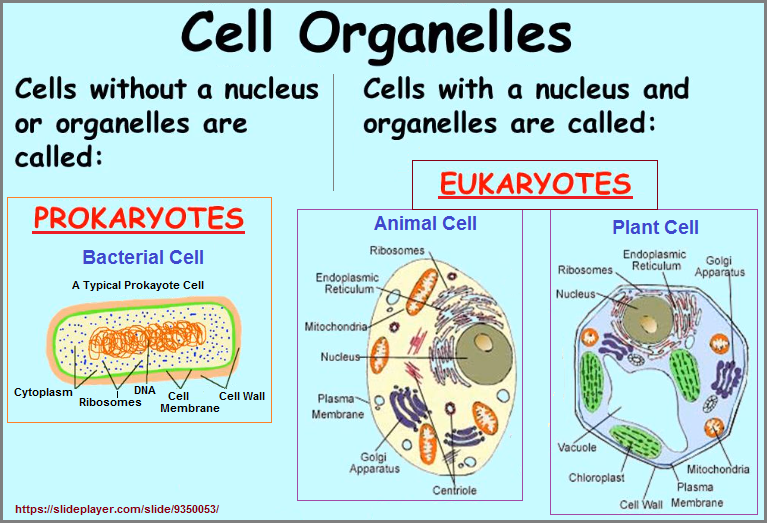
It reminds me of the early processes under-which a cell emerged with its compartmentalized organelles... by "friendly" aggregation and/or predatory capture... intentional or serendipitously.
Prokaryotes are organisms whose cells lack a nucleus and other organelles. Prokaryotes are divided into two distinct groups: the bacteria and the archaea, which scientists believe have unique evolutionary lineages.
Most prokaryotes are small, single-celled organisms that have a relatively simple structure. Prokaryotic cells are surrounded by a plasma membrane, but they have no internal membrane-bound organelles within their cytoplasm. The absence of a nucleus and other membrane-bound organelles differentiates prokaryotes from another class of organisms called eukaryotes.
Most prokaryotes carry a small amount of genetic material in the form of a single molecule, or chromosome, of circular DNA. The DNA in prokaryotes is contained in a central area of the cell called the nucleoid, which is not surrounded by a nuclear membrane. Many prokaryotes also carry small, circular DNA molecules called plasmids, which are distinct from the chromosomal DNA and can provide genetic advantages in specific environments.
prokaryote / procariote
Before simple counting there was collation (simple or by way of a "hoarding instinct"). Before collation their was collecting. Before collecting there was observation. Yet despite the foregoing approximations, let me attempt some model of itemization of these items in order to provide an inferentially associated reference, along with some instances of when they may have arisen in time:
- Observation: (millions of years ago) of natural phenomena such as low and high tides, night and day, hot and cold, stars, birds, life/death, young/old, etc...
- Collecting: (millions of years ago) rocks, leaves, shells, feathers, etc...
- Collation: (millions of years ago) into piles, pairs, singularities referenced by good/bad, weak/strong, important/not important, etc...
- Simple Counting: began around 50,000 years ago. (word/symbol? reference) 1 → 1 and many/heap/much/more; 1, 2→ 1 and 2 and many/heap/much/more; ... start- start, etc...
- Early Accounting: rudimentary number collections tied to early counting: Hence... A- (type of) counting.
- Astrology/Zodiac: Number, constellation (human/animal/month) pairing...
- Meso-American calendars: Zodiac? (Aztec, Incan, Mayan) 3 noted types:
- 260-day calendar, a ritual calendar with no confirmed correlation to astronomical or agricultural cycles
- 365-day period approximating the tropical year, known sometimes as the "vague year".
- Long Count is found in the inscriptions of several Mesoamerican cultures, most famously those of the Maya civilization who developed it to its fullest extent during the Classic period (ca. 200–900 CE). The Long Count provided the ability to uniquely identify days over a much longer period of time, by combining a sequence of day-counts or cycles of increasing length, calculated or set from a particular date in the mythical past. Most commonly, five such higher-order cycles in a modified vigesimal (base-20) count were used. Mesoamerican calendars
- Aztec Zodiac: (14th century? → origin of civilization
- Incan Zodiac: 12th to 15th centuries (Inca Astronomy)
- Mayan Zodiac: 2600 BC? → origin of civilization
- (List of pre-Columbian cultures... though the list of Mesoamerica excludes the Incas: List of pre-Columbian cultures)
- Babylonian (Mesopotamian): [12 months] 2000 BC Babylonian astrology
- Chinese Astrology/Zodiac: 5th century BC The Chinese Zodiac
- Egyptian Dendera zodiac... 2500 BC?
- West Eurasian peoples: 3000 BC... (History of astrology)
- Geometry: approximately 3,000 BC in ancient Egypt. (occurring sometime later after simple star-gazing. (Astronomy said to have arisen around 4th century BC defined by representations of planetary system.) From Star gazing arose sacred numbers like seven (7-starred Big Dipper, 7-starred pledges)...
- Later Accounting: single-entry accounting (300 BC) followed by double-entry accounting (1400s)...
- Algebra: 1600 to 1900 AD
- Calculus: late 17th century by Isaac Newton and Gottfried Leibniz.
Simply put, we can see the development or mathematics from simple beginnings, that are not routinely brought up in many articles about the history of mathematics, though this article does try to be a bit more objective in its considerations because it asks the question of where to start one's research in the history of mathematics: Early Counting Systems.
When we take stock of early counting methods, we come across stops and starts (like the one start and three stop codons found in genetics. For example, a person develops a symbol and word related to the quantity of one (1), and all other quantities may or may not have received a symbol (such as our infinity symbol). Thus, there is a stop at one. Next comes two with perhaps an associated symbol (such as perhaps a held-up finger) with a word. Then they stop here, which may or may not be associated with a concept for everything else such as heap, a lot, much, many, etc... Here is another cognitive stop. Next comes the concept of three with or without a corresponding symbol (other than with perhaps a held-up finger) and word... which may or may not be associated with a word and/or symbol for everything that is more than three followed by yet another cognitive step. Anyway, the point is that in the development of numbers, we shouldn't expect to see someone waking up one morning with the concept of numbers for 10, 100, 1000, etc., and their associated word/symbol references. Counting took time to develop. And yet, though cultures the world over learned to count and later develop mathematics which they may or may not have borrowed from other peoples, not every single practice developed an interest in "higher" math computations.
If we look at different interests which use numbers, and though the practice may have been around for centuries, the simple usage of numbers did not evolve into a mathematics. Take for example the zodiac. It retains a simple number ordering system aligned with numerically designated months, birth dates, etc., but its practitioners did not gravitate towards producing a formula of mathematics comparable to algebra, trigonometry and calculus. In other words, it retains a rudimentary form of counting and addition, though some basic geometry is attempted by charts of alignment. The same goes for business accounting. In short, we can find examples of using numbers in different types of practices, but they have not developed into a full blown exercise of mathematics. Indeed, we find that many inventions and activities do not use mathematics as a means of expression.
However, we have allowed mathematics to dominate the type of reasoning we have adopted in accordance with a preference for using mathematics as a measure tool of truth and logic, the lack of using mathematics can create conditions which deny a person to get their ideas across. Even though millions of people work out ideas by intuition and visualization by which useful creations are made, we have become so reliant on mathematics to define what is real, what is true, millions of people are denied a full expression of exhibiting their freedoms, to the extent some people don't try to exercise their "Eureka!" sparks of realization because society teaches everyone from elementary school on that if they can't express themselves, their ideas, their dreams in a mathematical way, they are unworthy of distinction. Mathematics is a type of enslavement and mathematicians... along with education systems, are the whip wielding task masters. You are viewed as being incapable of grasping higher concepts in anything unless it is accompanied by an astute comprehension of mathematics. Perhaps we need a system of higher education where mathematics is not permitted.
Like the old requirement of being able to read, write and speak Latin, Mathematics has become the new Latin requirement for knowing a foreign language, though other subjects are viewed as being just as strange by other students. (However, the difference being that if you don't know one or more of the other subjects you are not necessarily barred from entering into other courses.) Let's take a look at some examples of different great thinkers who either found mathematics a struggle, even distasteful, or whose ideas were dismissed as presenting some irrelevancy because the inventor or theorist couldn't read, write nor speak the language of "Mathematish": 6 Famous Scientists and Inventors Who Struggled With Math by Mark Mancini, Oct, 19, 2015
- Michael Faraday (1791-1867) In 1846, he boldly proposed that visible light is a form of electromagnetic radiation. But because he couldn't back up the idea with mathematics, his colleagues ignored it.
- Charlie Darwin (1809-1882) As a collegiate student, he loathed Mathematics. "The work was repugnant to me.”
- Alexander Gramham Bell (1847-1922) According to biographer Robert V. Bruce, Bell "enjoyed the intellectual exercise" of this subject, but was "bored and hence careless in working out the final answer once he learned the method." His grades suffered accordingly. Bell's mathematical aptitude never improved.
- Thomas Edison (1847-1931) "I can always hire a mathematician," Edison once remarked, "[but] they can't hire me." In his own words, according to one Thomas Edison biography, the book left him with nothing but "a distaste for mathematics from which I never recovered."
- Jack Horner (1946-Present) Horner's success must have shocked his childhood teachers. The Montana native did poorly in school, which he found "extremely difficult because my progress in reading, writing, and mathematics was excruciatingly slow."
- E.O. Wilson (1929-Present) ...2013's Letters to a Young Scientist—reveals a tumultuous personal history with math. The product of "relatively poor Southern schools," Wilson admits that he "didn't take algebra until my freshman year at the University of Alabama... I finally got around to calculus as a 32-year-old tenured professor at Harvard, where I sat uncomfortably in classes with undergraduate students only a bit more than half my age.
The Wright Brothers of airplane flight and Kittyhawk fame appear to have relied on date constructed by Otto Lilienthal of Germany and John Smeaton an English civil engineer. While history records the brothers using the data, it does not explicitly say how and in some reports, it is said that they thought lilienthal might be wrong. (The Wright Stuff: The Mathematics of the Wright Brothers by Robert N. McCullough. Other reports claim: "The truth of the matter is that it was not a problem of Lilienthal errors, rather it was a misinterpretation of his data that was the problem." Lilienthal Data not in Error by DR. Rchard Stimson. Whatever the case may be, an examination of their pocket-sized notebooks exhibit simple graphs and tables of trial and error efforts and do not admit to the usage of any exhaustive "higher" mathematics, perhaps owing to the fact that neither of the brothers went beyond high school and did not show a proclivity towards learning math beyond rudimentary skills. No less, their partner in the enterprise... their sister Kathrine wright was a school teacher, but with respect to math: Katharine excelled in most of her courses of study, with the exception of math. She met with a tutor three times a week and that tutor, Henry Joseph Haskell, would later become her husband.
When we attempt to discover the Mathematics used by Leonard Da Vinci, we encounter present day interpretations of his works in relation to our mathematical representations of his efforts. In other words, we do not see math equations, but illustrations of perspective, space, intuition, proportion and geometrical shapes. Let us be honest and don't try to embellish his works by describing them in modern terms just because we have some special affinity for mathematics. He didn't use mathematics as we today ascribe to it. People need to stop romanticizing that he (and other did). You don't hear of every artist today being described as a mathematician who use similar devices for constructing their works. Interpreting everything Leonard did in a mathematical framework is just as silly as those who believed they uncovered some hidden message in the dimensions of the pyramids, or obelisks, or hieroglyphics. However, what it amounts to is a confession that mathematical thinking, mathematical logic does not need so-called "proper" math expression called equations. It can be expressed alternatively, except that present day education is ramming "proper" mathematics as the only form that every child must have, without exception. Let us take a brief look at the development of mathematics during Leonardo's time (15 April 1452 – 2 May 1519):

The Super-magic Square
It is a tribute to the respect in which mathematics was held in Renaissance Europe that the famed German artist Albrecht Dürer included an order-4 magic square in his engraving "Melencolia I". In fact, it is a so-called "super magic square" with many more lines of addition symmetry than a regular 4 x 4 magic square (see image above). The year of the work, 1514, is shown in the two bottom central squares.
An important figure in the late 15th and early 16th Centuries is an Italian Franciscan friar called Luca Pacioli, who published a book on arithmetic, geometry and book-keeping at the end of the 15th Century which became quite popular for the mathematical puzzles it contained. It also introduced symbols for plus and minus for the first time in a printed book (although this is also sometimes attributed to Giel Vander Hoecke, Johannes Widmann and others), symbols that were to become standard notation. Pacioli also investigated the Golden Ratio of 1 : 1.618... (see the section on Fibonacci) in his 1509 book The Divine Proportion, concluding that the number was a message from God and a source of secret knowledge about the inner beauty of things.
During the 16th and early 17th Century, the equals, multiplication, division, radical (root), decimal and inequality symbols were gradually introduced and standardized. The use of decimal fractions and decimal arithmetic is usually attributed to the Flemish mathematician Simon Stevin the late 16th Century, although the decimal point notation was not popularized until early in the 17th Century. Stevin was ahead of his time in enjoining that all types of numbers, whether fractions, negatives, real numbers or surds (such as √2) should be treated equally as numbers in their own right.
In the Renaissance Italy of the early 16th Century, Bologna University in particular was famed for its intense public mathematics competitions. It was in just such a competition that the unlikely figure of the young, self-taught Niccolö Fontana Tartaglia revealed to the world the formula for solving first one type, and later all types, of cubic equations (equations with terms including x3), an achievement hitherto considered impossible and which had stumped the best mathematicians of China, India and the Islamic world.
The Story of Mathematics
Since mathematics is a made-up language, like runes, ideographics, Las Calle wall paintings, hieroglyphics, ancient Greek, Latin, Aramaic as well as the languages-laden vocabularies of all subjects (development biology, religion (the many sects of Islam, Bahai' faith, Christianity, Buddhism, Judaism, Mormonism, Shintoism, Jainism, Hinduism, Quakerism, etc...), evolution, politics, physics, sports, theater, warfare, etc..)— to include all cultures, archeological and paleo-anthropological artifacts, Astrology, Astronomy, Free-Masonry and Knights Templar symbology, etc.; let us also note that many of our subjects either grew up in an age where the existence of cult thinking and participation was a regularity defined by a small selection of individuals, or the traditions of cult-mindedness greatly influenced later ideas and ideals to re-enact internalized secrets and secrecy... which today may be defined by larger memberships due to an overall increased global population, and an exposure of secret activities which may be called entrance fees, learning fees and rituals with extensive memorizations, secret password or handshakes replaced by employee badges, dress codes, and multiple other language codes generalized into the two-part phrase of "Walk the walk and Talk the talk" (of the initiates in a given enterprise). In some cases such as street gangs and criminal activities, a person is expected to join for good, for life, or forever, or be confronted by a death sentence, severe ostracism, or other occurrences amounting to a life-long penance similar to the mental mood of those subjected to long-term stretches of incarceration which become minimized by inmates by having time equated with small denominations of money. For example, a five year sentence is viewed as a "nickel". A ten-year period is called a "Dime". Twenty five years is a quarter and so forth.
Mathematics, like religion, has been a successful cult. It has even managed to become a socially established requirement for all people to become proficient in at least in terms of simple or basic arithmetic. Religion has achieved a similar imposition on the public by establishing the idea of a supreme god, and that religion is the owner of such an idea as well as claiming itself to be the master of spiritual truth and overall human morality. But there are other cult-minded institutions such as the dominance of the word "Democracy" and "Capitalism". All politics and economic perspectives are cults. Albeit cults with millions of followers, but cults nonetheless.
With respect to Mathematics being viewed as a cult having its own practiced (living) speaking language, the requirement to learn its written language and language related symbology, is time and again found to be difficult for most people to learn the abstract language configurations, much less acquire a familiarity to write the language as required by a given 'sect' (such as the mathematics used in physics, population genetics, fluid mechanics, geometry, etc...). So, is this a problem with the larger public, or the smaller languages of mathematics? In other words, is mathematics at fault because it requires a type of memorization and twists of thought processing out-of-step with the conventions of what might be called a Standard Cognitive Model of thinking?
It is not uncommon to find someone who thinks that Mathematicians are like artists constructing artistic expressions or musical renditions in deliberately conjured-up contraptions called equations and musical scores in methods and manners suited for a specific audience with a given taste. In other words, Mathematics is looked like a speciality of appreciation that is being forced on the whole of the public to swallow like U.S. children of the past were forced by parents to bring regular spoonfuls of castor oil as if it were a universal preventative measure for multiple illnesses. Many, if not most math equations are being viewed as Picasso-like abstractions where a select few of interested people have a dominant sway on the overall interpretation of it s social usefulness... though many a Mathematician (for example, G.W. Hardy Of Ramanujan fame), hope their "Pure" mathematical expressions are never found to have a utilitary application, because they believe they are engaging in a superior form of math as if it were like a transcendent being that exceeds all realms of spiritual and philosophical species of body, mind, and soul.
Hence, to suggest we alter the speaking and written as well as feeling, thinking and intuitive characteristics of Mathematics by introducing the concept of a Dynamic (or dynamical) mathematics which a circle/sphere or a one/two-sided triangle, 3-sided (plus base) trihedron, or 4-sided (plus base) tetrahedron may be used to generalize an illustration thereof; may give the impression to some that such a task is the engagement in mere semantics than actually providing a means by which we are enabled to step into a new territory of mathematics expression suggested by the notion of a dynamic versus a static equation, (without intending to be interpreted as a combative stance)... the latter being a reference to the present currency of linear equations being used as two-dimensional configurations requiring an individual to supply visualized animations within the linear language vernacular (tongue).
And yet, if such a language as the linear is counter-intuitive, presenting multiple obstacles to many people as evidence by the larger public's aversion to learning the language because the memory techniques for embracing the language are themselves a difficulty of the language requirement, they are said not to be able to "see", to appreciate, to fully realize the supposed greater truth (like some who claim that a [particularized] "spiritual experience" is a requirement for someone being able to fully grasp their beliefs); because they are not expressing it in the required mathematical language nor thinking in the language. Hence, the refrain that "something is lost" in translation when the language is poorly understood and instead of being the urban legend compilation which it is, it is held up as some sort of definitive declaration which asserts the self-initiated validations of Mathematicians of a self-molded embodiment of presumed uniqueness that becomes an accepted standard traditionalized by a general public mood of an indentured obeisance to this view.
Being able to grasp (if not write and speak of) reality in the way mathematicians do, is more easily absorbed if one is subjected to a culture in which mathematics is the standard form of everyday communication. It is its own type of sanity... or if you prefer: it's own flavor of insanity. If you have ever been to a place of learning where everyone embraces the given language and beliefs of a particular subject, fanaticism is a common personality theme. For example, to attend a college where the dominant orientation is to a given religious belief, you might well find yourself in what you would otherwise describe as a psychiatric ward, where all perceptions are rationalized in terms of the dominant belief and conveyed in the dominant language used to convey the many different day-to-day life-skill narratives, songs, relationship communications, personal goals, self-denials, self-recriminations, group support networks, etc... If you don't believe in the religion, or your mind is not configured to play out a role in engaging yourself in what can be described as playing with a Rubicks' cube, you may well find yourself thinking everyone around you is insane, or that you are. Yep, Mathematics is its own insanity, despite its usefulness because humanity has thought up something better.
Beyond simple arithmetic... to include fractions, perhaps some decimals and basic graphs and geometry; is how most people live out their lives. While some may want to know more mathematics and even those who have a penchant for mathematics, the truth of the matter is that they carry on with what basic math skills they have and turn to the use of something else... such as words, or puzzle making, or cooking, or gardening or rebuilding a vehicle from the ground up, or becoming a self- or publicly noted- expert in one thing or another that does not involve math. For example, the work of plumbers, electrician's police officers, politicians, doctors, dentists, mechanics, delivery drivers, garbage collectors, fruit harvesters, etc., are not noted for their math skills.
Yet, each one of them may consider something they do is equivalent to higher... if not "pure" mathematics, albeit within the scope and with those implements characteristic of a given exercise, be it mental, emotional or physical... mix and match as you will. Indeed, do we claim that math is an expressed intelligence used by some as a tool, whereby math is discovered instead of being created? Or is it that someone creates it so that another may discover it at some time? In this sense it would be that the development of a new mathematics... as a new or different type of human conceptualization, emerges on the scene of human ability that may become mentioned to another who likewise is near enough the evolutionary change in mental development, that they to are led along the same or similar path and make note of it... and it is the note in the hands of one or more that gets tossed socially about "under the radar" of most conversations
Date of Origination: 26 February 2021... 6:59 AM
Initial Posting: 1st July 2021... 4:46 AM