(Static -vrs- Dynamic)
5
~ The Study of Threes ~
http://threesology.org
Visitors as of 2/27/2021

Let us take a look at a contemporary definition of Pure mathematics and see if you can't recognize its inherent flaw of philosophy being used as a standard adjudication of its probity and propriety for doing what it does in much the same manner as might an artist, musician or writing orientation when they claim they have a "poetic" or "creative" or "literary" license which cannot be revoked or otherwise the consequences for all of humanity will be devastating:
Pure Mathematics definitions: Pure mathematics is the study of the basic concepts and structures that underlie mathematics. Its purpose is to search for a deeper understanding and an expanded knowledge of mathematics itself. Traditionally, pure mathematics has been classified into three general fields:
Pure Mathematics definitions:
- Pure mathematics is the study of the basic concepts and structures that underlie mathematics. Its purpose is to search for a deeper understanding and an
expanded knowledge of mathematics itself. Traditionally, pure mathematics has been classified into three general fields:
- Analysis, which deals with continuous aspects of mathematics.
- Algebra, which deals with discrete aspects.
- Geometry. (MIT Mathematics)
- Pure Mathematics is both an art and a science, and pure mathematics lies at its heart. Pure mathematics explores the boundary of mathematics and pure reason. It has been described as "that part of mathematical activity that is done without explicit or immediate consideration of direct application," although what is "pure" in one era often becomes applied later. Finance and cryptography are current examples of areas to which pure mathematics is applied in significant ways. (What is Pure Math?)
- Pure mathematics is the study of mathematical concepts independently of any application outside mathematics. These concepts may originate in real-world concerns, and the results obtained may later turn out to be useful for practical applications, but pure mathematicians are not primarily motivated by such applications. Instead, the appeal is attributed to the intellectual challenge and aesthetic beauty of working out the logical consequences of basic principles. It follows that, presently, the distinction between pure and applied mathematics is more a philosophical point of view or a mathematician's preference than a rigid subdivision of mathematics. In particular, it is not uncommon that some members of a department of applied mathematics describe themselves as pure mathematicians.(Wikipedia: Pure Mathematics
- Pure mathematics uses mathematics to explore abstract ideas, mathematics that does not necessarily describe a real physical system. This can include developing the fundamental tools used by mathematicians, such as algebra and calculus, describing multi-dimensional space, or better understanding the philosophical meaning of mathematics and numbers themselves. (Pure Mathematics)
(The following is truncated from the actual article.)
What is pure mathematics? What do pure mathematicians do? Why is pure mathematics important?
Broadly speaking, there are two different types of mathematics —pure and applied. Philosophers such as Bertrand Russell attempted to give rigorous definitions of this classification.
What this means is that the paradigm in which mathematics is done by the two groups of people are different.
Pure mathematicians are often driven by abstract problems. To make the abstract concrete, here are a couple of examples: "are there infinitely many twin primes" or "does every true mathematical statement have a proof?"
- To be more precise, mathematics built out of axioms, and the nature of mathematical truth is governed by predicate logic.
- A mathematical theorem is a true statement that is accompanied by a proof that illustrates its truth beyond all doubt by deduction using logic.
- Unlike an empirical theory, it is not enough to simply construct an explanation that may change as exceptions arise.
- Something a mathematician suspects of being true due to evidence, but not proof, is simply conjecture.
Explainer: the point of pure mathematics Aug. 1, 2011 4.56pm EDT
In other words, they are like Bohemian artists and musicians pursuing the ever illusive epitome of artistic expression or the purest note... like any zealous participant in many different types of cultish practices.
It is a view which I had generated long before I read the following reference concerning G.H. Hardy's view of Pure and Applied mathematics:
Pure vs. Applied mathematics
Mathematicians have always had differing opinions regarding the distinction between pure and applied mathematics. One of the most famous (but perhaps misunderstood) modern examples of this debate can be found in G.H. Hardy's A Mathematician's Apology; (Wikipedia: A Mathematician's Apology).
It is widely believed that Hardy considered applied mathematics to be ugly and dull. Although it is true that Hardy preferred pure mathematics, which he often compared to painting and poetry, Hardy saw the distinction between pure and applied mathematics to be simply that applied mathematics sought to express physical truth in a mathematical framework, whereas pure mathematics expressed truths that were independent of the physical world. Hardy made a separate distinction in mathematics between what he called "real" mathematics, "which has permanent aesthetic value", and "the dull and elementary parts of mathematics" that have practical use.
Hardy considered some physicists, such as Einstein and Dirac, to be among the "real" mathematicians, but at the time that he was writing the Apology he considered general relativity and quantum mechanics to be "useless", which allowed him to hold the opinion that only "dull" mathematics was useful. Moreover, Hardy briefly admitted that—just as the application of matrix theory and group theory to physics had come unexpectedly—the time may come where some kinds of beautiful, "real" mathematics may be useful as well.
Another insightful view is offered by Magid:
I've always thought that a good model here could be drawn from ring theory. In that subject, one has the sub-areas of commutative ring theory and non-commutative ring theory. An uninformed observer might think that these represent a dichotomy, but in fact the latter subsumes the former: a non-commutative ring is a not-necessarily-commutative ring. If we use similar conventions, then we could refer to applied mathematics and non-applied mathematics, where by the latter we mean not-necessarily-applied mathematics... [emphasis added].
Pure Mathematics
My thinking about mathematics has obtained the creation of a generalized account where it evolved as a metaphor portrayed as thus:
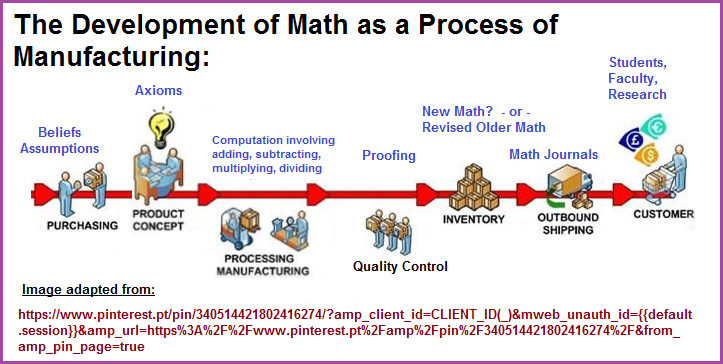
Assumptions became beliefs which were added together like variables to produce the sum labeled axiom. The developed Axiom(s) were then subjected to a box of machinery that can be analogously viewed as a warehouse with a production line along which raw materials are shaped (by way of addition, subtraction, multiplication and division) set up as an S.O.P. (standard operating procedure) called Order-of-Operations(PEMDAS: parenthesis- exponent- multiplication- addition- subtraction), out of which was fashioned a product called an untested truth whose quality needed to be proved as a worthy product.
This truth (as an end-product of the process) is then subjected to a Q.C. (quality control) series of examinations (frequently expressed as a mathematized syllogistic logic) from which is established a finished product presented as a real and true-to-life construct abbreviated into the singular trade name called reality.
And like any established "reality" developed from a processing system whose materials origin(s) are assumptions and beliefs transfigured into a model named axiom that creates an artificialized level of increased value; the reality can be altered by changing the initial materials, by a person altering the production process, or the philosophy attached to the Quality (Qualification) Control department.
However, one should note that this same production scenario takes place in all subjects, including the supposed equality of law, sports, entertainment... business..., religion, art, theater, literature, and other human endeavours where the production process is not necessarily as tuned-into a given subject matter's genre of melodic inter-facing as it is found in many academically oriented sojourns of research and development; despite commentary that someone has developed a science out of their proficiency in a given activity.
To provide one example of the production line model taking place in another context, perhaps one from biology will be sufficient:
Cell Organelles and their Functions| Organelle | Biological Function | Factory Part |
| Nucleus | DNA Storage | Files and blueprints management |
| Mitochondrion | Energy production | Powerplant |
| Ribosome | Protein synthesis | Machine to product toys |
| Rough ER | Protein production and modification | Coordination of toy production line and decoration |
| Smooth ER | Lipid production and Detoxification | Accessory production |
| Golgi apparatus | Protein transportation and export | Packaging and shipping department |
| Peroxisome | Lipid breakdown; redox reactions | Hazard chemical handling |
| Lysosome | Protein destruction | Recycling |
| Cytoskeleton | Cell movement; intracellular transportation | Conveyor system |
| Cell membrane | Define the inside and outside of a cell | Factory building |
| Cell wall | Structural support and protection (plant cell) | Reinforced factory building |
| Cytosol | Cellular fluid | Internal space and floor plan |
| Chloroplast | Photosynthesis (plant cell) | Solar panels |
| Vacuole | Storage and water regulation (plant cell) | Storage spaces |
Analogous to the two-part division of the foregoing table into biological function and factory part for different Organelles, binary code used in computers, the binomial taxonomic system used in biological classification, the dots and dashes of Morse code, the idea that atoms act like both waves and particles, life originated by the interaction of two pre-cell proto-organelles (endosymbiosis), and multiple other two part divisions which may be called dichotomies, dualities, oppositionals and the like. I mention this because a spate of two-part divisions are to be found as a basic formula in mathematics as well, and can remind one of the divisions found in the variety of yin and yang examples such as hot/cold, man/woman, east/west, etc... The need for highlighting the existence of such which is most often taken for granted by mathematicians, is that it can be identified as being reminiscent of a basic cognitive construct that is identified by psychologists and called Persistent Dichotomies. The persistent usage of such dichotomies has come under fire as being obsolete of in the fact that it is used as a model framework of primary value instead of as a general reference. This same goes for mathematics, except that much of mathematics is structured on dichotomies. There are so many that I have needed a separate webpage to catalog them along with examples of a few trichotomies.
The persistence of dichotomies in the study of behavioral development by Timothy D Johnston
Psychologically, interactionism refers to the theory that the mind is composed of two separate entities, mind and body, each of which affects the other. ... In sociology, interactionism becomes a theoretical perspective that tries to derives social processes from human interactions.
Sociologically, interactionism becomes a theoretical perspective that tries to derives social processes from human interactions. These processes (such as conflict, cooperation, or identity formation) are examined as a study of how individuals can shape their society and are likewise shaped by society.
Interactionism
With respect to Mathematics, Interactionism is persistently addressed in terms of methodology for teaching mathematics and not applied to mathematical equations, though polynomials are as much variables situated in the environment of a given equation as are students in a classroom.
However the foregoing link about the inadequacy of using Persistent Dichotomies finds itself supporting the notion of an interactionist approach with its attempt to convey a model involving multiple (more than just two) facets to explain behavior, yet the model itself becomes dressed into dichotomies such as from lower to higher, simple to complex, and like-minded alternatives; with the supposed reality of factuality to be obtain somewhere betwixt the extremes... thus producing a third component which can be mathematically represented by the simple equation if not A and not Z, then some value in between... where the value in between is used to defend the idea that it is not in a central position but other-than center yet nonetheless between the points of whatever dichotomy is in vogue. It honestly conveys (to me) an image very much like the creative mathematical methods of some accountants... particularly those who like to "fudge" numbers. Words and interpretations allow for a widespread means of supporting an interactionist view since multiple variables can be added, subtracted, multiplied or divided arbitrarily; unlike a standard math formula that abides strictly to the rules of production and manufacture to make sure the end product conforms to whichever cookie-cutter expectation is being used for a given moment.
Nonetheless, while the Interactionist model may find support amongst those in Psychology and Sociology, its value for the present discussion is meant to point out how dependent mathematics and other genres of study are persistently dependent on using dichotomies without the users even being aware of an underlying mathematical scenario is taking place in their active brain processing.
As a reader you may be saying: "So what?" "If it's that persistent, then it must be a natural law of human brain activity." The problem with this statement is that it does not reflect the supposed whole law, otherwise we would have a doublet code in DNA instead of a triplet one and atomic particles would occur in groups of two instead of three... since our consciousness would preferentially want to see things in groups of two instead of three if a supposed "Natural Law of Twoness" existed. There would be no need to have basic arithmetic because the basic processes of addition, subtraction, multiplication and division all seek to convey a third item from the interaction of at least two numbers... or variables.
A comment taken-out-of-context regarding production lines and ergonomic issues, here is a reference that can be aligned with attempts to improve the quality of the finished product in order to reduce the possibility of variability arising; whereby once proofed, a math statement can assert itself as a constant... and yet, how do we proof a proof or proofing process when this describes the existence of a possible problem, yet there is an unspoken acceptance that the effort to use a proofing methodology excuses oneself from a situation which echoes the old religious idea of infallibility? In other words, so long as one asserts they are at least trying to engage in a presumed proofing process, they can thus escape from being viewed as engaging in some gamesmanship of stacking the deck (so-to-speak) in favor of their mathematical expressions? Using the word "proof" has gained such a status of fame and desired unblemishable honesty, it is accepted without question as "THE" ways-and-means for dispelling contrary revelations which would signal and inconstancy, just like many people do when one speaks of a god, religious leader, or some admired authority figure. However, we can at the very least provide a measure of deference to attempts by 'proofers' regarding their sincerity when they quite often and unapologetically... without reservation, reveal that there are common mistakes being repeated in the proofing process. In terms of a production line, the proofing process is synonymous with quality control for the purposes of quality assurance guided by quality management.
A Primer on Mathematical Proof (Common Mistakes in Proof-Writing):
- Starting with the conclusion, and working backwards toward the hypotheses.
- Checking the conclusion in a few specific examples, and extrapolating that it always holds.
- Assuming the conclusion.
- Making steps in the proof without adequate justification.
- Overlooking special cases.
- Undeclared variables and undefined notation.
- Imprecise statements.
- General bad communication.
And let me add another item in which all of Mathematics has embraced a system of thinking where the word "Proof" accurately and honestly describes a desire to prove correctness or appropriateness in a standardized way, when some equations require a different methodology of proofing that, fore the most part, is not even on the radar of many mathematicians to consider.
In questioning the proofing process as proof enough just because one uses the word "proof" to describe a process that may be inherently flawed but can not be seen as such because everyone excepts— it since it carries the inviolable label of "proof" as its own proof of being certain... is tantamount to the idea that a person accused of witchcraft can be tested by dunking them in a body of water. This type of "proof" testing is accepted as a valid process, and even if one disagrees, they remain silent about it an will voice a belief in witches and witchcraft or demons, dragons, etc., so as to remain being seen as "one of the group" who is entitled to share in the rewards dispensed by those whose authoritative judgment determines what is and what is not to be believed. If the accuses drown, they can be claimed as innocent, and if they don't drown by the adopted currency of time allotted to leave one under the water; then they must be guilty and therefore need to be subjected to a more lengthy examination requiring a different model of extended computation to ensure that the person's guilt and innocence are given "their day in court" (so to speak), even if the case against them is most assuredly going to end in a guilty verdict so as to maintain the public faith in current standards of observance and practice. Periodic sacrifices and/or bloodletting are powerful stimulants for swaying opinions in a given direction... even though history frequently speaks of those whose ideas were later to be found correct.
...In striving for improved product quality, approaches have traditionally emphasized design of product and process to reduce variability...
Ergonomics of Assembly Lines by Ben Michael BNP61, April 26, 2018
Looking at Mathematics as a multi-step manufacturing process that might be viewed as a type of Ppolynomial expression:
- Product concept (raw materials: assumptions, beliefs)
- Processing/manufacturing (raw materials subjected to equations: add this, subtract that, multiply this, divide that)
- Product generating (result viewed as tentative truth)
- Proofing (quality control where product is subjected to this, that and the other questions as defensible, definitive or dismissing the negligible)
- Perception (accepted proof established as reality)
However, the once hand-operated grist mill was then altered into a mechanized draft animal mill, out of which came a mechanical model that has now become an electro-mechanically designed compilation that is assisted in its operation by computers whose language is upgraded, downgraded, or equalibriated because the underlying operations language has become intoxicated that frequently produces situations reminiscent of the Tower of Babel idea.
 |
 |
 |
 |
 |
| |
| |
My perception of current mathematical equations persist in revealing an illustration that does not speak of a cryptic foreign language, but an ideographic architecture of neolithic art commensurate with the idea of picture rocks or pictographs. Similarly, we don't see movement in such expressions without projecting movement onto the images. Otherwise, like equations, they are static. They do not breathe as one might imagine an Accordian breathing in and out in order to produce a message. The currency of messages being fostered (and handed out like some social security benefit) taking place both in an out of mathematics, concerns whether mathematics is:
- a separate (stand alone) language.
- a supplemental (to typical speech-articulated) language,
- a separate language supplemented by crude (primitive) hand gestures, facial/body language and symbolic references, striving to emerge from its stage of development still in a cacoon.
To the last item, it should be clarified that there are those who think mathematics has not yet come unto its own as a fully mature entity waiting to be birthed from its present still-in-the-womb/cacoon developmental stage of potentiality, and that even current mathematics expressions, however labeled, are themselves restraining further development; thus calling for a revision of the present mathematical ideal. In any respect, whatever clarion call appeals to you, many are inclined to accept mathematics as representing some level of expressed language that is striving to be THE foremost language that everyone in the world should accept as the Linga-Franca of humanity. And by such an acceptance, a greater truth and harmony will emerge because all misunderstanding and ambiguity will be removed from interpretation and communication.
By adopting a pure form of mathematics, as it is said by adopting the ONE true religion, or one true political philosophy, or the one true form of music, or one true form of ecology, economics, dietary regime, day-to-day living routine of moderation, etc., all of humanity can prosper to the point of achieving its greater potentiality. Mathematicians claim that all things are basically number, geometry and algebra either separate or combined commodities there of. Likewise, their are those who believe if everyone adopted their One True religion, the whole of humanity would be the better for it, because all things are basically religion aligned with a ONE TRUE god... even mathematics. Then again, some say that all things can be reduced to music, including religion and mathematics, such as expressed in the old expression "music of the spheres". Others say that everything can be broken down into chemistry, or physics, or biology, or some asserted metaphysical criteria where there is supposed to be no upmanship in ideas to be furthered. In other words, what a mess humanity has made of genuinely honest perceptions. All the ideas are like the community of citizens who are required to overlook the nudity of the King parading throughout the public, and to silence those who practice a rather astonishingly simple perspective described as being "out of the mouths of babes." Indeed, all the subjects concocted by humanity are like the King whose supporters insist that everyone overlook the raw facts and agree with the stated illusions to the point of creating inter-generational delusions.
However, before proceeding with the present philosophical sojourn, let me back up a bit to give you the run down on how I came about to think in such a manner as is being expressed with multiple digressions being used as metaphorical and analogical representations.
I was laying down in the early evening (last night, the 25th of February, 2021) intending to try and fall asleep, but the churning of my mind occasioned for me to grab for a paperback desk encyclopedia to look up the word Gravity (pages 529-530). While I had been thumbing through it (like someone does a magazine in a doctor's office awaiting their turn to be called into a backroom to be examined) before laying down, different ideas were mulling around as one might encounter as they peruse events they experienced in the day or some supposed future event which might occur. If I didn't grab a book or work on some project, my thoughts can go every which way without much direction unless something grabs my attention and I focus on it. It's like a person who is addicted to caffeine or alcohol or music or something else, and need to "calm their nerves" by ingesting a small portion of some substance to effect a type of tonic or bandaid on an experience that would otherwise throb-about their attention much like a dripping faucet. My substance to direct the focus of my otherwise divergent conceptualizations was to read the description about gravity which was absent, but the word "gravitation" did exist along with an equation which I replayed over and over again in my mind.
The passage accompanying the equation reads as this: Newton's law of universal gravitation states that the attractive force F between two bodies of masses M1 and M2 separated by a distance d is The equation was in the standard form of: F = GM1M2/d2 where G is the Universal Gravitational Constant (6.670 X 10-11 NM2 kg-2.

Newton's Cradle
The rest of the article reads as this: The force of gravity on Earth is a special case of all attraction between masses and causes bodies to fall toward the center of the Earth with a uniform acceleration g = GM/R2 where R and M are the radius and mass of the Earth. Assuming, with Newton, that the inertial mass of a body (that which is operative in the laws of motion) is identical with its gravitational mass, application of the second law of motion gives the weight of a body of mass m, the force with which the Earth attracts that body, as mg. Bodies on the Earth and Moon may have the same mass but different weights. Again, the gravitational force on a body is proportional to its mass but is independent of the type of material it is. Newton's theory explains most of the motions of the planets and the tides and is still sufficiently accurate for most applications. The Newtonian analysis of gravitation remained unchallenged until, in the early 20th century, Einstein introduced radically new concepts in his theory of general relativity. According to this, mass deforms the geometrical properties of the space around it. Einstein reaffirmed Newton's assumption regarding the equivalence of gravitational and inertial mass, proposing that it was impossible to distinguish experimentally between an accelerated coordinate system and a gravitational field. From this he predicted that light would be deflected a certain amount toward massive bodies by their gravitational fields and this effect indeed was observed for starlight passing close to the Sun. It was also predicted that accelerated matter should emit gravitational waves with the velocity of light, yet the existence of these as not as yet been demonstrated.
The desktop encyclopedia in use has the last copyright date of 1989. Some of the material is rather dated. However, my thoughts created an image of the equation juxtaposed with separate images of each variable. In hindsight, though I did not voice this perspective at the time, I realized that the equation was static. It did not express "movement" as a keyword used to describe Calculus, instead, the equation, to me, was expressing a static position or moment...not movement:
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations.
Statics is the branch of mechanics that is concerned with the analysis of loads (force and torque, or "moment") acting on physical systems that do not experience an acceleration (a=0), but rather, are in static equilibrium with their environment.
The equation was static, that is, non-moving in the usage of its given variables. Movement occurred by way of assumptions being projected on to the elements of the equation by the person viewing it. In other words, it did not give a description of movement because it lacked a description of some needed expressions (let me itemize):
- Force with variability
- Gravity with fluctuation
- Mass with different types and quantities (as well as positive and negative variations)
- distance which portrayed a proportional relevance to relativity
- Force is measured in Newtons
- Mass is measured in kilograms squared over meters squared, yet, since newtons and kilograms are not equivalent, we use...
- Gravity measured as meters squared over kilograms squared times newtons... or taken directly from the horse's mouth so-to-speak:

Gravitational Constant Explained
Let's face it with a bit of honesty. Using axioms derived from beliefs and assumptions can be a hit and miss proposition. However, though we recognized the very real presence of beliefs and assumptions under-girding mathematical forays, we buttress our attempts for justification and validity by claiming that the component processes of computation makes the overall usage of mathematics a formal exercise of credibility. Hence, let me use a reference from one of Gulliver's Travels journal, as a metaphor underpinning the current mathematical equation situation:

The argument goes that mathematics is computation and that this is not a belief or assumption, even though the computation arises from axioms and beliefs. In other words, do we accept the position of our beliefs corresponding to breaking the egg at the little end or come to agree with our assumptions corresponding to breaking the egg at the big end (unless you prefer the roles reversed) with computation taking a central "centered" position and add a bit of humor by saying that you can't make an omelet without breaking a few eggs, or that a person is a "good egg" if they go along with a given agreement? However, if one thinks the analogy in poor taste because they don't like eggs or have a beef against the eating of animals, then the Blind Men and Elephant poem may be your cup of tea with a danish.
Date of Origination: 26 February 2021... 6:59 AM
Initial Posting: June 4th, 2021... 7:06 AM