Religion, Mythology, Metaphysics
(The Study of Threes)
http://threesology.org
| In The Beginning page 1 |
In The Beginning page 2 |
In The Beginning page 3 |
In The Beginning page 4 |
In The Beginning page 5 |
In The Beginning page 6 |
In The Beginning page 7 |
Since different readers may come to one of the pages in this series other than the first page, it is necessary that the following paragraph be placed on all of the pages:
In The Beginning... that is, after the development of biology and the semblance of culture after the early hominids and initial emergence of what we of today denote as modern man designated by Cro-Magnons. And yet, "the beginning" is not limited solely to western perspectives of early religious thought and later ideological correlations. And though we of today describe many of the early ideas as myth and legend, those in the past may well have viewed such ideas as being factual. Yet, the point to be made in the present series of "threes" examples is that there was and is a current of thought processing which regularly used patterns-of-three to organize information... or at least we of today use patterns-of-three even if peoples in the past had no particular affection for one or another numerological pattern before or after Pythagoras' formula of "numerology"... and is a word conjuring up the ideas of magic, mystery and mysticism... which is closely related to many religious preoccupations involving "non-rational" (or mere philosophical) themes...
... Hence, the role of "numbers" (however one may interpret this abstract conceptualization), plays a large role in theological scriptures and conversation. Had Euclid's ideas preceded Pythagoras, the religions of today might be quite different, because his way of thinking signaled a change in the human brain, and may in fact describe a different type of human species— though we may still ascribe them to the overall Hominoidea characterization that appears to comprise the words "Homonoid" and "idea" (referring to Anthropoid apes and human beings). Indeed, the rise of mathematical thinking attests to the notion that there was a change not only in human thinking, but perhaps the human brain itself... which is not limited to the subject of mathematics as an indicator, and suggests that many of the so-called human social problems being encountered is due to the presence of more than one type of human-like species trying to co-exist.) A short digression into number theory is therefore appropriate at this point as a means of pointing out differences in thinking patterns suggestive of differences in human brain function respective of evolutionary changes coupled to a incrementally deteriorating planetary system and Earth environment. (Note: the following Four Euclidean propositions said to deserve special mention can be viewed in a 3 to 1 ratio way, such that the first three can be differentiated from the one— or fourth example:)
(Number Theory) From prehistory through Classical Greece The ability to count dates back to prehistoric times. This is evident from archaeological artifacts, such as a 10,000-year-old bone from the Congo region of Africa with tally marks scratched upon it—signs of an unknown ancestor counting something. Very near the dawn of civilization, people had grasped the idea of "multiplicity" and thereby had taken the first steps toward a study of numbers. It is certain that an understanding of numbers existed in ancient Mesopotamia, Egypt, China, and India, for tablets, papyri, and temple carvings from these early cultures have survived. A Babylonian tablet known as Plimpton 322 (c. 1700 BC) is a case in point. In modern notation, it displays number triples x, y, and z with the property that x2 + y2 = z2. One such triple is 2,291, 2,700, and 3,541, where 2,2912 + 2,7002 = 3,5412. This certainly reveals a degree of number theoretic sophistication in ancient Babylon. Despite such isolated results, a general theory of numbers was nonexistent. For this—as with so much of theoretical mathematics‐one must look to the Classical Greeks, whose groundbreaking achievements displayed an odd fusion of the mystical tendencies of the Pythagoreans and the severe logic of Euclid's Elements (c. 300 BC). |
Pythagoras According to tradition, Pythagoras (c. 580–500 BC) worked in southern Italy amid devoted followers. His philosophy enshrined number as the unifying concept necessary for understanding everything from planetary motion to musical harmony. Given this viewpoint, it is not surprising that the Pythagoreans attributed quasi-rational properties to certain numbers. For instance, they attached significance to perfect numbers—i.e., those that equal the sum of their proper divisors. Examples are 6 (whose proper divisors 1, 2, and 3 sum to 6) and 28 (1 + 2 + 4 + 7 + 14). The Greek philosopher Nicomachus of Gerasa (flourished c. AD 100), writing centuries after Pythagoras but clearly in his philosophical debt, stated that perfect numbers represented "virtues, wealth, moderation, propriety, and beauty." (Some modern writers label such nonsense numerical theology.) In a similar vein, the Greeks called a pair of integers amicable ("friendly") if each was the sum of the proper divisors of the other. They knew only a single amicable pair: 220 and 284. One can easily check that the sum of the proper divisors of 284 is 1 + 2 + 4 + 71 + 142 = 220 and the sum of the proper divisors of 220 is 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284. For those prone to number mysticism, such a phenomenon must have seemed like magic. |
Euclid By contrast, Euclid presented number theory without the flourishes. He began Book VII of his Elements by defining a number as "a multitude composed of units." The plural here excluded 1; for Euclid, 2 was the smallest "number." He later defined a prime as a number "measured by a unit alone" (i.e., whose only proper divisor is 1), a composite as a number that is not prime, and a perfect number as one that equals the sum of its "parts" (i.e., its proper divisors). From there, Euclid proved a sequence of theorems that marks the beginning of number theory as a mathematical (as opposed to a numerological) enterprise. Four Euclidean propositions deserve special mention. The first, Proposition 2 of Book VII, is a procedure for finding the greatest common divisor of two whole numbers. This fundamental result is now called the Euclidean algorithm in his honour. Second, Euclid gave a version of what is known as the unique factorization theorem or the fundamental theorem of arithmetic. This says that any whole number can be factored into the product of primes in one and only one way. For example, 1,960 = 2 × 2 × 2 × 5 × 7 × 7 is a decomposition into prime factors, and no other such decomposition exists. Euclid's discussion of unique factorization is not satisfactory by modern standards, but its essence can be found in Proposition 32 of Book VII and Proposition 14 of Book IX. Third, Euclid showed that no finite collection of primes contains them all. His argument, Proposition 20 of Book IX, remains one of the most elegant proofs in all of mathematics. Beginning with any finite collection of primes—say, a, b, c, ..., n—Euclid considered the number formed by adding one to their product: N = (abc···n) + 1. He then examined the two alternatives: (1) If N is prime, then it is a new prime not among a, b, c, ..., n because it is larger than all of these. For example, if the original primes were 2, 3, and 7, then N = (2 × 3 × 7) + 1 = 43 is a larger prime. (2) Alternately, if N is composite, it must have a prime factor which, as Euclid demonstrated, cannot be one of the originals. To illustrate, begin with primes 2, 7, and 11, so that N = (2 × 7 × 11) + 1 = 155. This is composite, but its prime factors 5 and 31 do not appear among the originals. Either way, a finite set of primes can always be augmented. It follows, by this beautiful piece of logic, that the collection of primes is infinite. Fourth, Euclid ended Book IX with a blockbuster: if the series 1 + 2 + 4 + 8 + ... + 2k sums to a prime, then the number N = 2k(1 + 2 + 4 + ... + 2k) must be perfect. For example, 1 + 2 + 4 = 7, a prime, so 4(1 + 2 + 4) = 28 is perfect. Euclid's "recipe" for perfect numbers was a most impressive achievement for its day. |
Diophantus Of later Greek mathematicians, especially noteworthy is Diophantus of Alexandria (flourished c. 250), author of Arithmetica. This book features a host of problems, the most significant of which have come to be called Diophantine equations. These are equations whose solutions must be whole numbers. For example, Diophantus asked for two numbers, one a square and the other a cube, such that the sum of their squares is itself a square. In modern symbols, he sought integers x, y, and z such that (x2)2 + (y3)2 = z2. It is easy to find real numbers satisfying this relationship (e.g., x = ∫2, y = 1, and z = ∫5), but the requirement that solutions be integers makes the problem more difficult. (One answer is x = 6, y = 3, and z = 45.) Diophantus's work strongly influenced later mathematics. |
Number theory in the East The millennium following the decline of Rome saw no significant European advances, but Chinese and Indian scholars were making their own contributions to the theory of numbers. Motivated by questions of astronomy and the calendar, the Chinese mathematician Sun Zi (Sun Tzu; flourished c. AD 250) tackled multiple Diophantine equations. As one example, he asked for a whole number that when divided by 3 leaves a remainder of 2, when divided by 5 leaves a remainder of 3, and when divided by 7 leaves a remainder of 2 (his answer: 23). Almost a thousand years later, Qin Jiushao (1202–61) gave a general procedure, now known as the Chinese remainder theorem, for solving problems of this sort. Meanwhile, Indian mathematicians were hard at work. In the 7th century Brahmagupta took up what is now (erroneously) called the Pell equation. He posed the challenge to find a perfect square that, when multiplied by 92 and increased by 1, yields another perfect square. That is, he sought whole numbers x and y such that 92x2 + 1 = y2—a Diophantine equation with quadratic terms. Brahmagupta suggested that anyone who could solve this problem within a year earned the right to be called a mathematician. His solution was x = 120 and y = 1,151. In addition, Indian scholars developed the so-called Hindu-Arabic numerals—the base-10 notation subsequently adopted by the world's mathematical and civil communities. Although more number representation than number theory, these numerals have prevailed due to their simplicity and ease of use. The Indians employed this system—including the zero—as early as AD 800. At about this time, the Islamic world became a mathematical powerhouse. Situated on trade routes between East and West, Islamic scholars absorbed the works of other civilizations and augmented these with homegrown achievements. For example, Thabit ibn Qurrah (active in Baghdad in the 9th century) returned to the Greek problem of amicable numbers and discovered a second pair: 17,296 and 18,416. Source: "number theory." Encyclopædia Britannica Ultimate Reference Suite, 2013. |
And inasmuch as we of today use enumeration to list multiple examples from not only different cultures regarding the same subject, we also include examples from a diverse array of subjects because all of them represent a collective human cognition. Providing numerous examples-of-three does not in any way suggest there are no other patterns nor that it is the sole dominant pattern in every instance. Clearly, because there are multiple number patterns but that the overall list of number patterns is small, suggests human cognition is either limited in its processing ability due to a genetic design, and/or that there is an external factor that is or was dominant in creating such a limitation on human physiology and overall genetics. In addition, if it is due to an environmental factor and that factor(s) is deteriorating (or otherwise), then it is prudent for us to take stock of such a situation as a means of prediction and possibly control.
In the beginning... there were none of the businesses, politics nor religions we have today. In fact, there were no humans, no other animals, insects, plants, aquatic life forms or the Earth itself, including the Universe as well. The three-patterned "In The Beginning" phrase is typically defined within a religious context that far too many people have come to accept as a truth akin to some universal law, but it shouldn't be. Religious ideas are just varying forms of philosophy. They typically are theories whose truth is based on belief substantiated by faith. Such theories are often developed and maintained by groups of people who share a similar frame of mind by defining personal experiences in terms of a "spiritual" framework. This is not to say that some religious ideas are not wholly or partially derived from some perceived actual event or that some actual historical event took place in the exact manner, the exact place or the exact people as is documented. Some beliefs are made up and are thus truly fictional. Some are bits and pieces of a reality that memory may or may not recollect correctly. Other portions may be so accurate that the perception of common people, even those living today, would have difficulty in grasping the reality of occurrence without resorting to some level of personalized alteration of events for which they can best describe within their individual abilities, good or bad.
This framework is what most, but not all religious-minded individuals interpret to be factual evidence for the existence not only of one or more gods, but that the entire scope of their religious doctrine is valid. In short, they want to believe in religious ideas and very often interpret experiences (theirs and others) within the context of some religious notion. To not believe in some religious doctrine fills them with fear that a god will somehow retaliate against them, or that they will be abandoned (like a child) to all the evils of the world, including the epitome of human evil called Satan, the Devil or the Anti-Christ. Some even fear they will have to spend an inordinate amount of time and energy defending themselves from those who will call them an atheist.
First of all, the word "atheist" is frequently misused, misapplied and misunderstood. For some, it is used strictly to define someone who doesn't believe in one or more gods. A few use it to define a disbelief in the one or more religious doctrines or some specific religious belief. And some use it to define a belief in God but a disbelief in their experiences with religion. Atheism has thus evolved into its own three brands of dominant "religiosity". Many of its adherents are just as tunnel-visioned as those advocating some religious precept.
Let us make a couple of general comments regarding religious and atheist believers:
- On the one hand, there are those who believe in some religious doctrine that think it their God-directed purpose to preach the "gospel" (their presumed truth), and rid the world of evil (as they perceive it through personalized definitions) in order to get everyone to travel the right path, which commonly means away from disbelieving in what they believe.
- There are those who define themselves (in one way or another) as an atheist, who think it their life's purpose and right to dispel the presumed evils being espoused by those advocating one or another religious doctrine.
- Some observers tend to define themselves (whether verbally or just mentally), as being opened minded, yet in their attempts to be broad thinkers, they too ultimately choose what is or is not atheism or religion.
Those advocating a religious perspective typically define most things, if not everything in some instances, within a religious context. This has nothing to do with morality and immorality. Morality and immorality are terms that religious oriented people attempt to claim belong to them, thereby permitting them to define such terms within the specifics of a religious belief. But not only do religious doctrines attempt to claim ownership to many different ideas, so does science, and law, as well as criminality. The criminal interprets reality in the way they think, which very often is illegal. Yet, because our laws have particular definitions in different contexts, those who don't break civil laws are considered, for the most part, to be law-abiding citizens.
All professions breed some level of tunnel-vision perspective. But most of us come to realize this and accept it as an indication of our human limitations. Whereas we come to acknowledge the existence of human limitations, not only in physical but mental activity, some have ventured to include that human spirituality is likewise limited. With this said, many of us would, upon careful reflection, agree with this assessment of humans. But such an acceptance leads some of us towards examining human physiology, our mentality, and the presumed separate and distinct spirituality from the perspective of cataloguing commonalities (which include common differences), amongst the many beliefs, be they religious, economic, political, scientific, etc...
Many researchers come to identify universal laws in their respective field of interest. As a Threesologist (though you may prefer to use the title of Triadologist, or some similar denotation of a threes researcher), I like to look at not only the research findings of all the researchers, regardless of their interest, but also the commonalities of common perspectives and behaviors. Thus, when I encounter the expression "In The Beginning," it is interpreted in the context of threes research as a pattern-of-three, and not as a religious expression. The same goes for such "religious" notions as Father- Son- Holy Ghost/Spirit. It too is a pattern-of-three. To this we could add Brahma- Vishnu- Siva and the 666 as being (religiously) represented as a (number code) sign of the Devil, or 888 as a "code" for Jesus.
Threes research using examples from religion is not about advocating a particular religious doctrine. Likewise, a phrase such as "I Am God" used in another section as an exploration of the God concept, is not about representing a philosophical stance for or against God, regardless of your religion. Some might consider it to be a new religion in the making, but that is their interpretation. Even those who write original ideas or paint original perspectives, may not have a comprehensive grasp of how wide-ranging an effect their efforts may have in the present or future.
The title of this page begins the section on threes research into as many religions as I can find, will no doubt embody years of research by more than just myself. It should necessarily include pseudo- or wannabe (want to be) a religion ideas as well. I don't care if they are ancient views defined in a modern setting as a pagan religion. I don't care if during the time of belief the ideas were considered science, magic, mythology, or something else, good or bad. It doesn't matter. If you feel that one or another example should be placed into a different context, make up your own list or let me know and I will make up a page with what you think is appropriate to be considered. Granted, there will have to be an accountability with respect to overall context in which items should be catalogued. Certain catalogs provide more useful information than do other arrangements. Inevitably, different catalog arrangements will be made by those who identify other characteristic commonalities that are not being addressed by the simplistic manner in which current threes lists are being arranged. Nonetheless, let me begin with my examples that you may or may not define as religion, mythology or metaphysics...
Late 19th and early 20th century Anthropologists searched for the historical origins of religion and tended towards a tripartite, quasi-evolutionary progression from: |
3 great Monotheistic religions: Islamic~ Judaic~ Christian
3 different ways of spelling an ancient Egyptian deity:
1. Amon (â´men, ä´-)
2. Ammon (à´men)
3. Amen (ä´mèn)
Originally the chief god of Thebes, Amon grew increasingly important in Egypt, and eventually, as Amon Ra (Ra = Solar god), he was identified with RA as the supreme deity. He was also identified with the Greek ZEUS (the Roman JUPITER... 'Zues-Pater'... 'Zeus our father'). (Jesus = JeZeus)
Note: the present-day usage of the word "amen" to signify the closing of a prayer is yet another representative clue that modern religions have historical connections to ancient solar worship. We could also include the three-letter meditation (chant) word AUM (Om) as a derivative of the A...u- men Ra reference.
Amen-Ra was one third of the Great Triad of Waset along with Mut and Khensu who were the other two thirds.
Amen-Ra was a dual deity devised to merge the worship of Amen with the older solar cult of Ra. By combining the two, the deities are said to dwell within one another.
http://www.uponreflection.co.uk/heiro/gods/amen_ra.htm
| 3 physical "points" to the devil: 1 = tail 2 = horns 3 = canines 3 to 1 ratio of points to the devil: 3 prongs to 1 pitchfork. 3 physical distinctions of a satyr in Greek mythology: 1. Pointed ears 2. Pointed horns on the forehead 3. Pointed tail. 3 "H"-related attributes of the devil: 1. Hooves 2. Horns 3. Hell |
 --- Index of Image Archive --- |
 Om, in Hinduism and other religions chiefly of India, a sacred syllable that is considered to be the greatest
of all the mantras, or sacred formulas. The symbol Om is composed of the three sounds A-U-M (in Sanskrit, the vowels A and U coalesce to become
O), which are said to represent several important triads:
Om, in Hinduism and other religions chiefly of India, a sacred syllable that is considered to be the greatest
of all the mantras, or sacred formulas. The symbol Om is composed of the three sounds A-U-M (in Sanskrit, the vowels A and U coalesce to become
O), which are said to represent several important triads: 3 major Hindu gods: Brahma~ Vishnu~
Siva
3 major Hindu gods: Brahma~ Vishnu~
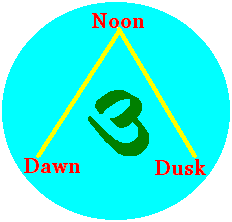
Siva3 sacred vedic scriptures: Rg~ Yajur~ Sama 3 powers: Action~ Knowledge~ Will 3 time periods: Dawn~ Noonday~ Dusk 3 manifested states: Gross~ Shapeless~ Subtle 3 elements: Fire (agni)~ Sun (aditya)~ Wind (vayu) 3 states of being: A. Wakefulness (jagaritsa-sthanta, corresponding to Vaishvanara). B. Dream (svapna-sthana, corresponding to Taijasa). C. Deep Sleep (sushupta-sthana, corresponding to Prajna). 3 worlds: Earth (Bhu)~ Heaven (Svar)~ Atmosphere (Bhuvas) 3 modalities or guna: Expansive (rajas)~ Cohesive or Ascendant (sattva)~ Destructive or Descendant (tamas) etc... thus: Om mystically embodies the essence of the entire universe. |
| Om is uttered at the beginning
and end of Hindu Prayers~ Chants~ Meditations, and is freely used in
Buddhist and Jaina ritual also. From the 6th century, the written
symbol designating the sound is used to mark the beginning of a text in a
manuscript or an inscription. The syllable is discussed in a number of the upanishads, which are the texts of philosophical speculation, and it forms the entire subject matter of one, the Mandukya. It is used in the practice of yoga and is related to techniques of auditory meditation. In the puranas the syllable is put to sectarian use; pranksthus the saiva mark the lingam, or sign of Siva, with the symbol for Om, whereas the vaishnava identify the three sounds as referring to a trinity composed of Vishnu, his wife Sri, and the Worshipper. |
***OM is linguistically represented in such words as omnipresent, omnipotent, omniscient, Amen (ahh-m--en), omnivorous, omnibus, omega (as in Alpha and Omega) etc., and perhaps even ominous, omelet, and the 17th & 18th century European card game called ombré.
If we view the "3" symbol of Om as symbolically representative of an environmental circumstance which:
- Was impressed upon the brow (physiology/genetics?) of humanity over centuries of exposure to it.
- That many people face East (rising Sun?) while in prayer.
- That mental symbols are mere metaphorical caricatures of such impressions...
...then the following image may be illustrative:
...the above image reflects "moments" in 1 Sun, which may have been the single most influential impression that encouraged humanity into developing a symbolic representation of early solar worship by adopting the idea of 3 "persons" in one God. Clearly, the Sun had been viewed as a God by early peoples and that this notion of solar worship is still practiced in Islamic traditions by an insistence of followers of praying towards the East, where the Sun rises.
| A question that needs to be asked at this point is whether the
significance of the "Three" idea expressed in the Celtic traditions
is: (1) Due to a Hindu influence. (2) Due to an as yet undiscovered non-Hindu influence. (3) Is an original conception based upon an evolving consciousness. or... the Celtic ideas influenced the Hindu (and other) "3"-focused traditions. |
It is important to observe that in the Middle Ages there was a Christian equivalent which was commonly used as a symbol of the "WORD."Glum This was the Siglum which was quite wrongly compared with the words 'Ave Maria'. In fact, this Siglum, pronounced in Latin with a sound similar to the Sanskrit AUM, meant "Alpha & Omega," 'the beginning and the end' (Revelation 21:6), and hence the evolution and involution of the cycle of manifestation. The Siglum gains added significance by its frequent association in medieval iconography with the Swastika, an emblem of the cyclical evolution of manifestation expanding from its immovable primeval center.
***It has been indicated that the neophyte of the Ephesian mysteries had to grasp the meaning of the "logos" (Word), that this world-creating Word revealed itself concretely through its 3-fold intonation of the vowels: I~ O~ A, vowels which were the subject of meditation.
Initial Posting (approx.): 29th March 2012... 9:42 AM
Updated Posting: 11th June 2018... 11:23 AM
Herb O. Buckland
herbobuckland@hotmail.com
