Dichotomies, Trichotomies, Quadrichotomies
Dichonions, Trichonions, Quaternions
twos, threes, fours
2s, 3s, 4s
Trichotomists as of July, 19th, 2025
Over the past 6+ decades, I have come across exposes' of ideas which directly or indirectly speak of patterns-of-two, patterns-of-three, and patterns-of-four. Sometimes they reference more than one of these three, at other times they reference other patterns. However, my interest at this moment is to focus on 2s, 3s, 4s as a particularized ensemble. Under the present circumstances, I was prompted to exercise a short essay in regards to Jessie Duffield's Stop Selling Me Trichotomies!, which speaks of various threes but his ending remark details a primary orientation: "If you can think of a fundamental trichotomy which is not composed of dichotomies, let me know!". His paper wonderfully displays an acknowledgement of twos, threes, and fours. In Addition, his dichotomy of "Fundamental/"Arbitrary" for deciphering the value of trichotomies is rather problematic: For example, when he lists his requirements for a Trichotomy, neither the triplet code of DNA/RNA, or the 3 germ layers, or the Neutron-Proton-Electron ensembles qualify:
- Each part is mutually exclusive, so no overlap.
- The whole is collectively exhaustive i.e. there's no missing parts.
- The division is globally true (not just in one specific case).
- It doesn't slice up a continuum.
He further states: "If you can't satisfy all those criteria, I will declare your trichotomy as arbitrary. Otherwise, I'll consider it fundamental."
Clearly the assumed universality of DNA's triplet code is not to be viewed as Fundamental, but an arbitrary concoction since multiple people have thought life to be the result of a fluke, an accident, a serendipitous event. Likewise Earth as the 3rd planet upon which the accident took place also is an accidental "chance" occurrence.
If we now compare the above list of qualifications to Euclid's Axioms, we see some similarities, but that both suffer from a limited range of knowledge and imposed limitations concerning their respective subject matters at hand:
- Things which are equal to the same thing are also equal to one another.
- If equals be added to equals, the wholes are equal.
- If equals be subtracted from equals, the remainders are equal.
- Things which coincide with one another are equal to one another.
- The whole is greater than the part.
Euclid's postulates exhibit the limitation to which his axioms were intended to be applied:
- To draw a straight line from any point to any point.
- To produce a finite straight line continuously in a straight line.
- To describe a circle with any center and distance.
- That all right angles are equal to one another.
- That if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the straight lines, if produced indefinitely, will meet on that side on which the angles are less that two right angles.*
As an example of Euclid's Axiomatic shortfalls, the internet AI provided the following response to the query "short falls of Euclid's Axioms":
Euclid's Elements, though foundational for geometry for centuries, had certain shortcomings that later mathematicians identified and addressed:
- Reliance on intuition and diagrams: Euclid's proofs sometimes relied on visual intuition from diagrams, rather than strictly on axioms and logical deduction. For example, in the very first theorem of his Elements, he assumes that two circles intersect, which should ideally be proven from the axioms.
- Implicit assumptions: Euclid made some assumptions that were not explicitly stated as axioms or postulates. These include:
- The concept of betweenness, needed for defining the inside and outside of figures.
- The assumption that points, lines, and circles exist and behave in ways consistent with their visual representation.
- A lack of a formal concept of continuity, which is necessary to prove the existence of certain constructed points and lines.
These "shortfalls" do not diminish the immense importance of Euclid's work, which established the axiomatic method as a cornerstone of mathematics. They prompted later mathematicians, notably David Hilbert, to develop more rigorous and complete axiomatic systems for geometry, making explicit all the necessary assumptions.
Similarly, the shortfalls of Jessie Duffield's "Axioms" of Trichotomy does not diminish the historic role in which they will play in the development of Trichotomization studies. He stands apart from others who have written about the "three" in his effort to establish some criteria for evaluating different expressions and usage of "threes" in terms of those examples which can be consider stable... and those that are temporary or faddish. However, the larger picture of a possible impermanence for humanity and perhaps all life suggests all examples are simply degrees of arbitrariness which human ego may selectively choose to label as being fundamental.
The problem begins with our initial assumptions long ago:
- We assumed that a point, and line are the most fundamental, most true objects of perception.
- We assumed the initial two objects were part of a wholistic set.
- We initially failed to acknowledge this set of two with the singular distinction of duality and complementarity.
- We initially failed to include space (called the "plane"), which became a later addition just as Astronomers initially failed to include the divisions of dark energy along with the darkness of space as being "matter" (later called dark matter) with observations of normal matter. (In some cases it was the plane and line that were first observed and the dot acknowledged later.)
- We failed to acknowledge that Europeans were using their own variation of duality to perceive and catalog reality, just as the ancient Chinese used the Yin/Yang model.
- We made the assumption to label a line and dot as Geometry, and then...
- to label Geometric figures with Numbers,
- and then to label the use of applied numbers as Mathematics,
- and then label Mathematics as a symbolic form of Geometry,
- and then assume contoured arrangements (algorithms) of Numbers to be a higher form of Geometry,
- and then view this "higher geometry" as a more fundamental and purer search for truth.
In International Morse Code, the space between a dot (dit) and a dash (dah) within the same character is equal to the duration of one dot. This means the "lag time" or gap between these two elements is a single unit of time, where a dot itself is defined as one unit of time. In short:
- Dot (dit): 1 unit of time.
- Dash (dah): 3 units of time.
- Intra-character space (between elements within a letter): 1 unit of time.
- Inter-character space (between letters in a word): 3 units of time.
- Word space (between words): 7 units of time.
By using the internet query "the most fundamental geometric figures", the AI rendered the following:
The most fundamental geometric figures are typically considered to be the point, line, and plane. These are the building blocks upon which all other geometric shapes are constructed.
- Point: A point has no dimension; it's simply a location in space. It's often represented by a dot.
- Line: A line is one-dimensional and extends infinitely in both directions. It's defined by two points.
- Plane: A plane is two-dimensional and extends infinitely in all directions. It's defined by three non-collinear points (points not on the same line).
- Circles: Defined by a set of points equidistant from a center point.
- Triangles: A polygon with three sides and three angles.
- Squares: A quadrilateral with four equal sides and four right angles.
- Rectangles: A quadrilateral with four right angles and opposite sides equal.
- The concept of a point is "No Thing" or nothing, that we can numerically reference in a simple way as zero... or even one.
- The concept of a line is the "1" (one)... or even two, when viewed as a stick with extended ends.
- The concept of a plane is the Many, the much, the all, the heap, the bunch, or even plurality.
- Number and Culture by Alexander I. Stepanov (speaks of triple structures, Quaternions [and other proportionalities in Politics, such as bipoloar party systems])
- Trinities In Everything by Erik Vertzvet (speaks of trinities and fours)
- The Law of Trichotomy, in its most common form for real numbers, states that for any two real numbers, x and y, exactly one of these statements is true: x < y, x = y, or x > y. This is a fundamental axiom in classical mathematics and forms the basis for ordering and comparing real numbers, integers, and rational numbers.
- However, the Law of Trichotomy is not universally considered true in all branches or interpretations of mathematics:
- Intuitionistic Logic: The Law of Trichotomy doesn't hold in general in intuitionistic logic. Intuitionism requires a constructive proof for the truth of a statement, and for some numbers or relations, it might not be possible to constructively prove which of the three conditions is true.
- Cardinal Numbers: In set theory (Zermelo-Fraenkel and Bernays), the Law of Trichotomy holds for the cardinal numbers of well-orderable sets. However, it doesn't necessarily hold for all cardinal numbers unless the Axiom of Choice is assumed (which allows all cardinal numbers to be well-orderable).
- Computer Floating-Point Arithmetic: While not a matter of formal mathematical truth, floating-point numbers in computers can have a "Not a Number" (NaN) state, which doesn't fit into the trichotomy of less than, equal to, or greater than.
- In conclusion, while the Law of Trichotomy is a foundational principle in classical real analysis and many areas of mathematics, its truth is conditional on the specific system of logic or number system being considered.
- Pair of shoes
- Pair of socks
- Pair of gloves
- Pair of (one) underwear (not pluralized)
- Pair of (eye) glasses
- Pair of (one) pants (pluralized)
- We don't say a pair of bras, hats, coats, or shirts or teeth.
- Common words:
- Pair: The most common word for two items of the same kind used together.
- Couple: Similar to pair, often used for two people or things joined together.
- Duo: A pair, especially of performers or musicians.
- Twosome: Two people or things together.
- Less common words
- Brace: Can refer to two items of the same kind, especially animals caught for hunting or fishing, according to Collins Dictionary.
- Dyad: A group of two people or things.
- Doublet: Historically, a pair of playing cards of the same rank. It can also refer to two similar or identical items.
- Couplet: A pair of lines in poetry, typically rhyming and of the same length.
- Span: In some contexts, a pair of animals (like oxen) working together.
- Twain: An archaic or literary term for two.
- Yoke: A pair of animals, especially oxen, harnessed together.
- Words derived from prefixes indicating "two":
- Bifurcation: The division of something into two branches or parts.
- Bilateral: Having two sides or relating to two sides.
- Bipartite: Consisting of two parts.
- Duplicity: Deceitfulness; a double-dealing attitude.
- Duality: The state of being twofold or having two parts.
- United States: 9 digits.
- France: 13 digits.
- Canada: 9 digits.
- Japan: 12 digits (My Number).
- Bahrain: 9 digit personal number.
- Pakistan: 13 digit identification number.
- Sri Lanka: 10 digit Unique National Identity number.
- Germany: 12 digits.
- Afghanistan: 3-digit national identification number.
- Bahrain: 9 digits (Personal Number, includes a check digit).
- Czech Republic: 10 digits (Birth number).
- Kazakhstan: 12 digits (Individual Identification Number for individuals, Business Identification Number for legal entities).
- Israel: 9 digits (Identity Number).
From these fundamental figures, we can derive other shapes like:
A review of basic geometry can be helpful for some readers:
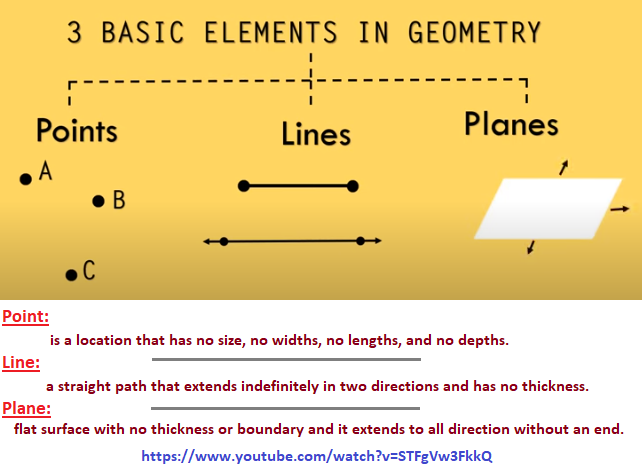
Note also that we can view the Geometric figures as enumeration, and hence, confronted by a basic model of the "One- Two- Many" early counting sequence:
Hence, the basic Geometric figures are easily aligned with basic quantitative variations primitive minds would have been confronted with while observing Nature without being subjected to all the present day forms of distraction.
In Jessie Duffield's theses which postulates an Axiomatic list of requirements for establishing a true Trichotomy, is itself an Arbitrary conjecture... albeit an honest attempt to formulate a premise upon which Trichotomists might establish a unified codification of characterization when dealing with triplicities. His efforts are noteworthy since they are pioneering, though incomplete... since he is starting from scratch and does not have the advantage of viewing other models of thinkers along these same lines... because they are virtually non-existent. Whereas he initiates the concept of ubiquity with the term "global", he does not reference this in terms of the 3 spatial dimensions nor time... even though "arbitrariness" suggests a time approximation and so does the use of the word "fundamental" in terms of appearance and longevity.
However, let me now digress and bring to the fore a mention of the other two articles for the present context and content:
The three foregoing papers on trichotomies show different positions with the additions of alternative views involving patterns-of -two and patterns-of-four. This reminds me of the Law of Trichotomy in Mathematics, which is thought to be false in some instances. There is no reason for it not to be false if one's underlying (basic) formulation is based on a persistence of dualities.
Here is the AI response to the query "is the law of trichotomies in mathematics considered to be false?":
A binary system is just as unstable as a bipedal gait without the use of a trimodal gyroscopic centering mechanism such as the inner ear's three semi-circular canals used for equalibrium.
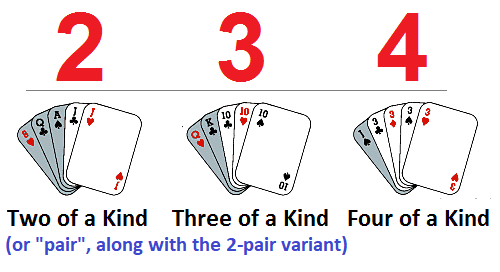
This page references triadic instances denoted as a 2-3-4 ensemble of information which occurs on two previous pages: Devil's Advocate 14A and B. Similarly stated, it entails making the acknowledged distinction for the presence of a triadic structure occurring with a "2-3-4" prominence such as for example the 2-of-a-kind, 3-of-a-kind, and 4-of-a-kind, with the "2-of-a-kind" generally noted as a pair, though the game of poker also provisions the "2" in a doubled format called two pairs. The preference for using "pair" or "two-pair" is not explained well by the internet's "AI". To claim it is redundant to say "two" when the use of the word "pair" is in common use doesn't explain why it isn't considered redundant to pair the similarity together. A better explanation is to say that the word "pair" for the quantity "2" has a longer history of usage and may be similar to the occasions in which we describe a quantity more then two as much, many, a few, a-lot, etc... However, if we look at the word "pair" in the context of clothing, we see the following:
If we include different synonyms for pair or two, we might use the following internet query "brace and other uncommon two-related words". And it is of interest to note the AI generated response didn't include the word "fork" as a fork in the road, and nor did it provide words such as dichotomy, binary, byad, binomial, duet, tandem, deuce, twin, etc., while many are specific to a topic and are not routinely used as general "2" references:
Several words relate to "two" or the concept of a pair...
While there are other types of Poker suits then the 3 enumerated ones, I am pointing out that only the 2-3-4 numerical values are described, even though "two-of-a-kind" is not "official" poker language:
Another example of enumerated tripartition is the U.S. styled Social Security Numbers. For example, 123-45-6789 exhibits a 3-part grouping arrangement of 3 numbers- 2 numbers- 4 numbers which is nine digits. Here are examples of counts for different models of Social Security/Identity/Health systems in the world, though I do not know the format in which the numbers are laid out in most circumstances:
Uses of numbers and letters combined to form a sequence for the purpose of establishing some semblance of a list, takes different, but very limited formulas. It is of value to understand what is and what is not be using by humanity to gain further insight into the present cognitive activity of humanity, typically being enforced by government-directed agencies. Human cognitive behavior with respect to an attachment to numbers exhibits a recurring compulsion to condense and symbolize, which relates to the need for survival under incrementally deteriorating planetary conditions.
Initial Posting:Saturday, July 12th, 2025... 3:33 AM
Updated Posting:Saturday, July 19th, 2025... 7:43 AM