(Basic Geometry of Cognitive Activity)
[1 point- 2 points- 3 points]
| RSP 1 | RSP 2 | RSP 3 | RSP 4 | RSP 5 | RSP 6 | RSP 7 |
Lookiloos as of August 4th, 2025
The origin of the rock-scissors-paper game is obscure. So too is the origin of geometry and counting. We of today simply make the best guesses we can. At one time, each in their own way, presented themselves as a revelation, if not revolution in thinking that one or more others may have been similarly excited about upon being told, or they were dismissive of it as just another crazy idea someone came up with. And even though Euclid (the Greek Mathematician) is considered by some to be the Father of Geometry, we don't really know if he originated all his mathematical ideas, or he "borrowed" them from someone else. Nor do we know how old the ideas of a point-line-plane actually are or where they came from. Mathematical ideas do not generally sprout out of some void where matter, dark matter, and dark energy intersect. Similarly, the same goes for the development of a counting system long before numbers were established or writing was invented.
It is likewise rather idiotic to think that the basic pattern of one idea is not being used in a different context with different words applied to some other subject. Hence, the 3-part concept of a point-line-plane could very well be a symbolic extension of the basic counting theme of 1-2-3, since this is the very quantity regularly used in basic geometry. In addition, the words and associated concepts of point-line-plane can also have parallel representations in other subjects if one does not lose sight of the fact that the human mind uses similar patterns of thought processing in different contexts, with different labels and adjustments thereof to fit the vernacular and particularized interests of those involved in a given practice. Hence, crosswords, puzzles, and the Rubik's cube have similar cognitive parallels. Yet, it is uncommon to find anyone searching for the origin and meaning of this behavioral repetition where patterns-of-three play a major role.
Whereas a rock, scissors and paper are items which can stand alone and be recognized individually, in the case of basic geometry and basic counting, an association with counterparts is required. In other words, the Point-Line-Plane of Geometry are a set, in as much as one might collect a set of small-medium-large items or label something slow-medium-fast, short-average-tall, lower-middle-upper, etc... Similarly, we associate numbers in some type as sequence as well. However, similar to the practice in chemistry that one molecule is not assigned a number value, this practice game about after the use of 2 and more molecules were identified. It was thought to be superfluous to place a "1" value next to a single molecule when the mere mention of a single molecule was its own obvious attribute. The absence of a number "1" for a single molecule can be viewed as the presence of a ghostly figure, an apparition, a shadow, or even echo.
The insightful beginnings of Geometry and numbers is...in effect, imaginative constructions of abstracted symbolism related to ghost, spirit, demon, monster, etc... tales originating... one might conjecture, in a very ancient time of superstition that was carried forward into the accepted and then normalized cults of civilization over vast ages of time and overlap, taking on the vernacular and garb of the respective contexts being practiced as ideologically constructed "mysteriums" that have become sustained cult beliefs themselves:
Internet query: "mysteriums of ancient civilization":
Throughout history, ancient civilizations have left behind artifacts, structures, and enigmatic records that continue to baffle researchers and fuel our imagination. Here are some prominent examples of unsolved mysteries associated with ancient civilizations:
- Lost cities and civilizations
- Atlantis: The legendary island kingdom described by Plato, according to Time Magazine. It's said to have possessed advanced technology and a powerful navy before being swallowed by the sea. Whether it was a real place or a philosophical allegory remains a topic of debate and speculation.
- The Lost City of Thonis-Heracleion: This ancient Egyptian port city, once a thriving trade center, was lost to the Mediterranean Sea around the 2nd century BCE, according to History.com. Rediscovered in the early 2000s, it's still unclear exactly why the city sank and how it remained so well-preserved underwater.
- The Indus Valley Civilization (Harappa): Flourishing around the Indus River, this civilization was highly advanced with well-planned cities and infrastructure, according to a user on Quora. However, the reasons for its abandonment around the 19th century BCE are still debated, with environmental factors like climate change and the drying up of the Saraswati River among the proposed explanations.
- The Minoan Civilization: Based on the island of Crete, the Minoan civilization was one of Europe's earliest advanced societies, according to a user on Quora. Their writing system, Linear A, remains undeciphered, hindering a full understanding of their culture, says a user on Quora.
- The Maya Collapse: Around 900 AD, the flourishing Maya civilization in Mesoamerica experienced a rapid decline, according to Live Science. While various factors like drought, deforestation, and warfare are considered, the precise reasons for this widespread collapse are still being researched.
- Megalithic structures
- Stonehenge: This iconic prehistoric monument in England is shrouded in mystery regarding its purpose and the methods used to construct it, according to WorldAtlas. Theories range from an astronomical observatory to a religious site or burial ground.
- The Nazca Lines: Enormous geoglyphs etched into the Peruvian desert by the Nazca culture between 500 BC and 500 AD, according to Ancient Origins. Visible only from the air, their purpose remains unknown, with proposed explanations including religious rituals, astronomical calendars, or communication with deities.
- Göbekli Tepe: Located in Turkey, this site is considered the world's oldest known temple, predating the development of agriculture, according to Live Science. Its purpose and the societal organization that allowed its construction by hunter-gatherers remain largely unexplained.
- Easter Island Moai: The iconic monolithic statues of Easter Island represent a significant mystery regarding their construction, transportation, and placement, as well as the reasons behind their eventual abandonment and the ecological collapse of the island's civilization.
- Lost technologies
- Greek Fire: A Byzantine incendiary weapon capable of burning even on water, according to Wikipedia. The exact composition and method of its creation are lost to history, according to a user on Quora.
- Damascus Steel: A type of steel used in the Middle East to forge incredibly strong and sharp blades, according to a user on Quora. The precise method of its production, involving Wootz steel from India, was lost after 1700 AD.
- Roman Concrete: Roman concrete was remarkably durable, and some structures built with it still stand today, according to a user on Quora. Its specific composition and the reasons for its superior longevity compared to modern concrete are not fully understood.
- Enigmatic artifacts
- The Voynich Manuscript: An illustrated codex written in an unknown writing system, according to Time Magazine. It remains undeciphered, with theories ranging from a hoax to a forgotten language or code.
- The Antikythera Mechanism: A complex astronomical calculator discovered in a Roman shipwreck, according to History Cooperative. This 2,000-year-old device demonstrates advanced mechanical engineering beyond what was thought possible for its time.
- The Copper Scroll: One of the Dead Sea Scrolls, it describes a vast treasure of gold and silver hidden throughout Judea, according to Live Science. However, the locations mentioned in the scroll are obscure, and the treasure has never been found.
- Cultural and ritualistic mysteries
- The purpose of Egyptian Pyramids: While generally believed to be tombs for pharaohs, the exact methods of their construction and potential other uses remain subjects of research and speculation.
- The Great Sphinx of Giza: The Sphinx's purpose, the identity of the pharaoh whose face it bears, and the possibility of chambers hidden beneath it continue to be debated.
- Rapa Nui (Easter Island) Culture: The reasons behind the creation and subsequent abandonment of the massive Moai statues, as well as the societal collapse on Easter Island, are still studied and pondered.
These examples represent just a fraction of the many intriguing mysteries left behind by ancient civilizations. With ongoing research and advancements in technology, some of these puzzles may eventually be solved, shedding more light on our past. Others, however, may forever remain shrouded in mystery.
The continued usage of basic geometry and basic enumeration can be viewed in terms of a basic cognitive patterning and function, but they are not. Much like the purported "real or true" message of Christmas having been adulterated by commercial interests, so too have the sustained interests in geometry and counting by the meddlesome business of education and its many instructors having become little different than door to door shysters and used car hucksters.
Thousands upon thousands of mathematic's instructors have no idea what the basic patterns of geometry and enumeration reveal about the repetition of human cognitive behavior and its parallels in different subjects representing a biological model of evolutionary development as a survival mechanism in response to an incrementally deteriorating planetary system.
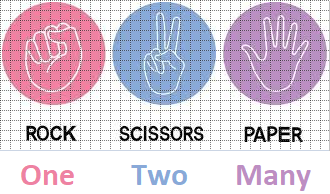
To understand the analogy being presented a bit better, it is of need to review the very basic assumption of geometry involving the three characters known as the Point-Line-Plane, and basic formative enumeration as it occurred in the distant past and referenced with the generality of "one- two- many", with or without number symbols. However, when permutations of parallel extensions are sighted in multiple other subjects, it should be understood that some concepts appear to be extensively orientated towards one or two aspects and leaving out the 3rd, though observers might misconstrue the volume of information being provided as a representative sampling of the three. For example, when speaking of basic elements (water, fire, earth, air, etc...) an observer may be distracted by some quantity exceeding the three columns, when in fact the information is just an elaboration of one of the columnar indices. Perhaps more simply put, a person might well elaborate on the point or the line or the plane column with a large amount of examples which causes the person to overlook the absence of the other two columnar figures and think that the quantity of the one column somehow satisfies the requirements of the other two.
- The Point is viewed as being non-existent (a "no-thing" without measure) but nonetheless given an identity by this gesture of reference. In other words, it is a ghostly figure.
- The line, if viewed as being infinite (in two directions... horizontal-vertical-or diagonal), has no measure of beginning or end or specialized distinction, unless at least one point is assigned to it... though it is typical that the value of "2" points is used.
- The Plane, if viewed as being infinite, typically receives 3 points in order to establish a coordinate identification.
Using the internet query "a plane with one, two, and three points", we get the following AI response:
In Euclidean geometry, three non-collinear points are always contained within a single, unique plane. A single point or two points can be contained in infinitely many planes. Here's why:
- One point: An infinite number of planes can pass through a single point.
- Two points: An infinite number of planes can pass through two points (a line).
- Three non-collinear points: Three points that don't all lie on the same line define a unique plane. Imagine stretching a sheet of paper to touch each of the three points; that sheet represents the unique plane.
- Four or more points: Four or more points are not necessarily coplanar (all on the same plane).
By using the query "a plane with one two, and three proints in non-Euclidean geometry", this is the AI response:
In Euclidean geometry, three non-collinear points uniquely define a plane. This means that if you have three points that do not all lie on the same straight line, there is only one possible plane that can contain all three. This is a fundamental concept in Euclidean geometry and is used to define planes in 2D and 3D spaces. Here's why:
- Two points define a line: In Euclidean space, any two points can be connected by a single straight line.
- A line and a point define a plane: A line and a point not on that line will define a unique plane.
- Three non-collinear points define a line and a point: Since the three points are not on the same line, any two of them will form a line, and the third point will not be on that line, thus defining a unique plane.
In non-Euclidean geometries, such as hyperbolic or elliptic geometry, the concept of a plane and how it's defined by points can be different. For example, in some non-Euclidean geometries, three points might not define a unique plane, or the concept of a "plane" itself might be different.
The Assumptions or Postulates of the basic trio of Geometry can be reviewed as:
- The Point is viewed as being non-existent (a "no-thing" without measure) but nonetheless given an identity by this gesture of reference. In other words, it is a ghostly figure.
- The line, if viewed as being infinite (in two directions... horizontal-vertical-or diagonal), has no measure of beginning or end or specialized distinction, unless at least one point is assigned to it... though it is typical that the value of "2" points is used.
- The Plane, if viewed as being infinite, typically receives 3 points in order to establish a coordinate identification.
As an aside reference, we might even include the 3 types of Armageddon scenarios the human mind has conjectured:
- Biblical (god/Heaven made) Armageddon.
- Nuclear (Man made) Armageddon.
- Terrestrial/Extra-Terrestrial (Nature made) Armageddon.
Alternatively, we can call the foregoing assumptions/postulates a concocted recipe, made up card game rules, ad hoc values, or fairy tales which have taken on a life of their own by way of being associated to/with actual events which humans can relate with/to, whether in a real sense, figuratively, or some "imaginated" neurotic/psychotic sensibility. The development of an assumption/postulate/conjecture/supposition... can be viewed in much the same way as an ancient human knocking one rock against another to form some object that is later applied to some usage which one or more others find useful and desirable; this is the case for geometry and counting which have been experimented with for thousands of years. Indeed, look at any present day idea with a widespread following and you will pay witness to a history of experimentation having forged the current usage... be it astronomy, chemistry, warfare, animal husbandry, farming, etc...
Eventually, like the chipping away at stones, or collecting of seashells on a piece of leather, or the development of a rudimentary toolbox and palette of colors used by a cave wall artist, a particular form... such as a triangle, or spherical object (e.g. necklace), is obtained and may later be attached to someone's neck, wrist, waist for ornamentation, or a bone or stick to become a club, an arrow or a spear. Such is the case for geometry and counting. While the rock, the stick and surface of a cave wall, tree, or mountain side are real, this is not the case for the point, line, and plane of geometry, nor the rudimentary values we know as 1, 2, and 3. When someone creates something that others find valuable and will trade for it, there often is the case in which a one-upmanship activity arises whereby the previous item is improved on or simply embellished by application and explanatory narrative by a more skilled sales-person who redefines or relabels or repackages the earlier idea, though it is retained in a basic form.
By reviewing multiple ideas in different time periods and contexts, we can look for similarities which are underscored by basic ideas, though they may occur in different forms with alternative words, symbols or combinations thereof, as well as absences and declarations of absences such as the notion of an "excluded middle". Where in some cases the trio of Rock- Scissors- Paper can easily be identified with the values of "zero-one-two" or "one-two-many" or even the single letters "R-S-P"; the point to be forwarded in the present context is that the trio, as a game, is widely known and played. Hence, it is not unreasonable to consider that it represents some underlying 3-patterned cognitive repetition which might show up in other contexts with different labels. It some cases you personally may not see an exact match between parallels suggested by someone else, but the fact that a similar patterning has been adopted also expresses the presence of a wide-spread behavioral activity adopted to whatever context and language the respective content is being used for. Hence, my assertion that the Pentadactyl limb references a standard Cognitive Model similar to the present discussion of extensions, elaborations, and embellishments of the Rock-Scissors-Paper theme.

Let us review some other Assumptions/Postulates regarded in other subjects in order to identify permutations and extensions that may incorporate definitions which obscure the similarity of a basic identity with respect to an underlying design giving the impression we are confronted by a cognitive template that I have previously labeled the Standard Cognitive Model.
- 3 fundamental axioms of chemistry, (are foundational to understanding how matter behaves and interacts in chemical reactions):
- Law of Conservation of Mass. (Conservation = 1)
- Law of Definite Proportions. (Proportionality = 2)
- Law of Multiple Proportions. (Multiplicity = 3/Many)
- 3 axioms of probability:
- 1st axiom, Non-negativity; The probability of any event (E) must be a non-negative real number.
- 2nd axiom, Normalization; The probability of the entire sample space Ω (all possible outcomes) is equal to 1.
- 3rd axiom, Countable Additivity; For any countable sequence of mutually exclusive (disjoint) events E1, E2 E3..., the probability of their union is the sum of their individual probabilities.
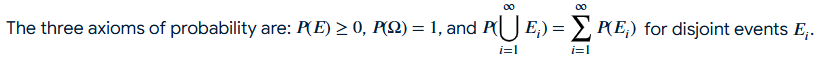
- 3 traditional axioms of logic:
- Law of (a single faced) Identity:
- This law states that something is what it is (A is A). Metaphysically, it means anything has a definite, non-contradictory nature. In propositions, if a statement is true, then it is true.
- Law of Non-Contradiction, (is not two-faced):
- This law asserts that something cannot be both true and false at the same time in the same sense (A is not non-A). Metaphysically, nothing can be both A and not-A. In propositions, a statement cannot be both true and false.
- Law of Excluded Middle, (is not single nor two-faced):
- This law states that for any proposition, either that proposition or its negation is true (either A or not A). Metaphysically, anything is either A or not A. In propositions, a statement is either true or false, with no middle ground.
- 3 axioms [or laws] of classical genetics (based on Gregor Mendel's work (on trait inheritance) in the 19th century):
- Law of Dominance: When an organism has two different alleles for a trait, the dominant allele is expressed.
- Law of Segregation: During gamete formation, alleles for a trait separate so each gamete gets only one allele. Offspring inherit one allele from each parent.
- Law of Independent Assortment: Alleles for different traits are sorted independently into gametes. The inheritance of one trait doesn't affect another.
- 3 axioms of Architecture, as defined by Vitruvius, are firmitas, utilitas, and venustas, which translate to strength, utility, and
beauty:
-
Firmitas (Strength);
- This refers to the structural integrity and durability of a building. A building must be able to withstand the forces of nature and time to be considered well-designed.
- Utilitas (Utility);
- This emphasizes the functionality and usability of a building. It should serve its intended purpose effectively and be comfortable and convenient for its occupants.
- Venustas (Beauty);
- This highlights the aesthetic appeal of a building, its pleasing proportions, and its harmonious relationship with its surroundings.
- Law of (a single faced) Identity:
- 3 "Axioms" or fundamental truths of barbecuing: Time- Temperature- Technique.
- 3 key axioms of Gaming are Players- Actions- Payoffs.
- 3 "Cosmic Sociology" axioms in the context of Liu Cixin's Three-Body Problem series:
- Survival is the primary need of civilization.
- Civilizations continuously grow and expand.
- The total matter in the universe remains constant.
3 Postulates (Axiomatic Declarations) of:
- Cell Theory:
- All living organisms are composed of one or more cells.
- The cell is the basic unit of structure and function in living organisms.
- All cells arise from pre-existing cells.
- Bohr's atomic model:
- Electrons orbit the nucleus in specific, stable paths called stationary states, with fixed energy levels.
- These orbits are only allowed when the electron's angular momentum is an integral multiple of h/2π (where h is Planck's constant).
- Electrons can only gain or lose energy by transitioning between these orbits, absorbing or emitting energy in discrete packets (photons).
- Dalton's atomic model (laid the foundation for modern atomic theory):
- All matter is composed of atoms, which are indivisible and indestructible.
- All atoms of a given element are identical in mass and properties.
- Compounds are formed by a combination of two or more different types of atoms.
- kinetic molecular theory of gases:
- Gases consist of tiny particles in constant, random motion.
- The volume of the particles is negligible compared to the space between them.
- Particles exert no forces on each other except during collisions, which are assumed to be elastic.
- Collision theory:
- Reactions occur due to collisions between reactant particles.
- Collisions must have sufficient energy (at least the activation energy) for a reaction to occur.
- Collisions must have the correct orientation for the reaction to proceed.
- Science:
- Empiricism: Scientific knowledge is based on observable and measurable evidence.
- Uniformity of Nature: The fundamental laws of nature are consistent across time and space.
- Testability: Scientific theories must be falsifiable through experiments.
- Kant's Moral Philosophy:
- Freedom: Humans have free will and are capable of making moral choices.
- Immortality: The soul continues to exist after death.
- God: A supreme being exists who is the source of morality.
- Characterized Formalism art and literature:
- Form over content: The primary emphasis is placed on the form and structure of an artwork, literary piece, or mathematical system, rather than on its content or meaning. Meaning is inherent in the way elements are arranged and organized, not in any external interpretation.
- Sharp focus: A focused analysis of the intrinsic qualities and elements of the work is demanded, excluding external factors like historical context, social influences, or personal emotions of the artist or observer. This allows for a more objective and analytical approach to understanding the work.
- Craft and technique: Emphasis on the execution and skill involved in creating the work is crucial. The importance of technique and craftsmanship in shaping the aesthetic impact and meaning of a piece is recognized, whether it's the brushwork in a painting or the logical deduction in a mathematical proof.
- Discussing Mathematics Foundations (Platonism posits that mathematical objects exist independently of human minds, while Formalism
views mathematics as a system of symbols and rules. Constructivism, on the other hand, emphasizes the role of human activity in creating
mathematical knowledge.):
- Platonism
- Core Idea: Mathematical objects and truths exist independently of human thought and are discovered, not invented.
- Analogy: Similar to how a geographer discovers existing geographical features, mathematicians discover pre-existing mathematical entities.
- Key Belief: Mathematical reality is ontologically prior to human experience.
- Formalism
- Core Idea: Mathematics is a system of formal rules and symbols, like a game with no inherent meaning.
- Analogy: A game of chess where the rules define the relationships between pieces, not any external reality.
- Key Belief: Mathematical statements are not about anything real; they are just manipulations of symbols according to predefined rules.
- Constructivism
- Core Idea: Mathematical knowledge is actively constructed by humans through experience and reasoning.
- Analogy: Building a house where each brick and beam is placed by a builder, creating the final structure.
- Key Belief: Mathematical truth is relative to human cognitive abilities and constructions.
Page initially created: Sunday, July 20th, 2025... 4:44 AM
Initial posting: Monday, Aug. 4th, 2025... 8:09 AM
- Platonism