(Basic Geometry of Cognitive Activity)
[1 point- 2 points- 3 points]
| RSP 1 | RSP 2 | RSP 3 | RSP 4 | RSP 5 | RSP 6 | RSP 7 |
Lookiloos as of August 4th, 2025
Both Geometry and Basic counting... not to mention higher or "pure" mathematics, are items of imagination like metaphysics, spirituality, and religion (as well as Eastern philosophy)... not to mention in particular, Buddhism, Christianity, Hinduism, Islam, and Judaism... very much in the manner of Astrology, Numerology, Palmistry, tarot cards, Psychology, Philosophy, Fairy tales, Myths, legends, and other genres of literature as well as Magic, Music, Art, Dance, and theater... all of which, like Military activity, interjects, adds, subtracts, multiplies, and divides bits and pieces of actual history and human behavior into convincing narratives of believable truth. All of them are concoctions made up by the imagination of humans like counting and geometry.
Needless to say, it is rather incredible that such nonsense, such superstition continues, until we make note of the fact that humanity has a history of sustaining belief in nonsense, readily represented by the centuries-long idea called Spontaneous Generation, to which we can assign other terrestrial directed ideas such as abiogenesis and Biopoiesis to as a trio of related vantage points of biological development. (Note: the concept of Panspermia relates to an extra-terrestrial origin for life's establishment and growth on Earth... Hence, we have a 3 to 1 ratio of ideas.)
The terms "spontaneous generation," "biopoiesis," and "abiogenesis" all relate to the origin of life, but have distinct meanings and historical contexts. Spontaneous generation was an early belief that complex life could arise from nonliving matter, a concept disproven by scientific experiments. Abiogenesis, on the other hand, is the scientific hypothesis that life originated from nonliving matter, specifically referring to the origin of the first simple life forms, not the spontaneous generation of complex organisms. Biogenesis is the principle that all living things come from other living things, a concept that contrasts with abiogenesis. Using the internet query "spontaneous generation, biopoiesis, abiogenesis", the following result emerges:
- Spontaneous Generation:
- This was a long-held belief that living organisms could arise from nonliving matter, like maggots from rotting meat or mice from grain.
- Historically, figures like Aristotle and Jean-Baptiste van Helmont supported this idea.
- It was disproven through experiments like those by Francesco Redi and Louis Pasteur, which demonstrated that life only comes from existing life.
- Abiogenesis:
- Abiogenesis is a scientific hypothesis proposing that the first life forms arose from nonliving matter.
- It doesn't suggest that complex organisms arise spontaneously, but rather that simple organic molecules formed and eventually evolved into the first living cells.
- Abiogenesis is a modern scientific concept, distinct from the discredited spontaneous generation theory.
- Biogenesis:
- Biogenesis is the principle that all living things originate from other living things.
- It is the foundation of modern biology and is supported by countless experiments and observations.
- Biogenesis replaced spontaneous generation as the accepted explanation for the origin of life.
In essence, while spontaneous generation was an old, disproven idea, abiogenesis is a modern scientific hypothesis that attempts to explain the origin of life from nonliving matter, and biogenesis is the principle that life comes only from other life.
An account which focuses on the topic of "spontaneous generation" as a long-enduring idea of nonsense believed in by respected scientists and deep thinkers of the past, is to be found in Daryn Lehoux's Creatures Born of Mud and Slime. From Aristotle's supposed origination of the spontaneous generation idea in the 300s BC era to the refutations of later centuries, we none-the-less find numerous so-called present day experts believing in very many notions of nonsense held up as truth, purity, and some ultimate excellence of thinking, within their respective and respected fields of study labeled as Mathematics, Physics, Astrology, Psychology, Philosophy, religion, Eastern philosophy, warfare strategy, etc...
Using the internet query "who finally refuted spontaneous generation?", we get the following response:
Louis Pasteur (19th Century) is credited with definitively refuting the theory of spontaneous generation. Through his swan-neck flask experiment, Pasteur demonstrated that microorganisms in broth came from airborne contamination, not from the broth itself. This experiment, along with his other work, showed that life only arises from pre-existing life.
While Pasteur is most recognized for this, other scientists like Francesco Redi and Lazzaro Spallanzani had previously contributed to the disproof of spontaneous generation. Redi's experiment with meat and flies in the 17th century showed that maggots did not arise spontaneously from rotting meat. Spallanzani, in the 18th century, improved upon Redi's work and further challenged the theory. However, Pasteur's work, with its elegant swan-neck flask experiment, is widely considered the definitive end to the debate.
It took hundreds of years, along with the developments in experimental methods and apparatus (such as the microscope), not to mention an unrecognized evolutionary development in human consciousness-driven conceptualization, before the nonsense of Spontaneous Generation was widely accepted. And this says nothing of the possibility that there may have been many people who are not recognized by any historical account, as having refuted the idea on their own, without the need for experimentation. There was simply no one paying attention to their views and they neither made a written account which survived and came to the attention of an historian, just like Gregor Mendel's work in genetics went unnoticed.
Internet query parameter... "gregor mendel's work went unnoticed":
Gregor Mendel's groundbreaking work on genetics was largely unnoticed during his lifetime primarily because his mathematical approach to inheritance and the concept of discrete, rather than blended, traits were not readily accepted by the scientific community of the time. Many scientists believed in the "blending theory" of inheritance, where offspring traits were seen as a mix of parental traits.
- Novel Approach:
- Mendel's use of mathematical and statistical analysis in biology was a new concept in the 19th century, and it was not widely understood or appreciated at the time.
- Blending Theory of Inheritance:
- The prevailing view was that traits blended together in offspring, resulting in intermediate characteristics. Mendel's experiments, however, showed that traits are inherited as discrete units (now known as genes) and can be dominant or recessive.
- Lack of Dissemination:
- Mendel's work was published in an obscure journal and his presentation at a scientific meeting didn't attract much attention.
- Focus on Darwin:
- The scientific community was heavily focused on Darwin's theory of evolution, which overshadowed other important biological discoveries.
- Lack of Direct Application:
- Mendel's work, while groundbreaking in its principles, didn't have immediate, obvious applications to the ongoing debates about evolution and heredity, further contributing to its neglect.
- Rediscovery:
- It wasn't until the early 20th century, when scientists like Hugo de Vries, Carl Correns, and Erich von Tschermak independently rediscovered Mendel's principles, that his work finally gained recognition.
There is no telling how many people in their day to day lives of growing plants, came to similar conclusions as the foregoing scientists, but excused their observations as a common sense perspective shared by others who like-wise did not speak of their views. Whereas we give credit to someone whose idea makes them money, or kills more people, or is a benefit to the sick, etc., it is not uncommon for those advancing an idea to have stolen it from someone else, either intentionally, or by way of some absent-mindedness, like many a writer who makes a comment that they may have read several books back in their past. Granted, events and ideas make impressions that we may at a moment forget where they arose from, though history gives them the credit someone else deserves. Many employees come up with ideas that a company or someone in a company takes credit for, just as surely as we see people being falsely blamed for a crime they didn't commit, or a crime is perpetrated by those wanting to cover up some other crime, as we have seen with governments, religions and businesses... not to mention the theft of ideas professors engage in by taking ideas from students whom they never give credit to.
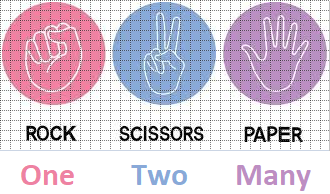
Whereas one idea leads to another, I find that I sometimes diverge along a path and lose sight of where I began, Thus let us return to the title of this page, with information culled from a basic internet query: "rock, scissors, paper or rock, paper, scissors?"
- "Rock Paper Scissors": is the most common name for the game in the US and UK.
- The game can also be referred to as "Scissors Paper Stone" in some regions, particularly in the UK.
- The name "Rochambeau" is used as an alternative name for the game rock-paper-scissors, especially in the western United
States.
- This usage is believed to be a reference to the Comte de Rochambeau, possibly because the game involves choosing between three options, much like the three-way alliance between France, the American colonists, and Spain during the war.
- Rochambeau was a French nobleman who served as a lieutenant general in the French army.
- He commanded the French expeditionary force that landed in Newport, Rhode Island, in 1780 to aid the American Continental Army.
- His troops, along with American forces led by George Washington, decisively defeated the British at the Siege of Yorktown, a pivotal moment in the war.
- After the war, Rochambeau returned to France and continued his military service through the early years of the French Revolution.
- Other names for the game include "roshambo," "ro-sham-bo," "bato bato pik," and "jak-en-poy", according to Wikipedia: Rock paper scissors.
The order of the words use in the three-part game can be viewed in terms of Linguistics as a reference to Word Orderusage and language/cultural preference, and/or to the order in which the associated basic enumeration occurs... in 1st, or 2nd, or 3rd place., just as we see alterations in how a person's name might be arranged such as in the case where the 3rd or last name is placed first, then the 1st and middle/2nd names... though variations can exist, and must at least be mentioned in the context of discussion basic cognitive patterning.
By using the internet query of "the 1, 2, Many early counting sequence", the AI system provided this information... however, it should be noted that earlier counting forms did not yet have either a "1" or a "2" and thus initially, the count may have been some model of plurality, later followed by a plurality + oneness, then a oneness, then a oneness + many/plurality, then a oneness + twoness, then a oneness + twoness + plurality/manyness...
The "1, 2, Many" counting sequence refers to a system used by some cultures where quantities are simply described as "one", "two", or "many", rather than precise numerical values beyond two.
- This system is characterized by:
- Limited Numerical Terms: It relies on a very small set of number words.
- Emphasis on Specific Small Quantities: It highlights the distinction between a single item, a pair, and a larger, unspecified group.
- Practicality for Basic Needs: For certain groups and situations, knowing the difference between one, two, or many might be sufficient for their practical needs, such as hunting or managing small groups of items.
- Example: The Pirahã counting system is described as using this "one-two-many" approach. Researchers who studied the Pirahã noted that they relied on these distinctions rather than a more extensive counting system.
- Significance— The "1, 2, Many" system provides insight into:
- Early Number Sense: It reveals a foundational level of mathematical understanding where the focus is on distinguishing small quantities rather than precise enumeration.
- Cultural Influence on Cognition: It demonstrates how cultural needs and linguistic structures can shape the development and expression of number concepts.
- Limitations:
- Inaccuracy for Larger Numbers: This system is not suited for accurately representing or communicating quantities beyond two, potentially leading to challenges when dealing with larger groups of items or complex mathematical tasks.
- Lack of Flexibility: It lacks the flexibility of more developed counting systems needed for advanced mathematical operations or abstract number concepts.

If a person pronounces the sequence of the game as Rock- Paper- Scissors, they are counting 1, 3, 2, according to the illustrated association of value. With respect to the Subject-Object-Verb word order sequence, they are all interchangeable in such a circumstance unless someone has a preference for labeling them as nouns. With respect to geometry, a person saying "rcck-paper-scissors" would be saying point-plane-line.
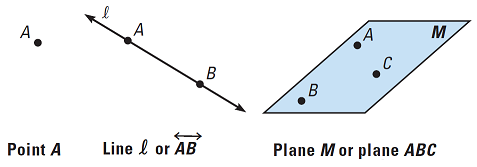
The widely played simple game known as Rock, Scissors, Paper, can be viewed as an ideological representation of basic geometry with its Point, Line, Plane, and these can alternatively be deduced... or let us say reduced to a basic model of enumeration which is used as a general expression of rudimentary counting efforts by early humans as "1, 2, Many". However, a problem can arise in the basic analogy upon reading some definitions of a point, line, plane in Geometry.
- A point is said to be a dimensionless location:
- Simply put, a point is said to have no actual size... no defining dimension, and can humorously be viewed as a ghostly or imaginative figure. Because it is sometimes defined as nothing... that is, a no "thing", its numerical value in this primitive sense means it is zero or even less than zero. However, since we do acknowledge it as existing, it therefore is a "thing" and must have some basic value such as 1.
- A line is said to be a one-dimensional figure extending infinitely in two directions:
- A basic line is not defined by any point if we view the line as an infinite structure of departure in two separate, or opposing directions, though it too is a ghostly or imaginative figure. Although one might want to suggest this is the surface of a very large object (like a circle that has no beginning or ending point), we don't know for sure. Adding one or more points to a line will alter its basic definition. A pair of scissors are two separate scissor lines attached at or by a point we can label as an intersection, or intersecting lines. A basic line is configurationally described as exhibiting the basic value of 2.
- A plane is said to be a two-dimensional surface extending infinitely in all directions:
- The third figure of our basic geometric trio is called a plane. It too is a ghostly and imaginative figure said to exist infinitely in two dimensions. And like the plane, its basic definition changes by adding a point to it. While Two points on a plane might be defined as a means of identifying a line, the use of three points changes the simple definition of a plane to a coordinate plane. 3 points are needed for introducing what can be described as the first plane (or "planar") type of complexity. The disposition of a plane being referenced as having a two-dimensional "infiniteness", is easily characterized has having the value of "many" or much, which is the successive value of being "3rd" in our count of the three ghostly or imaginative figures.
More simply put, we can define the point- line- plane as:
- A point has no length, width, or height. It's a (singular) dimensionless entity.
- A line is a one-dimensional figure that is straight, has no thickness, and extends infinitely in both directions. (it is commonly
- referenced with two points.)
- A plane is a flat, two-dimensional surface that extends infinitely in all directions. (It is commonly referenced with three points,
- labeled a coordinate system.)
So long as you look af the basic foundation of the ideological construct, you can see a cognitive parallel
The point, line, plane as Dimensionless, 1-Dimension, 2-Dimensions characters... Basic geometry is an early counting system using a set-of-three figurative elements. In multiple explanations of basic geometry you will see illustrations representing one, two, and three points as differentiations for the Point, the Line and the Plane:
It is of value to view the three basic geometric forms in an alternative way, which leads us into the realm of Physics:
- Let us assume the point is a rock.
- Let us assume the line is a string, slow moving stream of water, stream of consciousness or stream of time... to name but three of many alternative analogies one might use.
- Let us assume the plane is a sheet of glass, body of water, plain of consciousness, or dimensional fabric of time.
Let us say the first group of three basic geometric entities were the very first reality. However, it gets a bit tricky when we try to conceptualize onward, because we must consider whether and/or not each of the basic geometric entities are part of, come into contact with, or singularly represent a surface.
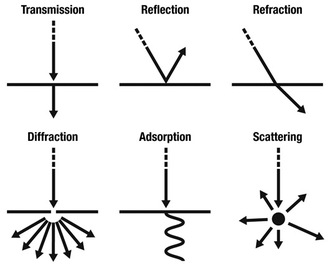
- For example, is the geometric "point" simply hovering about in a vacuumless space, or does it sit on a surface? In any event, is there a surface nearby to be distinguished as a separate entity or as part of the point's existence?
- Similarly, do the line and plane represent themselves in relation to a surface, or do they also exist as floating objects?
- If there is a "surface" to be distinguished, how does the point, line and plane interact with the surface?
- Are that which we see and label as a point, line and plane the result of Reflection? Absorption? Transmission? Or are we observationally experiencing a Refraction, Scattering or Diffraction?
It is now of value to think in terms of a second stage of reality as a progression:
- Let us assume the point can only find itself on a line if it is duplicated at some distance from itself as a reflected (bifurcated) image of acknowledgement.
- Let us assume the point can only find itself on a plane if it is triplicated at some distance from itself as a coordination.
- Let us assume we have created a 3-in-1 figure.
It is now of value to think in terms of a third stage of reality as a progression:
- Let us assume the point is a rock we have dropped on the line which is not broken in two, but vibrates, though the weight of the rock may cause it to also flex (bend) in the opposite direction.
- Let us assume that the line is a section of the plane which can vibrate, crack, reverberate, create undulations, waves, and concentricities, as well as fracture into fractal repetitions.
- Let us assume that each fractal excursion is a reflection or echo of the plane, line, and point.
- Let us now assume that this recurring trio can take on the appearance of different three-patterned activities and expressions such as the three dimensions of time (past-present-future), an assumed 3-stage progression of consciousness, etc...
Let us use the query "origin for the point, line, plane" to provide some basis for the collective identity:
- In geometry, a point has no dimensions, representing a specific location. A line extends infinitely in one dimension, connecting two
points. A plane is a two-dimensional, flat surface that extends infinitely, defined by three non-collinear points. Here's a more
detailed breakdown:
- Point: A point is the most basic element in geometry. It has no length, width, or height, only position. It can be represented as a dot or the intersection of two lines, according to Point, Line, Plane The fundamental elements of design. (Jimdo)
- Line: A line is formed by connecting two points and extending infinitely in both directions. It has one dimension: length. Think of it as a series of points aligned in a straight path. (Jimdo)
- Plane: A plane is a flat, two-dimensional surface that extends infinitely. It can be defined by three non-collinear points (points not lying on the same line) or a line and a point not on that line, according to Points, Lines, and Planes (Mathematics LibreTexts).
- A particle is a figment of human imagination but is frequently conjectured as a real entity such as for example, one might think about atomic particle not governed by the proposed Uncertainty principle.
- A line is a figment of human imagination and requires at least one imagined point to provide a distinction of plausibility, though it is typical to see the application of two imaginary points.
- A plane is a figment of human imagination and requires at least two points to provide a distinction of plausibility, though it is typical to see the application of three imaginary points.
Point–line–plane postulate (Wikipedia)
In geometry, the point–line–plane postulate is a collection of assumptions (axioms) that can be used in a set of postulates for Euclidean geometry in two (plane geometry), three (solid geometry) or more dimensions.
The following are the assumptions of the point-line-plane postulate:
- Unique line assumption: There is exactly one line passing through two distinct points.
- Number line assumption: Every line is a set of points which can be put into a one-to-one correspondence with the real numbers. Any point can correspond with 0 (zero) and any other point can correspond with 1 (one).
- Dimension assumption: Given a line in a plane, there exists at least one point in the plane that is not on the line. Given a plane in space, there exists at least one point in space that is not in the plane.
- Flat plane assumption: If two points lie in a plane, the line containing them lies in the plane.
- Unique plane assumption: Through three non-collinear points, there is exactly one plane.
- Intersecting planes assumption: If two different planes have a point in common, then their intersection is a line.
The first three assumptions of the postulate, as given above, are used in the axiomatic formulation of the Euclidean plane in the secondary school geometry curriculum of the University of Chicago School Mathematics Project (UCSMP).

History:
- The axiomatic foundation of Euclidean geometry can be dated back to the books known as Euclid's Elements (circa 300 B.C.). These five initial axioms (called postulates by the ancient Greeks) are not sufficient to establish Euclidean geometry. Many mathematicians have produced complete sets of axioms which do establish Euclidean geometry.
- One of the most notable of these is due to Hilbert who created a system in the same style as Euclid. Unfortunately, Hilbert's system requires 21 axioms. Other systems have used fewer (but different) axioms.
- The most appealing of these, from the viewpoint of having the fewest axioms, is due to G.D. Birkhoff (1932) which has only four axioms. These four are: the Unique line assumption (which was called the Point-Line Postulate by Birkhoff), the Number line assumption, the Protractor postulate (to permit the measurement of angles) and an axiom that is equivalent to Playfair's axiom (or the parallel postulate).
- For pedagogical reasons, a short list of axioms is not desirable and starting with the New math curricula of the 1960s, the number of axioms found in high school level textbooks has increased to levels that even exceed Hilbert's system.
Internet query: "how many postulates of basic geometry are now being used in public schools?"
In the context of typical high school geometry courses in public schools, the number of postulates used is not fixed by a single, universal standard like Euclid's original five postulates. Modern geometry curricula often present a greater number of postulates to provide a more complete and rigorous foundation for the subject. Some common postulates found in current high school geometry textbooks and curricula include:
- Ruler Postulate: Establishes the relationship between points on a line and real numbers, enabling measurement of distances.
- Segment Addition Postulate: States that if point B is between points A and C, then AB + BC = AC.
- Protractor Postulate: Relates rays in an angle to a protractor, allowing for the measurement of angles.
- Angle Addition Postulate: Indicates that if a point D lies in the interior of angle ABC, then the measure of angle ABD plus the measure of angle DBC equals the measure of angle ABC.
- Through any two points, there exists exactly one line.
- Through any three non-collinear points, there exists exactly one plane.
- Parallel Postulate: States that through a point not on a line, there is exactly one line parallel to the given line.
These postulates, along with others related to the properties of points, lines, planes, and angles, provide the foundational assumptions upon which theorems are built and proofs are constructed in geometry courses taught in public schools. The specific number and phrasing may vary slightly between different textbooks and curricula.
In short, students around the world are subjected the requirement of an elaborated fairy tale system of indoctrination established as some sort of truth standard for the assumptions of a given type of logic which society has framed itself in accordance with and expects everyone to comply with, or be ostracized as a person with inferior intellect... so much so that standards of attendant mathematics are required as defining goal posts of intellectual ability and achievement used as an exclusionary postulate for making someone inadmissible to a given field of study. What a bunch of malarky.
Here we are confronted by a basic cognitive pattern being exercised under the guise of different theatrical productions of the human mind with players wearing different garments and using made up languages to express the same underlying pattern being overlooked. So let us move sideways at the time when geometry was being developed in order to see how the same mental pattern is being played out in religion....
- Unique point assumption of geometry in religion is called god.
- Unique line assumption of geometry in religion is called a path.
- Unique plane assumption of geometry in religion is called by many names:
- Heaven
- Nirvana
- One with the creator
- Ambrosia (drink of the gods for immortality)
- Enlightenment
- Jannah/Paradise
- Happy Hunting Ground
- Immortality
- Moksha/Mukti
- alignment with Tao/the flow... free of cyclicity
- Valhalla
- etc...
- The Plane of Religion [Heaven (etc.) is often affixed with three coordinate points such as:]
- Trinity, Triune, Three Jewels, 3 spiritual divisions, etc...
- The Line of Religion is often affixed with two points resulting in numerous dichotomies:
- good/evil, god/satan, right/wrong, moral/immoral, gods/goddesses, etc...
- The Point of Religion is often affixed with a special name or the speciality of having no name: Ineffable One,
- God, Allah, Enlightenment, The Beyond, or "beyond the beyond the beyond", Creator, Father, Transcendence,
- Ultimate Reality, Xanadu, Sky world/country, Celestial abode, etc...
The same basic pattern using an associated 1-2, 3/many, counting theme can be seen in Geometry, Religion, Myths, Fairy tales, Sports, various literatures, governments, commerce, education, art, music, philosophy, etc... and yet no one is even looking at biology and physics to notice the similarity of basic patterning as it relates to the development of Earth tha first had a fast rotation and now has a slower rotation, which caused a 3-patterned cyclicity of stroboscopic irradiation life has had to adapt to as a survival mechanism, as is readily seen in the usage of a DNA triplet code and 3 Germ Layers... along with the presence of a 3-to-1 ratio.
By illustrating one example of direct analogical proportionality, you might better recognize the the simplistic style of geometry being employed by all Western Religions and Eastern Philosophies because their practitioners are simplistic/elementary geometers (geometricians of a primitive age):
- The Holy spirit is the point.
- The Holy Son is the line (or path).
- the holy Father is the plane.
The foregoing three are a list of basic geometrically aligned assumptions which go no further than being an asserted series of postulates that one might find written on a chalkboard in a mathematics class, but the teacher doesn't actually know how to teach the geometry of spirituality beyond a simple declaration they took out of some religious text claiming to be a "gospel" of higher and purer revelation. Every single practitioner of some assumed greater pathway to a higher consciousness and realization of more purposeful fulfillment are all elementary thinkers of spirituality. None of them recognize that they are incapable of teaching the geometry of spirituality beyond the basic assumptions which they repetitiously prosletyze, thinking that this method of recitation is somehow a mantra which will advance them to a greater understanding and realization their present model of spirituality is elementary school arithmetic whose instructors want to give their students that they are more knowledgeable than they actually are, by talking about the presence of spiritual postulates they don't know how to effectively apply in creating a system of higher spiritual mathematics with its appropriate geometry which must be graphically displayed beyond the present kindergarten finger counting recitals and expectations for everyone to recite as the standard mantra.
Page initially created: Sunday, July 20th, 2025... 4:44 AM
Initial posting: Monday, Aug. 4th, 2025... 8:11 AM