~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
Yet, just like sequential counting in that there may be no quantity beyond a thousands place (interpreted as a four-quantity), we can find examples which may include but not exceed a ten thousands place, whereby some interpret this as a five, but could readily be interpreted as a 4 to 1 or 3 by 2. For example, while some people say we have five fingers, another person may count the digits as four fingers and one thumb. Still another person may single out one or more fingers as have some particular distinction (pinky, ring finger, middle finger), whereby the described count takes on a different proportion. The point is, while we humans may be counting in one fashion, Nature may be "thinking" of quantity or functionality in a different fashion. In any respect, the aforementioned repetitive usage of a dichotomous orientation being used by Mathematicians may be a false configuration which acts as an obstacle to further development. We know how to look, but we don't know how to see. Our seeming obsession of using dualities as an underlying standard of mathematics appears to be a Westernized recitation of a differently styled yin/yang compilation over-which we embellish with patterns-of-three to provide us with the scenario that we add, subtract, multiply or divide one number in conjunction with another number in order to get a presumed third. I say "presumed" because humans rationalistically orient themselves towards adopting an attitude of an accomplished or achieved progression, when in actuality it may be little more than an adaptation to an overlooked incremental deterioration requiring a specific type of survival mechanism.
When one sees set figure sequences such as (1...), (1, 2...) (1, 2, 3...) and think this is a reflection of superior mathematics and not some repetitive cognitive illustration found in other subjects which use their own vernaculars to express the same pattern; how are we truly going to be able to discern a progressive development in mathematical thinking if we are simply using the same underlying patterns expressed with different symbols regulated as part of a larger survival mechanism that has been forced into usage by the presence of an incrementally deteriorating environment which most people would readily dismiss by using one or another rationalization as a defense mechanism?
This is not to say that mathematics doesn't have great utility, much like a stick used by a chimpanzee to flesh out a tidy morsel of an insect from some crevice, but the long term facility of such an adaptive behavior benefiting an individual in their respective life, ineffectually provides them with an ability to notice that the assumed progress defined by tool usage also embraces a foolhardy interpretation about the prospects of longevity for the entire species. In the world of chimpanzees, the usage of a stick can be useful... just like the usage of mathematics for humans. In this sense, mathematics is little more than a type of stick with which humans can probe, poke at and doodle a myriad of geometric forms with and call it science, art, poetry, music or even futility.
No less, let us view Nature itself (that which humans recognize in the context of our reality) as a primitive life form or life form originator which uses primitive patterns, whereby human deductions of basic patterns routinely portray the exhibition of small numbers (for example, we have a triplet DNA code and not a larger number code), which may thus reflect a stagnant developmental sequence that some readers might dismiss as due to the length of time required for Evolution to make changes. Yet, it is not certain if Evolution can make changes to its own Nature... that is, provide life forms with a different model of Evolution with which to evolve, or use some other mechanism other than that which we at present call "Evolution". Indeed, why do we see so many recurring small number patterns in basic Natural phenomena and yet attempt to dismiss this notion by claiming there are larger number patterns (beyond 1s, 2s, 3s, 4s, 5s...) such as the 8 (octet) pattern in chemistry, the 8 pattern in (octomerous) life forms, and the 7 or 8 quantity of Hox genes in free-living members of Platyhelmiths (Acoelomorphs have four or five Hox genres: pg. 292, Integrated principles of Zoology, ISBN 978-8-07-304050-9) yet fail to recognize that such an "8" pattern apparently occurs more often in primitive instances and is not widespread in multiple other subjects? And to this we might add the presence of a primitive "4" occurrence in quadripedalism with a lowered number bipedal gait used as a criteria for judging evolutionary advancement, at least in primates.
For example, why isn't there 8 families to atomic particles or people routinely being born with eight fingers, eight toes, eight eyes, eight heads, hearts, etc.? Why no eight-coding system for DNA and RNA? Why no 8-forms of DNA or a standardized 8-speed bicycle or 8-position selection on appliances and automatic transmissions, or eight children being born as a standard birthing quantity of all life forms or 8 cores as a standard in all computers? Why does Nature stop at using a recurrence of small number patterns unless for some reason it actually doesn't, and it is human perception/consciousness which is imposing the recurrent usage of small number patterns? Why does mathematics, not only in the presence of an infinity of numbers and a suite of small numbers to choose from (zero through nine), set a standardized dominant focus on using dichotomies, much in the same manner as the usage of a binary system for an electric circuit based computer language? Are mathematicians simply regurgitating some ancestral obsession of using patterns-of-two (like some Western born Yin/Yang formula), and will rationalize some presumed value to describe why such is the case, without taking the time to statistically arrive at a value which makes such a usage an improbability, or that such a probability is indicating we are dealing with an influence that is being overlooked? In other words, is the system of mathematics rigged to configure a mathematical rationale to offer some plausible reason for the persistent usage of an underlying dichotomization of views implanted in the construction of mathematics equations, typically resorting to some biological, atomic or mechanistic model to offer up a supposed proofing exposition?
We can recognize a recurrence of different patterns being use to express ideas in all subjects. All of them have some level in which basic patterns of a given subject matter are being indexed and in some cases such as comparative anatomy and embryology, we come to discern similarities of patterns exhibiting the same quantity. This is not to say that researchers are making the correct deductions, but that... nonetheless, some pattern is offered as being exemplary of a given process, function or design. At least how humans are perceiving such occasions. All told, we are dealing with information which can be filed under a heading of information theory that, not surprisingly, encompasses a usage of number relationships:
(Information theory is a) a mathematical representation of the conditions and parameters affecting the transmission and processing of information. Most closely associated with the work of the American electrical engineer Claude Shannon in the mid-20th century; information theory is chiefly of interest to communication engineers, though some of the concepts have been adopted and used in such fields as psychology and linguistics. Information theory overlaps heavily with communication theory, but it is more oriented toward the fundamental limitations on the processing and communication of information and less oriented toward the detailed operation of particular devices.
The formal study of information theory did not begin until 1924, when Harry Nyquist, a researcher at Bell Laboratories, published a paper entitled "Certain Factors Affecting Telegraph Speed." Nyquist realized that communication channels had maximum data transmission rates, and he derived a formula for calculating these rates in finite bandwidth noiseless channels. Another pioneer was Nyquist's colleague R.V.L. Hartley, whose paper "Transmission of Information" (1928) established the first mathematical foundations for information theory.
Clearly, the recurrence of number patterns in different subjects is information that we do not yet understand what is being conveyed to us. While the information is being transmitted just as electrical impulses of the early telegraph, suggesting that the patterns being revealed are like a type of Morse code or Braille, we have also come upon a circumstance reflecting the causal nature of certain patterns being more frequently repeated than others. Does such a situation reflect a primivity of thinking or an accurate depiction of a phenomena indicating we are subjected to a primitive formula of Nature in the present context of Earth, and that other forms of Nature exist with more complex formulations of processes, functions and structures?
While humans have unraveled the code of genetics and atomic particles (to some extent), the patterns being presented to us by recurrences in different subjects is not understood because such a discipline of study is in the position where all subjects begin such as for example paleontology. Whereas there may have initially been one or two who collected a few bones and used them as door-stops (so to speak), later on there were those who collected more bones and other items (which were later labeled as fossils), and still others who eventually saw the collections as representative of a pattern of life and geologic stratification. For example:
Paleontological research dates back to the early 1800s. In 1815 the English geologist William Smith demonstrated the value of using fossils for the study of strata. About the same time, the French zoologist Georges Cuvier initiated comparative studies of the structure of living animals with fossil remains. ("paleontology." Encycloædia Britannica.)
All present day disciplines had their formative beginnings with fits and fashions, starts and stumbles, as well as detractors. Whereas Charles Darwin (for example) made a collection of life forms while on his five year voyage: (The HMS Beagle was a) British naval vessel aboard which Charles Darwin served as naturalist on a voyage to South America and around the world (1831–36). The specimens and observations accumulated on this voyage gave Darwin the essential materials for his theory of evolution by natural selection. ("Beagle." Encyclopædia Britannica.)
If Darwin had not made the trip or had not made a collection with which to refer to, it is suspect whether he would have developed his "On the Origin of Species by Means of Natural Selection" (later called a theory of Evolution), even though the publication of the idea took two decades after his initial three-volume beginning and after he gained the distinction of being a Justice of the Peace. ("Darwin, Charles." Encyclopædia Britannica.) The point is others were not only thinking along the same lines, but were gathering dispersed amounts of examples which would later prove to help enlarge the underlying premise of Darwin's ideas. All the collections were necessary even if he did not yet have a conceptual framework for inclusion in his own ideas. Needless to say, the rather disparate looking information began to fit together into a puzzle from which a picture of life could be ascertained, and is extensively applied today.
The recurrence of enumerated patterns and those patterns not yet enumerated are presenting us with a sketch we can tentatively describe as representing a blueprint or map or etching of human cognitive activity. If you prefer, let us call it a paint-by-numbers dot-to-dot illustration that we have not collected all the numbers for in their respective placements. If low numbers being exhibited in ideas of fundamental occurrences represent that Nature itself is a primitive life form (so to speak), let us also identify what sort of species this life form is and whether it is able to evolve to a more modern formulation. If Mathematic's usage of a top-heavy dichotomous orientation is to be viewed as a fundamental/basic scaffolding, then is this due to an imposition created by the human psyche, the indication of an inherent disposition due to a primitive design (like an expressed development using two instead of three germ layers), or a relative "cry for help" because mathematics is being forcibly subjected to an imprisonment which forces it to curtail its desire for expressive freedom?
The relatively small group of number patterns being used in different subjects is a puzzle whose answer may or may not lie in retracing our thoughts in addressing other kinds of puzzles with an underlying numerical reference.


(The Konigsberg bridge problem is) a recreational mathematical puzzle, set in the old Prussian city of Königsberg (now Kaliningrad, Russia), that led to the development of the branches of mathematics known as topology and graph theory. In the early 18th century, the citizens of Königsberg spent their days walking on the intricate arrangement of bridges across the waters of the Pregel (Pregolya) River, which surrounded two central land-masses connected by a bridge. Additionally, the first landmass (an island) was connected by two bridges (5 and 6) to the lower bank of the Pregel and also by two bridges (1 and 2) to the upper bank, while the other landmass (which split the Pregel into two branches) was connected to the lower bank by one bridge (7) and to the upper bank by one bridge (4), for a total of seven bridges. According to folklore, the question arose of whether a citizen could take a walk through the town in such a way that each bridge would be crossed exactly once.
In 1735 the Swiss mathematician Leonhard Euler presented a solution to this problem, concluding that such a walk was impossible. To confirm this, suppose that such a walk is possible. In a single encounter with a specific landmass, other than the initial or terminal one, two different bridges must be accounted for: one for entering the landmass and one for leaving it. Thus, each such landmass must serve as an endpoint of a number of bridges equaling twice the number of times it is encountered during the walk. Therefore, each landmass, with the possible exception of the initial and terminal ones if they are not identical, must serve as an endpoint of an even number of bridges. However, for the land-masses of Königsberg, A is an endpoint of five bridges, and B, C, and D are end-points of three bridges. The walk is therefore impossible.
It would be nearly 150 years before mathematicians would picture the Königsberg bridge problem as a graph consisting of nodes (vertices) representing the land-masses and arcs (edges) representing the bridges. The degree of a vertex of a graph specifies the number of edges incident to it. In modern graph theory, an Eulerian path traverses each edge of a graph once and only once. Thus, Euler's assertion that a graph possessing such a path has at most two vertices of odd degree was the first theorem in graph theory.
Euler described his work as geometria situs—the "geometry of position." His work on this problem and some of his later work led directly to the fundamental ideas of combinatorial topology, which 19th-century mathematicians referred to as analysis situs—the "analysis of position." Graph theory and topology, both born in the work of Euler, are now major areas of mathematical research.
"Königsberg bridge problem." Encyclopædia Britannica article by Stephan C. Carlson, Professor of Mathematics, Rose-Hulman Institute of Technology, Terre Haute, Indiana. Author of Topology of Surfaces, Knots, and Manifolds: A First Undergraduate Course.
Although the foregoing presented us with a "7" problem, we need to contrast this with problems exhibiting a configuration of three elements, to which let us add the three shells and card monte games problem, the dichotomous "checks and balances" schematic to provide a solution involving the three (Executive, Legislate, Judicial) branches of government, the And, Or, Not logic circuitry problem, the God- Humanity- Satan problem, the Christian Trinity problem, as well as the following:

From celestial mechanics we have the 3 body problem and from Mathematics we find three classical problems. (Note, the exercise I am providing concerning the part played by the incremental deteriorations of the Sun- Earth- Moon complex with respect to the usage of a top-heavy reliance on dichotomies used as a an accommodating survival mechanism, is another type of 3-body problem).
The three-body problemThe inclusion of solar perturbations of the motion of the Moon results in a “three-body problem” (Earth-Moon-Sun), which is the simplest complication of the completely solvable two-body problem discussed above. When Earth, the Moon, and the Sun are considered to be point masses, this particular three-body problem is called "the main problem of the lunar theory," which has been studied extensively with a variety of methods beginning with Newton. Although the three-body problem has no complete analytic solution in closed form, various series solutions by successive approximations achieve such accuracy that complete theories of the lunar motion must include the effects of the non-spherical mass distributions of both Earth and the Moon as well as the effects of the planets if the precision of the predicted positions is to approach that of the observations. Most of the schemes for the main problem are partially numerical and therefore apply only to the lunar motion. An exception is the completely analytic work of the French astronomer Charles-Eugène Delaunay (1816–72), who exploited and developed the most elegant techniques of classical mechanics pioneered by his contemporary, the Irish astronomer and mathematician William R. Hamilton (1805–65). Delaunay could predict the position of the Moon to within its own diameter over a 20-year time span. Since his development was entirely analytic, the work was applicable to the motions of satellites about other planets where the series expansions converged much more rapidly than they did for the application to the lunar motion.
"celestial mechanics." Encyclopædia Britannica. Article by Stanton J. Peale, Professor of Physics, University of California, Santa Barbara.
The three classical problems(H.O.B. note: notice Euclid used two items as a means of expressing a pattern-of-two styled dichotomy.<)/p>
Although Euclid solves more than 100 construction problems in the Elements, many more were posed whose solutions required more than just compass and straightedge. Three such problems stimulated so much interest among later geometers that they have come to be known as the “classical problems”: doubling the cube (i.e., constructing a cube whose volume is twice that of a given cube), trisecting the angle, and squaring the circle. Even in the pre-Euclidean period the effort to construct a square equal in area to a given circle had begun. Some related results came from Hippocrates (see Sidebar: Quadrature of the Lune); others were reported from Antiphon and Bryson; and Euclid's theorem on the circle in Elements, Book XII, proposition 2, which states that circles are in the ratio of the squares of their diameters, was important for this search. But the first actual constructions (not, it must be noted, by means of the Euclidean tools, for this is impossible) came only in the 3rd century BC. The early history of angle trisection is obscure. Presumably, it was attempted in the pre-Euclidean period, although solutions are known only from the 3rd century or later.
"mathematics." Encyclopædia Britannica. Article by Wilbur R. Knorr, Professor of the History of Science, Stanford University, California. Author of Ancient Tradition of Geometric problems and others.
Here we have an example of three logic functions applied to an underlying dichotomy of zeros and ones in electrical circuitry for computer languages.
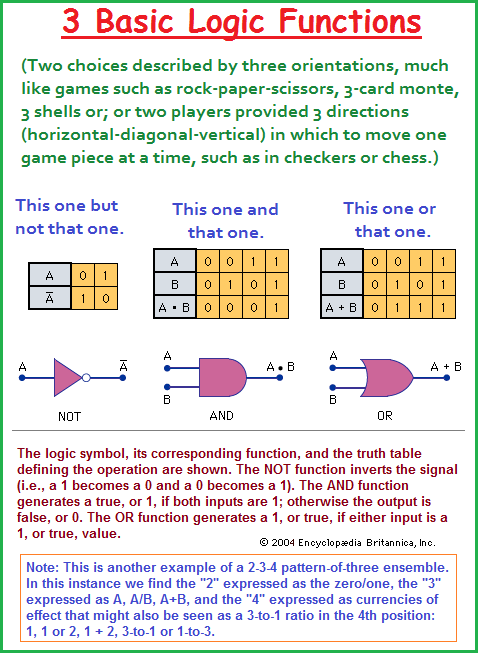
While the And- Not- Or logic circuit presents us with a pattern-of-three formulation, when speaking of electrical circuitry we often encounter two underlying models labeled as AC (alternating current) and DC (Direct current). Hence, we are presented with a dichotomy to which we can add a few others:
- open/closed circuit
- Hot/Ground (also neutral). A color code for a DC circuit is that the Red wire is positive and the Black wire is negative. In an AC circuit, you might frequently find a black wire for positive or "hot" side and a white wire for the negative (non-hot) side. A green wire might be used for a grounding wire.
- Series/Parallel
- (While we have the idea of a "short" circuit to indicate a faulty one, we do not customarily say "long" circuit as a means to convey the idea of a non-short- circuit.)
If counted separately a person arrives at five different types of circuits, but upon recognizing the presence of dichotomies, we see there are 3, or at least 2 and one-half. Metaphorically speaking, it presents us with an overall circuitous route similar to the quantity of terms one might find in the human cochlea (snail-like process in the ear), attendant with the usage of electrical, mechanical and fluidic types of circuitry used in the process of hearing.
With respect to patterns-of-two and math puzzles, we find a "classical" representation in what is called the The Prisoners' Dilemma. It is of need to note the problem present us with (at the very leas) the problem of a dichotomy over which is inscribed over with three possible alternatives, much like a binary computing language adopting the usage of three alternatives (And- Or- Not), with multiples being used as an expressed circumvention.

The study of dualities is an important perspective of analyzing human cognitive activity but it must be done in the larger context of collating the several (but extremely limited) variety of enumerated examples to be found in multiple subject areas, even if an author(s) does not use number and instead) whether consciously or unconsciously) uses symbols or words or an overall writing/illustration portrayal of enumeration. For example, the recurring usage of a basic heading- body- ending profile is typically used, as well as the period- question mark- exclamation point patterns-of-three. In other words, an author can use Dichotomization without even being aware of doing so, because they take such a pattern as normal, usual and customary.
Here is an example of what can be described as an illustration concerning the development of enumeration:
Verse Forty Two
Wing-Tsit Chan, 1963
- Tao produced the One.
- The One produced the two.
- The two produced the three.
- And the three produced the ten thousand things.
The ten thousand things carry the yin and embrace the yang, and through the blending of the material force they achieve harmony.
People hate to be children without parents, lonely people without spouses, or men without food to eat, And yet kings and lords call themselves by these names. Therefore it is often the case that things gain by losing and lose by gaining. What others have taught, I teach also: "Violent and fierce people do not die a natural death." I shall make this the father of my teaching.
Here's another variation:Threes poster column 5
*** Laozi (author of Tao Te China): Dao produces one. One produces two. Two produces three. Three produces the ten thousand things. (In classical Chinese, the "ten thousand things" means "everything." Commentators have long disagreed over what the "one, two, and three" refers to, usually plugging in their favorite cosmological, cosmogonic, or metaphysical model.) Laozi further writes: Something amorphous & consummate existed before Heaven & Earth. Solitude! Vast! Standing alone, unaltering. Going everywhere, yet unthreatened. It can be considered the Mother of the World. I don't know its name, so I designate it "Dao." Compelled to consider it, name it "Great." (Dao is considered indistinct & undefinable. It is not the vision of a visionary that helps others see more clearly, but that which they are able to articulate from memory of their visionary trek.)
In the above expression we can note that the counting sequence describes a 1- 2 -3... many grouping. Altogether it is a set... that is, a singular set of a singular idea and not a single idea quantifying a multiplicity of examples. While it can be argued that "ten thousand things" references a multiplicity, the sequence itself is a single cognitive set. It is the same sort of "set theory" from which our present human mathematics is derived. It is not a singular set of multiplicities nor multiple sets of singularity. All three are different models of cognitive orientation. the present mathematics being used around the Earth is based on a primary orientation where the "two" is the dominant theme where the "many" is describe as three or more, even though some mathematicians use a (1,2,3...) as a recurring cognitive set, and our series of notated numbers uses three items before demarcating them from the next three such as in the case of ones-tens-hundreds (comma) thousands-ten thousands- hundred thousands (comma)... etc...
Then again, does counting quantitative sets instead of a singular set constitute a greater complexity of thinking to be approximated with a "higher" form of conceptualization from which can arise a "better" mathematics... particularly when a presently used mathematics is mastered by those asserting there is no greater model to be born from a biologically based encephalization process?
Despite my short digression from the main presentation of Mathematics being stagnant, let me provide an example from Biology concerning the repetition of a dual-based division of multiplication with respect to cell generation. Whereas one might well characterize development by way of such a two-patterned development scenario as Natural and Normal as well as dynamic, the repetitious usage of the same pattern suggests a stagnant design. Though the two-patterned design (just like in mathematics and psychology) has utility, this does not detract from the observation that what we are perceiving is a stagnant model. Similarly, we see a stagnant model in DNA with its reliance on a triplet code, instead of evolving towards the usage of another pattern. The lack of change, the lack of such a dynamic, leads me to consider that such patterns are being reinforced by pressures which require such low number repetitions to occur as a survival mechanism. However, because we can note that the overall Sun/Earth/Moon complex is on a course of incremental deterioration, it may well serve us preferentially to conclude that we are dealing with a tell-the-tale design of accommodation... whereby our ideas involving mathematics, psychology and other subjects, take on the position of being rationalizations which delude us into thinking we are engaged in activities of sustained survivability when actually we are not.
The dichotomizations being used in Mathematics (and other subjects) indicate human conceptualization is in a state of stagnant repetition reminiscent of an early counting scheme which the three-patterned phrase of "one-two-many" can suffice as a generality exhibiting humanity's initial developmental attempts to forge a trail into the conceptual grasp of group or set theory initiated by a behavior of pairing and then simply addition, such as is expressed in the Fibonacci series conveyed as an exercise of mathematical playfulness that may have been thought of as a serious intellectual formulation by Fibonacci himself.
One of the (dichotomously) oppositional stances one might take against the present discussion is to point out that we typically align human life in concert with a previous era's interest in geology, whereby the life span (origination and ultimate extinction) is typically assessed in terms of a geological standard of time stratification. In other words, it is very common to typically see life in conjunction with some geological period, whereby geology is the standard by which we come to judge a life form's survivalness. Occurrences of different Life forms is expressed in geological terms such as the following images describes as an example of this modeling, though one must look with a different type of perspective to discern the usage of singularity to multiplicity as well as stratifications encompassing the ideas of from left to right and top to bottom, though one could easily flip/flop these ideas around:


For some readers, the geologic time scale coupled with the belief that the Sun/Earth/Moon (3-body) complex has been around from billions of years and is estimated (by way of educated guesstimation) to remain for billions of more years, since there is no indication (according to present day determinations) that we should suspect any dramatic alteration to occur suggesting a shorter period of time is to ensue, barring some unforeseen cataclysmic occurrence. However, the means by which mathematics was developed by what I believe to have been a single model of counting expressed in culturally adopted different ways of presentation, describes a lineage of cognitive descent much like so many other lineages seen in biology... from a singularity of multiplicity by way of using a pairing model as an underlying model over which a triadic or "many" expression is used to embellish the one-two formula. From the value of three onward appears to suggest a multiplicity, though it might be argued that a "two" instance is a multiplicity of one, though multiplicity typically becomes defined in terms of three or more,occurring with different symbols and labels. Yet, the multiplicity appears to be governed by a conservation which repeats itself... often by way of doubling itself.
As it is, Mathematics is a model of cognitive activity which developed by way of an associative pairing such as pairing one item with a representative word or symbol that came to stand for the object or item being observed, such as one apple. While I do not know how long it took humanity to develop the concept of one or singularity in terms of a conscious acknowledgment of it being a quantity, nor the sequence of time events before the concept of two, and so forth came to mind, or if there was some sort of "Eureka!" moment of conceptualization for one or more quantity identities emerging consecutively or jointly; the point is that we of today can appreciate that the developmental scenario of numbers was a progression... even if there were one or more individuals who gained a more comprehensive grasp of enumeration and quantity prior to their peers. It may well have been the case that past eras, deep into the recesses of hominin development there were those whose ability to conceptualize exceeded their counterparts and may have brought about occasions for them to be subjected to ostracism, trephination or even death, as a coping mechanism for those whose inability to grasp what was being (crudely?) expressed and felt was an indication of something being wrong with a particular individual who did not maintain the visual perspicuity of the many, particularly the reigning leadership.
In any respect, I am claiming that the present models of mathematics are a divergent lot which originate from a single model of counting whose adaptability for future conditions is limited and that the present usage of mathematics to persistent in efforts to survive by encouraging all social activities to "do the math" according to the prevailing axioms, also limits the ability of present human societies to adapt to changes requiring a model of mathematics which is born from a different model of counting. Yet, because present social authority imposes the belief among the public that the current model of thinking mathematically is a vital necessity, any other model which may surface due to a developmental change in human consciousness will be oppressed to comply and leading to misunderstood conflicts of conceptualized orientation.
By viewing present Mathematics as a type of game with a given set of rules that become mastered by a few while the majority come to struggle with, it is believed that those who come to master mathematics are somehow more intellectually astute or even gifted, while the rest of humanity, the majority of humanity, does not have the intellectual fortitude to learn the rules and apply them according to the dictates of those who have become convinced by their math instructors and thus instruct others with the same message that a thorough grasp of higher mathematics is needed to work competently in many fields of research. Even though it is realized that mathematics is a contour of thinking that can be expressed within the parameters of different mediums such as art and music, mathematics is not typically viewed as a genres of art and musical composition using an alternative set of symbols, language and application. Even while it is known that those skilled in the use of an abacus can perform simple calculations equal to other processes, the abacus, as an expressed model of computational effort is not typically acknowledged as a model of language medium, just as are musical instruments and the instruments used by artistic illustrators.
If Humanity encounters a sentient species born on a different planet, it may well be the case that their kind of mathematics may have originated by way of a different model of counting. Whereas humanity began the trek of its mathematics along non-set progressions, a counting methodology which uses set progressions would be one in which larger amounts of information are taken into account. The sets would not also exhibit a volume of objects to be counted, but a volume of objects/entities with more referencing to the originations of multiple complexities. In other words, while one child is on a trek of developing a mathematics by way of counting wooden blocks, and another is on a different path defined by counting sets of different kinds of blocks with different labels. Such a situation is made more difficult when we have child development experts who have created what are called developmental milestones which are used by multiple others to gauge the developmental performance of children by their corresponding ability to perform a task according to guidelines that an adult observer may not be competently able to deduce that a given child is enabled to mentally use a different model for developing rudimentary counting associations. The problem is made more acute because society is governed by a present model of mathematics which sees the world through a predominant two-patterned prism/kaleidoscope governed by axioms which are initiated in accord with such a binary orientation. Society and social behavior is exhibited to conform to this model because leaderships in business, government and religions expect compliance to their alternative forms of dichotomization such as qualitative/quantitative products and productivity, Patriotism/Treason, good/evil, etc...
Another problem with the foregoing stated reliance of orienting human existence to a geologic scale is to overlook the possibility that human life-span as a species might be better off in describing itself in terms similar to the life-cycle of a vinegar (fruit) fly, which has a relatively short life span (of about two weeks in duration). I mention the fruit fly not only because it has been used extensively in genetics experiments but also in a metaphorical sense because of its two wings, though other two-winged life forms might be used to express the notion of "flightedness", which can be used to illustrate the phenomena known as pure math and its suggested "loftedness" and ability to soar above conventional (applied) mathematics; such as the view I believed to have been illustrated by Godfrey Harold harding in his distaste for applied mathematics because he viewed pure mathematics as an exalted character, in line with those who think that mathematics is the Queen of all other subjects.
Regarding the question of how we might develop a "better" mathematics in terms of creating conditions for improving the quality of life by creating society in accord with such a mathematic's, is first to recognize that the present mathematics has an origin based on a formula that comes to assert itself as a dominant theme in the practices of business, government and religion. By being made aware that the current model of mathematics is a limitation that it is but a species of cognitive activity which may be akin to a primitive mentality... as one might describe the human brain having developed along a three-patterned (Paul MacLean-nian styled triune brain complex) course of Reptilian- Mammalian- New-mammalian, then one might come to view mathematics in a state of primivity it can not grow out of. Like a developmental stage experienced by those life forms which use some type of cocooning process (to give but one type of analogy), the current model of mathematics is a primitive stage which is binding human development too... as if humanity mentality is akin to a cyclic state awaiting some change in the environment to trigger its further development; despite many who would claim that humanity's model of mathematics is a fully developed butterfly (along with the moths and skippers which make up the insect order Lepidoptera), winging its way from the nectars of different subject-flowers. (Skippers are considered an inter-mediate form between moths and butterflies.)
When I speak of a "Dynamic Calculus", I am not referring explicitly to the model of mathematics named Calculus. Calculus as defined by a Britannica on the subject is stated as: (Calculus is a) branch of mathematics concerned with the calculation of instantaneous rates of change (differential calculus) and the summation of infinitely many small factors to determine some whole (integral calculus). As defined, this does actually pertain to the development of Mathematics, unless for some reason a reader thinks Mathematics was developed instantaneously (spontaneously). In the sense that I am using the word, it refers to the whole of mathematics as a type of calculating methodology which one might refer to as a tree with multiple branches and shoots from its roots or as a single species with different racial classifications, or as a library with different genres of books, magazines, newspapers, etc...
When using a biology metaphor to describe mathematic's development from a basic (what I presently believe to be) singular origin, one might also be inclined to continue using the analogy to present the view that mathematic's may be exhibiting not a fully-fledged development but some pre-stage position of its metamorphoses. Then again, if we look at the underlying skeleton (blueprint/scaffolding) of mathematics as expressed by its heavy usage of cognitively described dualities, one might want to say this equates with a basic cellular doubling event or a bilateral body plan, of which we may note the existence of 3 types of body plans viewed from different vantage points, though the two-word phrase "body plan" is not characteristically used in several of the contexts from which the following thimble-full of examples have been culled:
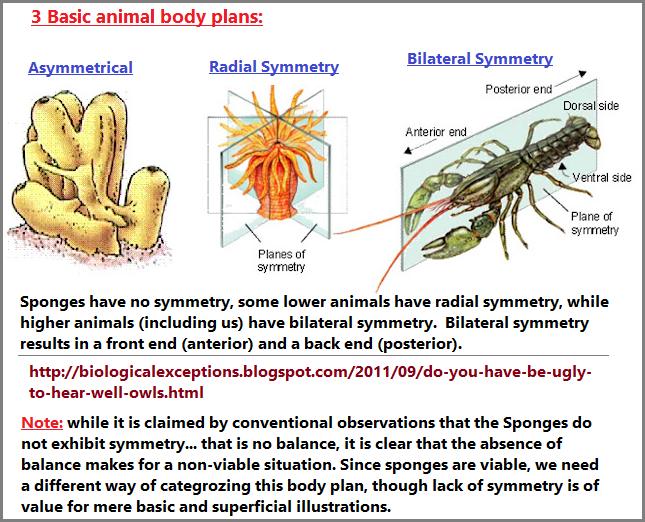

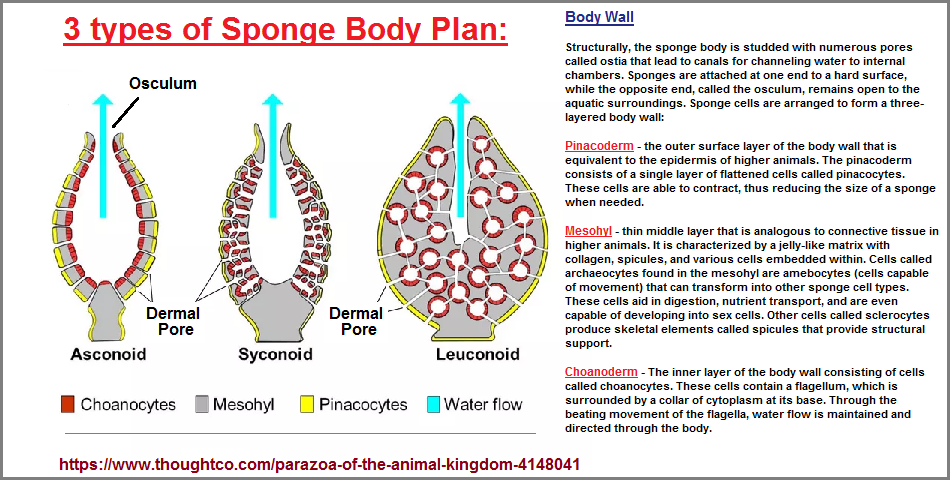
Although the foregoing example of sponge body plans would seem to indicated that this represents a fundamental structure, it needs to be placed into the larger context of other animal body plans which are described by the quantity of Germ layers, namely diploblastic (two layers) and triploblastic (three layers). The usage of an underlying two-patterned orientation found in mathematics, computer language and other subjects, suggests we are dealing with the prominent presence of a diploblastic formation found in the development body plans of the cnidarians (sea anemones, corals, and jellyfish) are diploblastic, the inner endoderm and outer ectoderm being separated by an acellular mesoglea. ("circulation." Encyclopædia Britannica.) A triploblastic model of development is said to occur in animals from earth worms to humans, while Porifera (sponges) and Placozoa, lack clearly defined tissues and organs, (yet) their cells specialize and integrate their activities. ("animal." Encyclopædia Britannica.) And though the term "Monoploblasitic" (one germ layer) is not part of the routine vocabulary of comparative anatomy/embryology, let us nonetheless make note of it including the idea that in some perspectives, the sponges are considered to be a representative animal thereof. In other words, we see an increase in germ layer quantity from simple to complex life forms. Similarly, let us speculate that a prominent usage of two-patterned ideas found in Mathematics and other subject areas provides us with the consideration we are dealing with a circumstance of primivity... unless, like in embryological studies, the prominent usage of such is like a student that has a preoccupation with the body functions which arise from the 2nd, middle (mesodermal) layer, though in actual evolutionary terms, it appears to have occurred third in the overall developmental sequence, even while some other researchers claim the neural crest as a forth germ layer. However, the neural crest(s) is said to arise due to groupings of ectodermal cells, developed as a column on each side of the neural tube. ("nervous system, human." Encyclopædia Britannica.)
In several cases one may find illustrations exhibiting a simple numerical pattern that might otherwise be viewed as a set (set of one, set of two, set of three, etc...), though in different applications the actual quantity of layers, departments, structures, levels, forms, compartments, distinctions, appendages, etc., may be fewer or several more when viewed from a different vantage point. Nonetheless, the standard cognitive formula appears to be the usage of only a few— such as one, two, three or multiples thereof, but infrequently as a large quantity seen as a standard repetition in multiple subjects. For example, though mathematics has an infinity of numbers at its disposal, most equations are formulas advancing simple patterns configured into assumed complexities like someone playing chess, checkers, or a card game against themselves or multiple imaginary players, which entail different types of betting, bargaining, baiting, in order to best some effort set as an objective before them... and frequently appears to be like a child with an imaginary playmate carrying on either/or silent/outspoken dramatized conversation. Examples of this are when someone talks to their vehicle accusingly or in a manner trying to coax out another mile before they run out of gas that may alternatively be measured in terms of full, half, quarter and eight of a tank of gas, unless some other system of measurement is employed. Another example is when someone tries to beat themselves at a previous (sports, exercise or other) record, likely using some numerical indexing formula. Mathematicians are not exempt from competing against themselves to pursue some "higher ground" of formulaic accomplishment.
Yet, we also see lots of mimicry which we might use to explain the recurrence of a few numerically indicated patterns cropping up in different subjects. Even the exceptions to recurring patterns is a recurring pattern with a low quantitative repetition. For example, we might speak of the recurring Octet formula found in chemistry, but don't see the value "8" as a wide-spread occurrence of notability as we do other patterns such as twos and threes. Whereas we can witness a lot of people engaging in the activity (in different contexts) using one enumerated value that is added, subtracted, multiplied or divided from/to/with another number quantity to arrive at a third actual or approximation, they may nonetheless use an unrealized adherence to a formulated dichotomous theme. Whether one examines musical notation or the notation sometimes employed in the counting of squares in checkers or chess, the latter two refile on a system of play dictated by being able to move playing pieces in one of three directions noted as horizontal, diagonal and vertical, with musical notion often subscribing to the formula of using fractions and not enlarged sets of whole numbers.
Whereas we are dealing with the language of mathematics, one can also look at common verbal expressions involving grammar which can be subsumed under the heading of linguistics, though in terms of grammar, Noam Chomsky's "tansformational grammar" idea can be reviewed to identify the established usage of a dichotomy called Surface and Deep structures, though one might also refer to the dichotomy of consonant and vowels, which are "added" together to produce syllables whereby a third feature known as suprasegmentals arise. In addition to this "two" notation found in language, we find the idea of word order in Linguistics distinguishes three-patterned linear orders of arranging a subject, object and verb.
These are all (six) possible word orders for the subject, object, and verb in the order of most common to rarest (the examples use "she" as the subject, "loves" as the verb, and "him" as the object):
- SOV is the order used by the largest number of distinct languages; languages using it include Japanese, Korean, Mongolian, Turkish, the Indo-Aryan languages and the Dravidian languages. Some, like Persian, Latin and Quechua, have SOV normal word order but conform less to the general tendencies of other such languages. A sentence glossing as "She him loves" would be grammatically correct in these languages.
- SVO languages include English, Bulgarian, Macedonian, Serbo-Croatian,[10] the Chinese languages and Swahili, among others. "She loves him."
- VSO languages include Classical Arabic, Biblical Hebrew, the Insular Celtic languages, and Hawaiian. "Loves she him."
- VOS languages include Fijian and Malagasy. "Loves him she."
- OVS languages include Hixkaryana. "Him loves she."
- OSV languages include Xavante and Warao. "Him she loves."
(Wikipedia: Word Order)

The following (1st list) list comes from (What is Word Order?), which I truncated into fewer word association compilations. The link provides information on the three-patterned word order idea, yet presents a seventh category called "free word order". Yet if one looks at this assumed "free-ness", it too must contain one of the six claimed in the foregoing Wikipedia article, unless one is speaking without using a subject, object or verb as distinctions. However, if these three are used, there are only six possibilities unless one alternatively uses different types of word categories or uses a pattern-of-one or a pattern-of-two combination method such as using only one-word or two-words instead of three. It is an intellectual juggling mechanism seen in every single subject, be it mathematics, philosophy, politics, religion, etc...

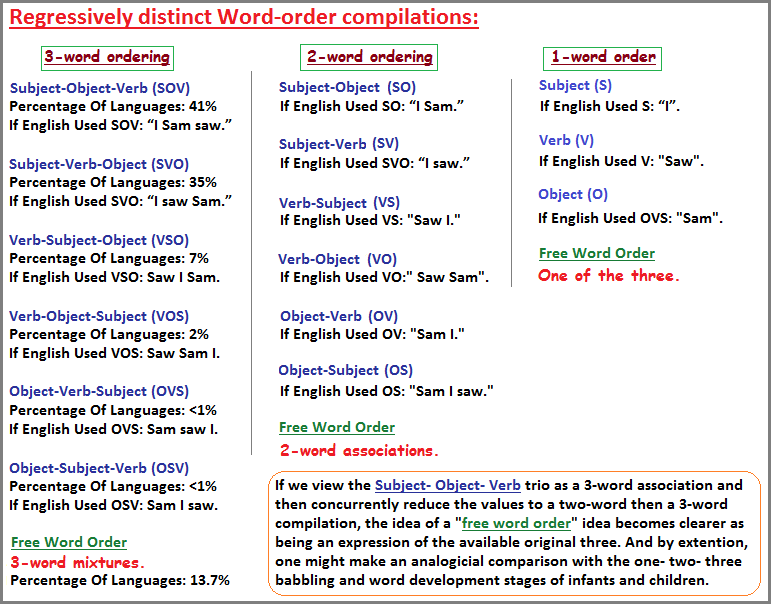
The idea of a "Free" word order needs to be seen as a cognitive orientation that has many parallels if we group the different variations of the 3-patterned Subject-Object-Verb as a separate triad identity... so to speak, and the idea of a separate "free" category as a different identity... this combination can be seen as a 3-to-one complex or as a duality. These Identities might not come to mind as patterns if we are looking only for compatibilities in a single subject area. However, if we look beyond the territory of a single subject area, we come face to face with similarities which can be viewed in the context of illustrating a repetition of cognitive behavior. This link (3-to-1 ratio examples) and the following example illustrating another "free" reference, clearly indicate similar cognitive patterns in different subject areas:
Date of Origination: 19th March 2022... 5:23 AM
Secondary page split: 24th March 2022... 3:24 AM
Updated Posting: 2nd January 2023... 11:01 AM Initial Posting: