~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
Let me reiterate. I refer to present day Mathematics with all its many derivations called disciplines, as representing a stationary or static profile and is thus not developing, otherwise to be viewed as non-moving or non-dynamic. It is of need to recognize the distinction between a new form of mathematics and mathematically-inclined craftsticians who simply adopt new ways of using the older forms; much like a person alternatively using a knife as a fork and spoon as opposed to someone who actually creates new implements using these labels. While the underlying basic intended usage is the same, the structure of both a fork and a spoon provide for a greater utility of a basic idea, while an overall value count stops at three utensils. In other words, there appears to be a limited cognitive profile being expressed by all of humanity, albeit with different labels and different forms in different contexts.
 |
 |
The three-patterned Knife- Fork- Spoon ensemble can be looked upon as symbolic representations of quantity and thus enumeration. For example, the knife can easily be seen as a "1" figure, the fork, etymologically speaking, can characteristically describe a "2" by deducing the word "fork" in terms of a branching effect that must be understood in the early (developmental) models of forks with two tongs or tangs that were later joined by others, but always in a limited sense, and the word "spoon" can be seen as a model of quantity in that it can hold a large quantity described as "much" or "many" or heap or pile of: (e.g. soup, gravy, mashed potatoes, peas, etc...). Note: while it may not be historically referenced as a possibility, let me suggest that the origination of the fork as a twin-pointed object may have initially occurred as a one-upman-ship exercise to be more than a single knife, and thus was a two-pronged knife in the beginning, but was eventually transformed to be a separate utensil.
In the same vein of thinking, the usage of a spoon may have arisen as a means to take in a larger portion (in a diminutive way) for the mouth, when sipping soup from a cup or dish was thought to be an expression of being poor and thus termed a social vulgarity... all to the joy of utensil makers. Whereas we today have different types of knives, forks and spoons used for particularized settings, they are not different implements. In other words, the three basic ones remain, with no actual "4th" one added to the count. Nor can we include the usage of two chopsticks, which is not a natural cognitive design in the sense of being absent from widely dispersed different cultures. And the usage of three fingers to eat with by some Middle Eastern peoples where water for washing utensils is a scarce commodity, necessarily incorporates the knife, fork, spoon trio in their one (right) hand.
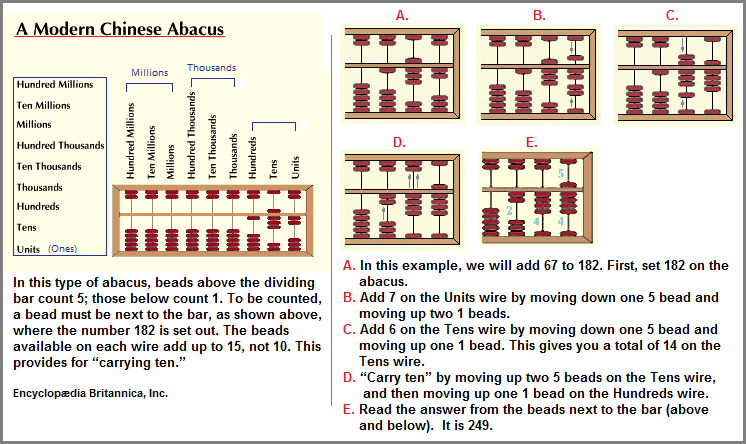
It is a need to view the abacus in its basic layout where the "important" (larger) values are placed to the top, as if expressing a bottom-to-top or bottom-up orientation. I point this out in order to compare the orientation of the abacus to column structures used throughout history in architectural settings, as if the columns were different versions of a wired abacus being used as an unrecognized cognitive exercise involving simple counting schemes, where form and manufacture consisted of basic, addition, subtraction, multiplication (repetition) and division, and ornamentation sometimes used as one might apply a linguistic embellishment, frequently seen when some mathematicians engage in a "confrontation" with an equation which may prove to be some felt to be engaging in intimidation, boasting, and other personality models. First, let us look at a small measure of history concerning the abacus.

(The Abacus is a) calculating device, probably of Babylonian origin, that was long important in commerce. It is the ancestor of the modern calculating machine and computer. The earliest "abacus" likely was a board or slab on which a Babylonian spread sand so he could trace letters for general writing purposes. The word abacus is probably derived, through its Greek form abakos, from a Semitic word such as the Hebrew ibeq ("to wipe the dust"; noun abaq, "dust"). As the abacus came to be used solely for counting and computing, its form was changed and improved. The sand ("dust") surface is thought to have evolved into the board marked with lines and equipped with counters whose positions indicated numerical values—i.e., ones, tens, hundreds, and so on. In the Roman abacus the board was given grooves to facilitate moving the counters in the proper files. Another form, common today, has the counters strung on wires.
The abacus, generally in the form of a large calculating board, was in universal use in Europe in the Middle Ages, as well as in the Arab world and in Asia. It reached Japan in the 16th century. The introduction of the Hindu-Arabic notation, with its place value and zero, gradually replaced the abacus, though it was still widely used in Europe as late as the 17th century and survives today in the Middle East, China, and Japan; an expert practitioner can compete against many modern mechanical calculating machines. ("abacus." Encyclopæ:dia Britannica.)
Now let's take a look at the item called a column, which not only reminds me of the "columns" of beads used in an abacus, but also because the word "abacus" shows up when speaking about column orders. The article may be lengthy for some of today's readers who want information condensed to a bit or bite size since they either do not have the necessary intellectual stamina, are just plain mentally lazy, or practice the view that they have some above average intelligent intuitive ability to grasp the main gist of a topic from an outlined review or synopsis. By habit, many readers would just gloss over the comments regarding the activities of column designers' using mathematical efforts described by such terms as adding and multiplying, but also the use of geometry. algebra and calculus. Since the present topic is about the Philosophy of Mathematics, it is important to point out and make note of how the presence of mathematics can show itself in multiple venues, and either suggests there is some underlying biological reason (such as displayed by the geometry of a spider's web), or it is merely a cultural artifact being imposed on people to carry out their lives "under the whip" (so to speak) of mathematical thinking as if it were a political correctness and social language requirement to set one above and away from the crude thinking of those who do not routinely use mathematics as a cognitive tool. Much like Latin is still used in some cases of scientific expression, or having the knowledge of using two or more languages when most others use only one. The adopted usage of a second (or multiple) language(s) (like mathematics) is sometimes used as an egotistical posturing affectedness.
Again, so that I may intentionally belabor the point, the following needs to be read as if one is reading a mathematical story problem, as a means of emphasizing the presence of enumeration that might otherwise not be thought of as a mathematical expression. On many occasions a person may encounter the reverence that there are three main types of columnar capitals named the Doric, the Ionic, and the Corinthian. Other accounts display variations of these three, resulting in five orders. Needless should it be for me to say, but Architecture is Mathematics exercised by the hands to create a form readily accessible to the eyes, heart and soul.
Also called order of architecture
Any of several styles of classical or Neoclassical architecture that are defined by the particular type of column and entablature they use as a basic unit. A column consists of a 1) shaft together with its 2) base and its 3) capital. The column supports a section of an entablature, which constitutes the upper horizontal part of a classical building and is itself composed of (from bottom to top) an 1) architrave, 2) frieze, and 3) cornice. The form of the capital is the most distinguishing characteristic of a particular order. There are five major orders: Doric, Ionic, Corinthian, Tuscan, and Composite.
There are many separate elements that make up a complete column and entablature. At the bottom of the column is the stylobate; this is a continuous flat pavement on which a row of columns is supported. Rising out of the stylobate is the plinth, a square or circular block that is the lowest part of the base. Atop the plinth and forming the remainder of the base are one or more circular moldings that have varying profiles; these may include a torus (a convex molding that is semicircular in profile), a scotia (with a concave profile), and one or more fillets, or narrow bands.
The shaft, which rests upon the base, is a long, narrow, vertical cylinder that in some orders is articulated with fluting (vertical grooves). The shaft may also taper inward slightly so that it is wider at the bottom than at the top.
Atop the shaft is the capital, which serves to concentrate the weight of the entablature on the shaft and also acts as an aesthetic transition between those two elements. In its simplest form (the Doric), the capital consists (in ascending order) of three parts:
- The necking, which is a continuation of the shaft but which is set off from it visually by one or more narrow grooves;
- The echinus, a circular block that bulges outward at its uppermost portion in order to better support the abacus;
- The abacus itself, a square block that directly supports the entablature above and transmits its weight to the rest of the column below.
The entablature is composed of three horizontal sections that are visually separated from each other by moldings and bands. The three parts of the entablature (in ascending order) are called the 1) architrave, 2) frieze, and 3) cornice.
The unit used in the measurement of columns is the diameter of the shaft at the base; thus, a column may be described as being eight (lower) diameters high.
Ancient Greek architecture developed two distinct orders, the Doric and the Ionic, together with a third (Corinthian) capital, which, with modifications, were adopted by the Romans in the 1st century BC and have been used ever since in Western architecture:
- The Doric order is characterized by a slightly tapered column that is the most squat of all the orders, measuring in height (including the capital) only about four to eight lower diameters. The Greek forms of the Doric order have no individual base and instead rest directly on the stylobate, although subsequent forms of Doric frequently were given a conventional plinth-and-torus base. The Doric shaft is channeled with 20 shallow flutes. The capital, as stated before, consists of a simple necking; a spreading, convex echinus; and a square abacus. The frieze section of the Doric entablature is distinctive. It is composed of projecting triglyphs (units each consisting of three vertical bands separated by grooves) that alternate with receding square panels, called metopes, that may be either plain or carved with sculptured relief's. The Roman forms of the Doric order have smaller proportions and appear lighter and more graceful than their Greek counterparts.
- The Ionic order differs from the Doric in having more flutes on its shaft and in the scrolls, or volutes, that droop over the front and rear portions of the echinus in the capital. The echinus itself is carved with an egg-and-dart motif. The height of the entire Ionic order— column, base, capital, and entablature— is nine lower diameters. The base of the column has two tori (convex moldings) separated by a scotia. The shaft, which is eight lower diameters high, has 24 flutes. On the entablature, the architrave is usually made up of three stepped fasciae (bands). The frieze lacks the Doric triglyph and metope, and hence this area can hold a continuous band of carved ornament, such as figural groups.
- The Corinthian order is the most elegant of the five orders. Its distinguishing characteristic is the striking capital, which is carved with two staggered rows of stylized acanthus leaves and four scrolls. The shaft has 24 sharp-edged flutes, while the column is 10 diameters high.
- The Tuscan order is a Roman adaptation of the Doric. The Tuscan has an unfluted shaft and a simple echinus-abacus capital. It is similar in proportion and profile to the Roman Doric but is much plainer. The column is seven diameters high. This order is the most solid in appearance of all the orders.
- The Composite order, which was not ranked as a separate order until the Renaissance, is a late Roman development of the Corinthian. It is called Composite because its capital is composed of Ionic volutes and Corinthian acanthus-leaf decoration. The column is 10 diameters high.
The Doric and Ionic orders originated nearly simultaneously on opposite shores of the Aegean Sea; the Doric on the Greek mainland and the Ionic in the Greek cities of Asia Minor. (The volutes of the Ionic capital were adapted from Phoenician and Egyptian capital designs.) The Doric may be considered the earlier order of the two only in its developed form. Both orders originated in temples constructed out of wood. The earliest well-preserved example of Doric architecture is the Temple of Hera at Olympia, built soon after 600 BC. From these beginnings, the evolution of the stone Doric column can be traced in architectural remains in Greece, Sicily, and southern Italy, where the Doric was to remain the chief order for monumental buildings for the next eight centuries.
The Greeks as well as the Romans regarded the Corinthian as only a variant capital to be substituted for the Ionic. The first known use of a Corinthian capital on the outside of a building is that of the choragic Monument of Lysicrates (Athens, 335/334 BC). The Corinthian was raised to the rank of an order by the 1st-century-BC Roman writer and architect Vitruvius.
The Romans adopted the Doric, Ionic, and Corinthian orders and modified them to produce the Tuscan order, which is a simplified form of the Doric, and the Composite order, which is a combination of the Ionic and Corinthian orders. Another Roman innovation was the superposed order; when columns adorned several successive stories of a building, they were normally of different orders, in an ascending sequence from heaviest to most slender. Thus columns of the Doric order were assigned to the ground floor of a building, Ionic ones to the middle story, and Corinthian or Composite ones to the top story. To avoid the complications of separate orders for each story, the architects of the Renaissance invented the Colossal order, which is composed of columns extending the height of two or more stories of a building.
Vitruvius was the only ancient Greek or Roman writer on architecture whose works survived the Middle Ages. When his handbook for Roman architects, De architectura, was rediscovered in the early 15th century, Vitruvius was at once hailed as the authority on classical architecture. Based on his writings, Italian architects of the Renaissance and Baroque periods developed an aesthetic canon that established rules for superposing the classical orders. The architects also laid down rules for the proportions of the orders and their parts down to the most minute members. The exact proportional dimensions of every element of an order was specified, so that, given the diameter of the column or any other dimension, the entire order and all of its separate elements could be reconstructed through routine calculations. The rules were thus carried to extravagant lengths that were undreamed of by the Greeks and rarely observed by the Romans.
Succeeding artistic periods witnessed revivals of the archaeologically "correct" use of the orders, though many architects continued to use the various orders with the utmost freedom. In Modernist architecture of the 20th century, the orders passed from use as superfluous ornament, their structural functions having been taken over by columns and piers made of steel or reinforced concrete. ("order." Encyclopædia Britannica, Ultimate Reference Suite, 2013... No specific author is listed for the article.)
In establishing some modicum of understanding the existence of a planetary influencing pattern, it is of need for the reader to visualize the Sun blazing down on Earth as it is spinning much faster in the past the it does today. Visually, the triple-patterned stroboscopic effect of a fast spinning Earth (billions of years ago) coupled to an intense Sun (conjectured as a likely candidate for the production of a triple code in the developmental scenario of DNA and the one-two-three sequence of Germ layer development0, will continue to create the situation where the two-patterned night/day sequence is elongated further into an effectual one-pattern— to the eventual point where the Earth stops spinning and the Sun is thought to have expanded in its white Dwarf stage thus consuming the innermost three planets (Mercury, Venus, Earth).
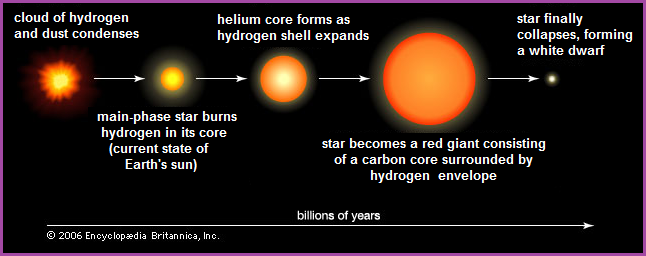
The Sun has been shining for 4.6 billion years. Considerable hydrogen has been converted to helium in the core, where the burning is most rapid. The helium remains there, where it absorbs radiation more readily than hydrogen. This raises the central temperature and increases the brightness. Model calculations conclude that the Sun becomes 10 percent brighter every billion years; hence it must now be at least 40 percent brighter than at the time of planet formation. This would produce an increase in Earth's temperature, but no such effect appears in the fossil record. There were probably compensating thermostatic effects in the atmosphere of Earth, such as the greenhouse effect and cloudiness. The young Sun may also have been more massive, and thus more luminous, and would have lost its early mass through the solar wind. The increase in solar brightness can be expected to continue as the hydrogen in the core is depleted and the region of nuclear burning moves outward. At least as important for the future of Earth is the fact that tidal friction will slow down Earth's rotation until, in four billion years, its rotation will match that of the Moon, turning once in 30 of our present days.
The evolution of the Sun should continue on the same path as that taken by most stars. As the core hydrogen is used up, the nuclear burning will take place in a growing shell surrounding the exhausted core. The star will continue to grow brighter, and when the burning approaches the surface, the Sun will enter the red giant phase, producing an enormous shell that may extend as far as Venus or even Earth. Fortunately, unlike more massive stars that have already reached this state, the Sun will require billions of years to reach this state.
The process of energy generation results from the enormous pressure and density at the centre of the Sun, which makes it possible for nuclei to overcome electrostatic repulsion. (Nuclei are positive and thus repel each other.) Once in some billions of years a given proton (1H, in which the superscript represents the mass of the isotope) is close enough to another to undergo a process called inverse beta decay, in which one proton becomes a neutron and combines with the second to form a deuteron (2D). This is shown symbolically on the first line of equation 1, in which e- is an electron and V is a subatomic particle known as a neutrino.
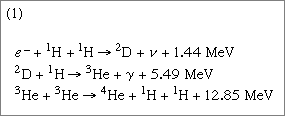
While this is a rare event, hydrogen atoms are so numerous that it is the main solar energy source. Subsequent encounters (listed on the second and third lines) proceed much faster: the deuteron encounters one of the ubiquitous protons to produce helium-3 (3He), and these in turn form helium-4 (4He). The net result is that four hydrogen atoms are fused into one helium atom. The energy is carried off by gamma-ray photons (ɣ) and neutrinos, V. Because the nuclei must have enough energy to overcome the electrostatic barrier, the rate of energy production varies as the fourth power of the temperature. ("Sun." Encyclopædia Britannica. )
(The foregoing equation presents us with the deuteron (2), Helium (3), Helium (4). It is a 2-3-4 ensemble that shows up elsewhere: Devil's advocate page 14.
However, the repetitions we are seeing in physical and mental activity to the point of suggesting humanity has reached the outskirts of its abilities may not actually represent human capacity in term of potential, but human possibility because of its confinement to an environment which is incrementally deteriorating. It is the combined (3-body) deteriorations of the Sun- Earth- Moon interactions which are forcing life forms on Earth to adopt a formula of adaptation which permits it to gain and sustain the necessary type of equilibrium for existing in such conditions as a rationalistic survival mechanism. Even while different life forms may come to fully realize that they are on a course of sequential extinction, they hold their chins up... so to speak, and face the eventuality with the unrecognized distinction of a species-specific model of rationalization. In terms of humanity, though it recognizes the eventual distinction to come, it rationalistically creates views, beliefs and practices which provide a model of assumed progress to be gained. For example, on the one hand many humans think in terms of an eventual Nature-driven apocalypse or a man-made disaster, many humans also secure for themselves the rationale that they will then enter into a heaven, a paradise, a transcendence, a nirvana or some-such other model of presumed progressive stage of development. It's as if the stages of development which life forms pass through act as an underlying model from which is garnered the idea that the present existence is yet one stage to develop out of into a next one, much like the evolutionary development which life forms have experienced, such as from a diploblastic (two germ layers) to a triploblastic (three germ layers) state of developmental existence (from which we can presume there at one time existed what may be called a "monoploblasitic" stage, even if it was little more than an aggregation of collected-in-one-spot processes).
Whereas comparative embryology and overall anatomical designs exhibit a routinization of similar patterning, even if the initial deductions were incorrectly interpreted to represent a holistic idea that later became recognized as a fragment of the overall collection as in the case of Ernst Haeckel and his biogenetic law which expressed the view that "ontogeny recapitulates phylogeny—i.e., the development of the animal embryo and young traces the evolutionary development of the species". ("biogenetic law." Encyclopædia Britannica Ultimate Reference Suite, 2013.) It was an interesting holistic view in his era of exploration but later became altered to be describe a much smaller venue of development stated as "embryonic ontogeny recapitulates embryonic phylogeny". Below is an illustration of Haeckel's collection of different animal life forms exhibiting similarities.
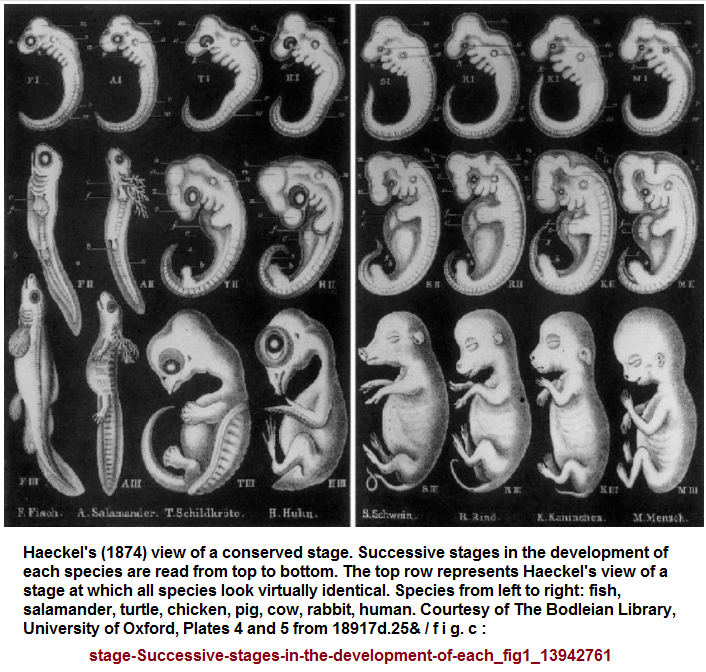
While later observers criticized the collection as a fraud, the idea was nonetheless not only unique, but a representation of a cognitive orientation as a recurrence in the human brain. The orientations were similarly dualistic in their basic formulation such as encountered in other subject areas using characterizations such as from left-to-right, top-to-bottom, inside-to-outside, early-to-late, primitive-to-complex, mouth-to-anus, etc., including the reversal of such ideas. The point is, by taking one example from the foregoing list, is it Natural for humans to think (hear, see, taste, feel, write, etc...) in a left to right fashion, or is this an imposed formula of an underlying "two"-based compartmentalization of mental processing?
Similarly, whereas some may say that the drivers of most vehicles are prone to make right-hand turns, is this the case in all situations, most situations, or only some situations? If we view mathematic's as a type of vehicle being driven by billions of people (where different uses of numbers/mathematic's are represented by different types of vehicles from hand held cars to kiddy cars to racing cars, trucks, off-road vehicles, motorcycles, bicycles, etc...), are we to overlook the distinct usage of numerically referenced 1-wheeled vehicles (unicycles, wheelbarrows), 2-wheeled vehicles (bicycles/motorcycles/richshas/box-moving dollys, roller cabinets, etc...), 3-wheeled vehicles (tricycles, 3-wheelers, etc...), 4-wheeled vehicles (most motor vehicles/farm tractors/skates, skateboards, etc...), "5-wheeled" vehicles (5th wheel, steering wheel), 6-wheeled vehicles (buses, semi-truck tractors), etc..., and those vehicles with multiple, but a limited array of wheels (Tractor and trailer semi-trucks...18 wheelers..., tanks... multiple wheels encased in chain tracks, half-tracks, machinery, mechanical watches, etc...)?
While the different types of vehicles (mathematics/counting) have differentiated utility, the different applications need not be used to obscure basic patterns such as stop/go, up/down, from here to there, inside/outside. In other words, the complexity to which we humans apply mathematics to different configurations of underlying simple patterns need not obscure that a lack of progress is being made in the usage of the types of basic patterns. Mathematics is not moving humanity ahead despite all the external types of makes and models that are being fabricated and sold as a "new math":. We most often describe a vehicles power in terms of horse power. An old idea adapted to a different setting which helped the public find a meaningful comparison between flesh and bone (horse) transportation and mechanized transportation. Mathematicians use a similar tactic to sale the idea for the necessity of using mathematics, whereby no one is looking to step beyond this type of thinking to envision a new model which can transport human abilities into a new age. Similarly, Nature itself is not redesigning itself. It still uses the old tool called evolution, and its triplet-code pattern in DNA/RNA appears to be exempt from Evolution expressed in what could be counted such as a quadruplet, quintuplet, sextuplet, etc... codon system. Like politicians erecting laws which permit them to either circumvent them by claiming a specialized "National Security" provision, structure them with some loophole to take advantage of, or have some other stay-out-of-jail card such as a diplomatic immunity, both Nature and Mathematic's appear to work off of a similar premise of plausible deniability when things go wrong.
If we say that the recurring dichotomies to be found in mathematics is as natural as the pairing of amino acids is, does this automatically excuse mathematic's from likewise using this presumed natural order of processing as a reflection of an origin on a path towards obsolescence? Whereas a sail, oar, and life sustaining provisions accompanying you on a raft/boat in the middle of an ocean may provide comfort and hope of reaching some body of land, there is no guarantee that all will go well. Neither can the stable staples provided for by the underlying patterns in DNA and Mathematics... regardless of one's obsessional belief in such Natural provisions. If mathematic's is but an echo of Natural processes which come to change to the extent of creating an extinction of humanity, then the spider webs called human civilization (seen in the left-over monuments of past cultures), can well present any future being with a sticky mess of distraction, such as sentimental advocacies of claimed historical value.
Granted there are incremental changes in one subject area or activity from some former representation, but most often what we see is merely a swapping of placements, practices, and (typically)... people involved. Add to this that human individual and collective memory can be very short indeed, we are presented with a situation that it is frequently difficult for some people to recognize either a repetition or advancement. Change by way of simple substitution is sometimes described as a change (for the better or worse); even while the change does not in fact represent an advancement... however one might come to define what is meant by an advancement other than the mere adoption of one or more substitutions. Take for example the case in which one person replaces another as a political leader. While some may claim this as an advancement, the advancement in this case may mean little more than getting rid of corruption, and not that the underlying form of government has actually been altered to prevent any future corruption by one or more leaders from ever being elected to office again.
The same sort of changes can take place in any academic field. In the present case of examining Mathematics, we are confronted with a situation which I am claiming to be representative of a field that has reached a cognitive limitation due to an underlying repetition of a basic structure which is preventing it from advancing except by way of substitution. There is no new field of mathematics which has been developed to significantly alter the life framework of humanity. Mathematics, like all other genres of intellectual pursuit, has reached an impasse and is currently spinning it wheels... though the current drivers of the subject are too focused looking out their windshields to take a look sideways or rearward. It is like a circle of trucks bogged down a muddied ravine who can't actually see in front of themselves because the windshields are muddied by others attempting to race ahead in hopes of discovering some hitherto unexplored realm where some golden fleece, golden chalice or other golden opportunity awaits those who are willing to make not only the necessary amount of sacrifices, but the correct ones as well.
While different analogies exist to be used in the present essay, the present one will suffice as a means of introducing a recurring dependence by current mathematical models, on what I perceive to be an over-reliance upon the usage of dichotomization— as is found in psychology as well, and has been referred to as a condition of Persistent Dichotomies. In order to understand what I am talking about, it is of need to realize there is a large presence of dichotomization in Mathematics. While some readers may already be aware of this, they may not have placed their observation into the context of an enlarged set of examples found in other genres of research. Let me first provide a few examples from Mathematics (Dualities in Mathematics), and then some from psychology, though dichotomies from other subjects might well be included. And it should be noted that the word "dichotomy" is being illustrated in the present context with a multiplicity of intellectual garments such as opposition, complimentary, complementary, juxtapositioning, etc., and in general, as a pattern-of-two that may alternatively be represented by various labels within the context of a given subject's adopted vernacular, such as for example, duality, duo, bilayer, dimer, bifurcation, bipolar, fork, twice, two, one and one, three minus one, biad, couple, handedness, radius, etc..., some of which may indirectly point to a "two" but only a single and/or multiplicity are conventionally expressed.
Dualities in Mathematics- add/subtract
- whole numbers/fractions
- real numbers/imaginary numbers
- positive/negative (a "neutral" is cognitively available for inclusion)
- geometric/non-geometric
- multiply/divide
- X axis/y axis
- greater than/less than (equal to is centralized position)
- subscript/superscript ("middlescript" exists but is not characteristically labeled)
- (integer but no "outeger" nor "midteger"?)
- probability/improbability
- possibility/impossibility
- finite/infinitesimal
- Constructive (standard-traditional) analysis/Non-standard analysis (one might use the word "destructive or dissective")
- decidability and undecidability (as part of the two incompleteness theorems found in a discussion on meta-logic; from which the notion that axioms present us with a mechanistic adherence to problem solving. "metalogic." Encyclopædia Britannica. Article by Hao Wang, Professor of Logic, Rockefeller University, New York City, 1967–91. Author of Logic, Computers and Sets and others. And Morton L. Schagrin, Professor of Philosophy, State University of New York College at Fredonia. Author of The Language of Logic.)
|
And let us not forget to include such well-known dualities as the Nature/Nurture controversy, the Chicken/Egg dilemma, inner space/outer space, Micro-/Macro, Black/White (raciality), rich/poor (upper/lower social classes), Major/Minor musical cords, singularity/multiplicity, slow/fast, in the red/in the black (accounting), forward/about face, etc... In fact, let us take any subject and we can find some representative expressions of two-based ideas illustrated with a given subject's working vernacular. And yes, it is fully recognized that there are other patterns but the point to be made is that there appear to be only certain patterns which repeat themselves in multiple subjects. If one creates a makeshift graph simply to introduce the idea without intending to provide any real representative occurrence, we can imaginatively design a graph for the purposes of a philosophical conversation piece, which quickly advances to the notion we may be dealing with a diagrammatic puzzle akin to a Hamiltonian circuit occurring in three dimensions instead of a singularity, that a simple illustration such as the following is a simplistic beginning of a path similarly reviewed in other puzzles such as the three wells and the 7 bridges ideas.
Date of Origination: 19th March 2022... 5:23 AM
Initial Posting: 24th March 2022... 3:24 AM
Updated Posting: 2nd January 2023... 10:58 AM