~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
But Linnaeus was not satisfied with this "sexual system" of classification:
Classification by "natural characters"
Linnaeus did not consider the sexual system to be his main contribution toward the "reformation of botany" to which he aspired. His main contribution came in the form of a booklet, the Fundamenta Botanica (1736; "The Foundations of Botany"), that framed the principles and rules to be followed in the classification and naming of plants.
In 1735 Linnaeus met Hermann Boerhaave, who introduced Linnaeus to George Clifford, a local English merchant and banker who had close connections to the Dutch East India Company. Impressed by Linnaeus's knowledge, Clifford offered Linnaeus a position as curator of his botanical garden. Linnaeus accepted the Position and used this opportunity to expand certain chapters of the Fundamenta Botanica in separate publications: the Bibliotheca Botanica (1736; "The Library of Botany"); Critica Botanica (1737; "A Critique of Botany"), on botanical nomenclature; and Classes Plantarum (1738; "Classes of Plants"). He applied the theoretical framework laid down in these books in two further publications: Hortus Cliffortianus (1737), a catalogue of the species contained in Clifford's collection; and the Genera Plantarum (1737; "Genera of Plants"), which modified and updated definitions of plant genera first offered by Joseph Pitton de Tournefort.
Genera Plantarum was considered by Linnaeus to be his crowning taxonomic achievement. In contrast to earlier attempts by other botanists at generic definition, which proceeded by a set of arbitrary divisions, Genera Plantarum presented a system based on what Linnaeus called the "natural characters" of genera/morphological descriptions of all the parts of flower and fruit. In contrast to systems based on arbitrary divisions (including his own sexual system), a system based on natural characters could accommodate the growing number of new species often possessing different morphological features pouring into Europe from its oversea trading posts and colonies.
Linnaeus's distinction between artificial and natural classifications of organisms, however, raised the question of the mechanism that allowed organisms to fall into natural hierarchies. He could only answer this question with regard to species: species, according to Linnaeus, were similar in form because they derived from the same parental pair created by God at the beginning of the world. Many of his contemporaries shared a similar species concept. One such notable personage was French naturalist Georges-Louis Leclerc de Buffon, who was engaged in a similar all–encompassing natural history project at the time–though Buffon doubted the existence of natural genera, orders, or classes. Linnaeus tried to explain the existence of these divisions within the context of hybridization; however, the question of natural hierarchies would not receive a satisfying answer until English naturalist Charles Darwin explained similarity by common descent in his Origin of Species (1859).
Binomial Classification System
Linnaeus's most lasting achievement was the creation of binomial nomenclature, the system of formally classifying and naming organisms according to their genus (what general kind of life form) and species (which specific kind of life form). In contrast to earlier names that were made up of diagnostic phrases, binomial names (or "trivial" names as Linnaeus himself called them) conferred no prejudicial information about the plant species named. Rather, they served as labels by which a species could be universally addressed. This naming system was also implicitly hierarchical, as each species is classified within a genus. The first use of binomial nomenclature by Linnaeus occurred within the context of a small project in which students were asked to identify the plants consumed by different kinds of cattle. In this project, binomial names served as a type of shorthand for field observations. Despite the advantages of this naming system, binomial names were used consistently in print by Linnaeus only after the publication of the Species Plantarum (1753).
Linnaeus also sent a number of students on expeditions around the globe to collect exotic plants for acclimatization in Sweden. The most famous of these so-called "Linnaean apostles" include:
- Pehr Kalm, who traveled through North America between 1748 and 1751.
- Daniel Solander, who accompanied British explorer James Cook on his first circumnavigation (1768?71).
- Carl Peter Thunberg, who reached Japan in 1776.
Carolus Linnaeus article by: Staffan Müller-Wille, Research fellow, ESRC Research Centre for Genomics in Society, University of Exeter, England.
Let me also include a bit of history occurring in the article that might be overlooked as another binary type of influence. Like Einstein and many other researchers, Linnaeus had to find work to supplement his research interests and schooling. Let me provide some abbreviated references from the same foregoing article:
Because of his financial situation, he could only visit a few lectures; however, the university professor Olof Celsius provided Linnaeus access to his library. From 1730 to 1732 he was able to subsidize himself by teaching botany in the university garden of Uppsala. ...At this early stage, Linnaeus laid the groundwork for much of his later work in a series of manuscripts. Their publication, however, had to await more fortuitous circumstances.
In 1735 Linnaeus met Hermann Boerhaave, who introduced Linnaeus to George Clifford, a local English merchant and banker who had close connections to the Dutch East India Company.
While the article provides additional insight into the life of Linnaeus with respect to procuring positions to fund his interests, the latter entry in the ostensibly short review is to make mention that Linnaeus may well have had some knowledge of the new accounting system in the form of the double-entry method, which is based on a mathematical balancing act, where "both sides" of an equation (or accounts ledger) must balance out... even though a ledger may come to balance even when the wrong or bad accounts numbers are placed into the equation. A "fudging of numbers" can take place when a mistake is first noticed and yet the originating source either can not be identified or the accumulation of data (numbers) makes the task seem untenable, particularly under a time constraint situation that governments and business and religions like to instigate in an attempt to gain some advantage... particularly if they had a hand in creating a discrepancy. While there is a record of the double-entry system occurring in the 13th century, it was not until the 15th and 16th centuries that it appears to make its way into some publicized form. Supposedly, Luca Pacioli, a Franciscan Friar and collaborator of Leonardo da Vinci first codified the double-entry system in his mathematics textbook "Summa de arithmetica, geometria, proportioni et proportionalita" was published in 1494 Venice. However, there are other claimants to the title of who was first. (Double-entry bookkeeping)
The double-entry system is based on a (two-patterned mathematically based) Accounting Equation, seen in modern terms as:
The fundamental accounting equation, also called the balance sheet equation, represents the relationship between the assets, liabilities, and owner's equity of a person or business (Their worth, such as reputation). It is the foundation for the double-entry bookkeeping system. For each transaction, the total debits equal the total credits.

The typical basic equation is to add, subtract, multiply or divide one number in comparison to another number which results in a third number. This is similar to the logic structure of Major Premise (MP)- minor premise (mp>- conclusion. We can also equate the sequence of primary, secondary, tertiary to it. Other three-patterned sequences might well be further attributions as well as sequences which do not clearly show a three-pattern but imply it, such as in the case of RNA with a single strand and DNA with a double strand, yet no (as yet) existing dominant three-stranded configuration. Another example of an implied "three" sequence is the two- and three-germ layer models with no highly visible one-germ layer life form being universally described, though the sponges have been mentioned as such by some researchers. However, when we take all the 1- 2- 3 sequences into account, one might get the impression of an early counting system being repeated by both human cognition and nature, or nature imposed on humans (since humans are a facet of nature as well), or human cognition is imposing itself on Nature... whereby we have several structures exhibiting a triple formula.
However, simply adding, subtracting, multiplying and dividing a comparison of two numbers (or defined values (such as in the philosophical case of Father- Son/Sun- Spirit (Holy or otherwise), does not actually mean an actual three-patterned sequence has occurred. While the result is the third value in this conceptualization, it is not a new item. For example, we have two pieces of fruit or vegetables or two animals. There is no actual third animal unless one occurs through birth or from outside the group. If one farmer gives another farmer a goat, there are two goats, but the second goat given to the 2nd farmer is not a new goat, it is one that already existed, even if the farmer thinks the goat being received is interpreted as a reward or good fortune to be attributed to luck, a god, or some notion of shrewd business dealing. Such ideas are part of an ancient era in which a magico-religious model of thinking was dominant. If the farmer truly got the goat because it "all of a sudden" (poof/shazam/abracadabra) occurred, one might refer to the receipt of the goat as an unnatural occurrence or irrational/artificial (non-natural) increase in number/quantity. While the goat might be interpreted as a propitious (positive) "sign", others with a penchant for the superstitions might think of it (in negative terms) as an omen or portent of ill-tidings, so as to rain on the parade of the farmer. (Some people simply do not like to see another person prosper.)
As fanciful as the foregoing might seem to some readers, the point is we have a mathematics whose ideas are contours of very old ideas thrust into modern settings by way of altered labels and era-specific contextual applications which make them appear to be feasible. Many ideas used in Mathematics are "conjured up" artefacts of very ancient notions because Mathematics is an environmental setting which permits them to occur, albeit making sure the crude cave men and women (ancient notions) our outfitted with proper attire... much like making sure the town drunk is wearing an unsoiled suit and tie along with combed hair, shiny teeth, mouth-washed breath, and the appropriate social vernacular in order to enter a place of drunken revelry no longer called an orgy or in later times (metaphorically speaking) a whore house, saloon, bar, restaurant, etc., where in each successive case some measure of cleaning up the actions of patrons has taken place. The old notion of "anything goes" is taking place in Mathematics where the "house rules" are called axioms. So long as you abide by the house rules, you can do as you want. And if you don't like this type of establishment, you need only to develop your own set of axioms for those whose interests are inclined towards another way of thinking. Thus, if one develops a (twelve... preferably 10 or less) series of axioms involving some mathematically defined intellectual pursuit, they are to be included as part of the flock because it is advantageous for the Main sect of Mathematicians not to exclude a growing flock of (previously defined) Pagan practicing idealists. It is better to incorporate the outlying practitioners of a different mathematics craft into one's fold, and not ostracize them or a rift might ensue, causing some to question the reality of the two-patterned (Janus-faced) ideology that foundation of Mathematics rests on.
Like an imposing religion, Mathematics is everywhere. Instead of the obsessive-compulsive types of greeting that Moslems have, we have a society in which some mathematical signature is to be expressed, most often in forms that one might interpret as openly expressed secret passwords. Certain groups practice certain expressions with lengths and emphasis that can easily be converted to formulaic enumeration, and is a facility that the human mind is adept at doing much like an experienced trades-person with an abacus. The human mind is quite facile at converting perceptions of nature and social circumstances into a mathematical count or increasingly complex formula (typically simple arithmetical measurements). While most often not openly articulated, the mental process of humans can engage in a series of computations so as to result in variations of situational impressions describing:
- It adds up.
- It doesn't add up.
- That's equal, fair, even.
- That's not fair, equal, or half.
- How do you figure that?
- That figures.
- If you do this, you get that (consequences).
- If you fail to do it, you will not earn anything.
- What's up man? Not much. (A three-word phrase followed by a two-word phrase.)
- Another day, another dollar.
- Get rid of that! (In order to be left with a more desirable result.)
- How much... (does it cost)?
- How many are going?
- Are the right (number of) people going to be there?
- The crowd is big, large... a bunch of people. ("Many"). Though we seldom say a heap, hill, bushel of people.
- etc...
Mathematics, such as simple enumeration, can be found in linguistic utterances. In fact, if analyzed, one can apply enumeration to all things, though the patterns being observed and rendered into enumeration (or some applied formula) may not make sense since the numbers and/or formula do not conform to a conventional rationale being socially practiced. While one may be paying witness to a better formula of logic, the logic may not appear as a standard perception until society works its way through its presently practiced formulas of nonsense created by businesses, governments and religions. Such institutions are sustaining an atmosphere in which a two-patterned Mathematics model is permitted to thrive and flourish, whereby a systemic practice of symbiotic relationships are perpetuated. By altering the basic formula from a two- to a three-model, just as we humans are striving to do by creating a quantum computer, the entire civilization of humanity will eventually be transformed, though pockets of two-patterned thinking individuals will claim their way of thinking is more natural... closer to Nature.
The duality nature of Mathematics is problematic because it references a stagnation which pretends to take a step forward, like the previously mentioned farmer who was excited about receiving a second goat, and yet the entire village in which the two farmers existed did not gain another ' goat. The farmers were thinking from the perspective of a singular frame of mind involving a world perspective in which the two farmers were the dominant focus; just like many a parent are so over-bearing so that they alone are the singular focus everyone should have. However, Mathematics takes into account the reality of duality and attempts to append it to an appreciation of itself in linguistic circumstances:
In mathematics, (duality is a) principle whereby one true statement can be obtained from another by merely interchanging two words. It is a property belonging to the branch of algebra known as lattice theory, which is involved with the concepts of order and structure common to different mathematical systems. A mathematical structure is called a lattice if it can be ordered in a specified way (see order, such as the perspective of architectural columnar order). Projective geometry, set theory, and symbolic logic are examples of systems with underlying lattice structures, and therefore also have principles of duality.
Projective geometry has a lattice structure that can be seen by ordering the points, lines, and planes by the inclusion relation. In the projective geometry of the plane, the words “point” and “line” can be interchanged, giving for example the dual statements: "Two points determine a line" and "Two lines determine a point." This last statement, sometimes false in Euclidean geometry, is always true in projective geometry because the axioms do not allow for parallel lines. Sometimes the language of a statement must be modified in order that the corresponding dual statement be clear; the dual of the statement "Two lines intersect in a point" is vague, while the dual of "Two lines determine a point" is clear. Even the statement "Two points intersect in a line," however, can be understood if a point is considered as a set (or "pencil") containing all the lines on which it lies, a concept itself dual to the idea of a line being considered as the set of all points that lie on it.
There is a corresponding duality in three-dimensional projective geometry between points and planes. Here, the line is its own dual, because it is determined by either two points or two planes.
In set theory, the relations "contained in" and "contains" can be interchanged, with the union becoming the intersection and vice-versa. In this case, the original structure remains unchanged, so it is called self-dual.
In symbolic logic there is a similar self-duality if "implied" and "is implied by" are interchanged, along with the logical connectives "and” and "or."
Duality, a pervasive property of algebraic structures, holds that two operations or concepts are interchangeable, all results holding in one formulation also holding in the other, the dual formulation. ("duality." Encyclopædia Britannica.)
Not only is duality pervasive in Algebra, but the whole of Mathematics. It is a Westernized model of the Yin-Yang system of thinking. So much so is the pervasiveness, we see it cropping up in supposed scientific experiments such as in the case of the perceived dual nature of particles sometimes referred to as a "wavicle," resulting from a two-patterned structured idea involving "two slits" through which light was passed, as described by the double-slit experiment carried out by Thomas Young in 1801.
The observation of interference effects definitively indicates the presence of overlapping waves. Thomas Young postulated that light is a wave and is subject to the superposition principle; his great experimental achievement was to demonstrate the constructive and destructive interference of light (c. 1801). In a modern version of Young's experiment, differing in its essentials only in the source of light, a laser equally illuminates two parallel slits in an otherwise opaque surface. The light passing through the two slits is observed on a distant screen, as shown in the figure. When the widths of the slits are significantly greater than the wavelength of the light, the rules of geometrical optics hold—the light casts two shadows, and there are two illuminated regions on the screen. However, as the slits are narrowed in width, the light diffracts into the geometrical shadow, and the light waves overlap on the screen. (Diffraction is itself caused by the wave nature of light, being another example of an interference effect.) The superposition principle determines the resulting intensity pattern on the illuminated screen. Constructive interference occurs whenever the difference in paths from the two slits to a point on the screen equals an integral number of wavelengths (0, ƛ, 2ƛ,...). This path difference guarantees that crests from the two waves arrive simultaneously. Destructive interference arises from path differences that equal a half-integral number of wavelengths (ƛ/2, 3ƛ/2,...). Young used geometrical arguments to show that the superposition of the two waves results in a series of equally spaced bands, or fringes, of high intensity, corresponding to regions of constructive interference, separated by dark regions of complete destructive interference.
("light." Encyclopædia Britannica.) Excerpt of a larger article by: Glen Stark, Professor of Physics, Wellesley College, Massachusetts, U.S.
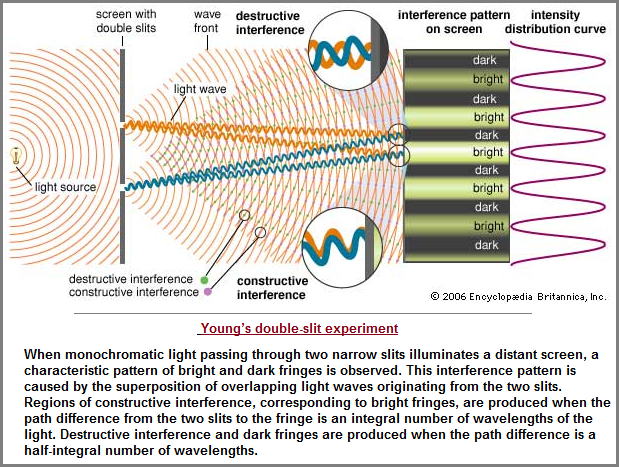
If the reader would think back about my mention of the I-Ching triads involving solid and split lines, with the split lines referring to the yin (female) principle and the solid line referring to the yang (male) principle; one might see the two slits set against or on a solid board as representative of two yins and one yang, or one male with two females. Then again, one might see the third line in a "True Trigram" being illustrated. While the sexual connotation may lead some to think in terms of promiscuity or some family relationship (Father- Mother- Child) or other triadic scenario, the point is the experiment was conducted much in the style of the old dual Chinese format. Indeed, this is problematic for all concerned with the replication of ancient ideas onto modern efforts seeking to evolve beyond such conceptualizations frequently acting as intellectual anchors in waters which may not be continually viable due to environmental changes. And I should mention that in an earlier rendition of the double-slit experiment image, I referenced the two slits as eyes (acknowledged here as missing a third "middle" eye, configured in insects as ocelli set into a triangular array much like the usage of three satellites for GPS triangulation and global communications systems).
If we rely upon a dual perspective to see the world, necessarily so we need tools (such as Mathematics) and experimental evidence (such as the foregoing double-slit idea) to confirm our inclinations. However, when we come upon a situation which appears to support a dominant three-patterned characterization such as that seen in particle physics or the three germ layers in biology, there may be an unacknowledged and unrealized inclination to focus on two-patterned forms and formulas, attesting to the possibility that the human brain/mind is not adequately developed to live in a world with a dominant three-patterned perspective because too many existing institutions support a dualistic orientation such as seen in religion, politics and business.
If the wave/particle duality is a reality and not something created by the human mind, and other two-patterned structures are likewise real, we must account for the "2" in contrast to a "3" and other patterns, and thus need to seek out a model which will best help us to grasp what we are involved with, at least in a numerical sense. While I have pursued a serial number model to account for what appears to be a series of repeating patterns mostly oriented in a small assortment of small number representations along with a few large number out-lyers, one or more other models might prove to be serviceable as the environmental situation continues to deteriorate, and humanity has neither the intelligence nor technology to effectively confront to bring about a different outcome. In my model of enumeration which appears to represent a counting sequence labeled as occasions of simple to more complex developments, I am left with presently noting that there appears to be a limitation as to how much real complexity can be achieved. While one might want to describe acts of multiplication as revealing complexity in terms of organism development, let us not that mere doubling of cells does not in itself lead to an "emergent property" of complexity in terms of what we might describe as an evolutionary gain. For example, there are multiple life forms which develop from multiplications of dividing sex cells, yet they do not achieve a sentience which we humans described as a "higher" intelligence. Yet, when we come to differentiate life forms with three germ layers as opposed to two, the usage of such does not itself arise in the development of more intelligence, just that which is coincidental with a given species. Therefore, having three germ layers is not the definitively singular process to account for more complexity in terms of a human model of brain activity, whether the reader describes it as good "or" bad or good "and" bad or good "not" bad/ reversed as bad "not" good, as one might characterize the Boolean forms of choices.
(continued on next page)
Date of Origination: 19th March 2022... 5:23 AM
Initial Posting: 8th August 2022, 9:10 AM
Updated Posting: 2nd January 2023... 10:56 AM