~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
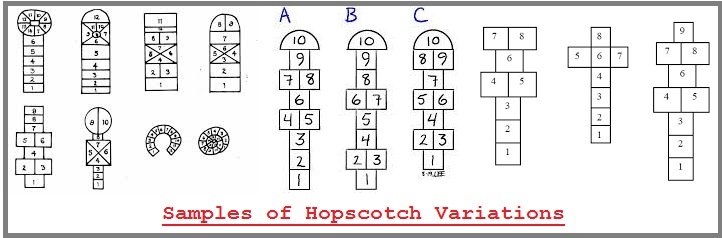
As mentioned, another example of this increased complexity is seen in the game of hopscotch, which apparently has variations in "many" countries according to the following article, though only a small assortment of examples is provided. Nonetheless, the idea created by adults which describe some games as having a universal application of practice while others do not, is a point about a cognitive standard which needs to be investigated. (However, with respect to games with lines defining behavioral conduct, one might include baseball, basketball, bowling, football, track-n-field, shuffle-board, miniature golf, etc...).
(Hopscotch is an) age-old children's game based on an idea of not treading on lines. Variations of the game are played in many countries. The game's English name expresses its object: to hop over the "scotch," a line, or scratch, drawn on the ground. Lines are drawn in a variety of patterns. Spaces in the diagrams are numbered, and they must be traversed in order.
Whether we think of the items being used to mark one's position in a game such as hopscotch as remnants of a more ancient activity of using sticks and pebbles, lines in the dirt, or some other instrument (rocks, shells, beads, bones, leaves, fruit, etc...) assisting us in calculating our position with regards to some enumerative value; let us not fail to recognize we are involved in some rudimentary counting behavior that by today's standards of labeling might be termed set theory. A one-to-one correspondence is another way of saying the word "pair" and using one or more additional numbers in or out of a group is a related reference associated with a set, and thus participates as a member of the set like a person who prefers to remain at the outskirts of a social gathering, be it a family, party, celebration or other gathering (funeral, wedding, birthday party, meal time, etc...). In any respect, we are brought to the topic of "Relations in set theory", of which the following Britannica excerpt is representative:
In mathematics, a relation is an association between, or property of, various objects. Relations can be represented by sets of ordered pairs (a, b) where a bears a relation to b. Sets of ordered pairs are commonly used to represent relations depicted on charts and graphs, on which, for example, calendar years may be paired with automobile production figures, weeks with stock market averages, and days with average temperatures.
A function f can be regarded as a relation between each object x in its domain and the value f(x). A function f is a relation with a special property, however: each x is related by f to one and only one y. That is, two ordered pairs (x, y) and (x, z) in f imply that y = z.
A one-to-one correspondence between sets A and B is similarly a pairing of each object in A with one and only one object in B, with the dual property that each object in B has been thereby paired with one and only one object in A. For example, if A = {x, z, w} and B = {4, 3, 9}, a one-to-one correspondence can be obtained by pairing x with 4, z with 3, and w with 9. This pairing can be represented by the set {(x, 4), (z, 3), (w, 9)} of ordered pairs.
Many relations display identifiable properties. For example, in the relation "is the same colour as," each object bears the relation to itself as well as to some other objects. Such relations are said to be reflexive. The ordering relation "less than or equal to" (symbolized by £) is reflexive, but "less than" (symbolized by <) is not. The relation "is parallel to" (symbolized by ∥) has the property that, if an object bears the relation to a second object, then the second also bears that relation to the first. Relations with this property are said to be symmetric. (Note that the ordering relation is not symmetric.) These examples also have the property that whenever one object bears the relation to a second, which further bears the relation to a third, then the first bears that relation to the third–e.g., if a < b and b < c, then a < c. Such relations are said to be transitive.
Relations that have all three of these properties—reflexivity, symmetry, and transitivity—are called equivalence relations. In an equivalence relation, all elements related to a particular element, say a, are also related to each other, and they form what is called the equivalence class of a. For example, the equivalence class of a line for the relation "is parallel to" consists of the set of all lines parallel to it.
Robert R. Stoll, Professor of Mathematics, Cleveland State University, Ohio, 1971–80. Author of Set Theory and Logic; Herbert Enderton, Professor of Mathematics, University of California at Los Angeles. Author of A Mathematical Introduction to Logic; Elements of Set Theory; and others.
The repeating patterns to be found in Mathematics is conducive to being examined as part of a "set theory" of cognitive activity, that I have elsewhere referred to as a "standard cognitive model". Some sets such as patterns-of-two and patterns-of-three, appear to occur more often then other sets in some settings. while there are a variety of sets, the overall count of the sets being used appears to be limited... or let us say conserved. Mathematics seems to be rather inclined to use patterns-of-two which is similar to the patterns-of-two sets found in the yin and yang compilation of two-patterned sets examples. Some sets, such as the idea of three families of fundamental particles can be viewed as a Natural phenomena or Natural set occurring in particle physics, or we might otherwise entertain the notion that in the context of particle physics the professionals in the field are cognitively inclined to reduce information to such a pattern... for whatever reason one might want to argue for or against such a view. The same situation exists for the dominating idea of a triple code in DNA and that humans are on the third planet.
Nature itself, in terms of biology, might be said to be inclined towards the usage of two-patterned sets being reduplicated like an infant babbling repeated two-patterned consonant/vowel "chunks" such as Ba-Ba-Ba, Na-Na-Na, Ti-Ti-Ti, Da-Da-Da, etc... The individual pairings, like individual words, may be expressed singularly, or in a multiple fashion that may be termed nonsense sentences or nonsense expressions, only because we so-called intelligent adults have no idea what is actually being expressed by such sounds or the precursor-to-babbling utterances call vegetative sounds. I say Biology is appeared to be inclined to using sets-of-two as seen in the doubling process of cell division, the use of a double-helix, as well as a bilateral symmetry approach to the development of multiple organisms. However, in some instances, there is no doubling of chromosome pairs and there is a uniform chromosome number of 108:
Equisetopsida: (division Pteridophyta, is a), class of primitive spore-bearing vascular plants. Most members of the group are extinct and known only from their fossilized remains. The sole living genus, Equisetum, order Equisetales, is made up of 15 species of very ancient herbaceous plants, the horsetails and scouring rushes. Extinct members of the division, some of which have been traced back as far as the Devonian Period (416 to 359 million years ago), include many herbaceous Equisetales, shrubby Hyeniales, vinelike Sphenophyllales, and trees of the family Calamitaceae.
Certain Equisetopsida flourished as trees (e.g., Calamites species) during the coal-forming Carboniferous Period, but the earliest sphenophytes appeared as early as the Devonian. In its fossil history the class constituted a much larger portion of the flora of the Earth than it does at the present time.
Equisetum, which may also have been present during the Carboniferous, is perhaps one of the oldest living genera of vascular plants. The more primitive species have perennial, green shoots. The advanced species have annual, green, branched, vegetative shoots and often non-green, unbranched, fertile shoots. Intermediate combinations of these features occur in some species.
Chromosome numbers in Equisetum are uniformly x = 108. Several hybrids are known, but all are sterile as there is no doubling of the chromosome number to allow chromosome pairing and consequent production of viable spores. ("Equisetopsida." Encyclopædia Britannica.)
In Biology we also find the notion of duplication as a type of pairing occurring in a set with respect to the following senses:
Heterozygous duplication (an extra copy of some chromosome region) also results in a genomic imbalance with deleterious consequences. Small duplications within a gene can arise spontaneously. Larger duplications can be caused by crossovers following asymmetrical chromosome pairing or by meiotic irregularities resulting from other types of altered chromosome structures. If a duplication becomes homozygous, it can provide the organism with an opportunity to acquire new genetic functions through mutations within the duplicate copy.
If a chromosome break occurs in each of two non-homologous chromosomes and the two breaks rejoin in a new arrangement, the new segment is called a translocation. A cell bearing a heterozygous translocation has a full set of genes and will be viable unless one of the breaks causes damage within a gene or if there is a position effect on gene function. However, once again the pairing properties of the chromosomes at meiosis result in aberrant meiotic products. Specifically, half of the products are deleted for one of the chromosome regions that changed positions and half of the products are duplicated for the other. These duplications and deletions usually result in inviolability, so translocation heterozygotes are generally semi-sterile ("half-sterile").
An individual with additional chromosome sets is called a polyploid. Individuals with three sets of chromosomes (triploids, 3n) or four sets of chromosomes (tetraploids, 4n) are polyploid derivatives of the basic diploid (2n) constitution. Polyploids with odd numbers of sets (e.g., triploids) are sterile, because homologous chromosomes pair only two by two, and the extra chromosome moves randomly to a cell pole, resulting in highly unbalanced, nonfunctional meiotic products. It is for this reason that triploid watermelons are seedless. However, polyploids with even numbers of chromosome sets can be fertile if orderly two-by-two chromosome pairing occurs.
Though two organisms from closely related species frequently hybridize, the chromosomes of the fusing partners are different enough that the two sets do not pair at meiosis, resulting in sterile offspring. However, if by chance the number of chromosome sets in the hybrid accidentally duplicates, a pairing partner for each chromosome will be produced, and the hybrid will be fertile. These chromosomally doubled hybrids are called allotetraploids. Bread wheat, which is hexaploid (6n) due to several natural spontaneous hybridizations, is an example of an allotetraploid. Some polyploid plants are able to produce seeds through an asexual type of reproduction called apomixis; in such cases, all progeny are identical to the parent. Polyploidy does arise spontaneously in humans, but all polyploids either abort in utero or die shortly after birth. ("heredity." Encyclopædia Britannica.)
Returning to the idea of set theory as practiced by Mathematicians and using biology as a basis by which an analogy related to cognitive activity has parallel structuring, multiplicity occurring in biological development can be equated with the Mathematical notion of "Axioms for compounding sets:"
Although the axiom schema of separation has a constructive quality, further means of constructing sets from existing sets must be introduced if some of the desirable features of Cantorian set theory are to be established. Three axioms in the (following) table—axiom of pairing, axiom of union, and axiom of power set—are of this sort. ("set theory." Encyclopædia Britannica.)

In short, set theory exists in every subject one might care to entertain, if they can accustom themselves to the use of a adaptive generalization involving the presence of different objects as correlational attributions within groupings that may have a variety of labels consistent with the language of a given subject. More simply put, items and ideas of different subjects can be viewed as groupings, such as those seen in particle physics, crystallography, family groups, genetics, chemistry, etc... Beyond this simple realization is that certain groupings appear to occur more often than others in given subjects, and this may then be related to cognitive processing.
With respect to psychology and pairing, not only do we see the persistent use of dichotomies (such as Nature/Nurture, Bipolarism, sanity/insanity, etc...), but also have the notion of "twin maddess" described by the French phrase of "folie a deux," defined in the WordWeb dictionary as "The simultaneous occurrence of symptoms of a mental disorder (as delusions) in two persons who are closely related (as siblings or man and wife)." No less, the general term "disorder" might be use in some instances to describe either a lack of pairing or an unequal pairing, if not an over-abundance of a given quality/quantity which creates either a welcomed or unwelcomed occurrence.
While mathematics, Biology, Astronomy, Physics, Art, Music and the like are major identities of ideas, they make up only a few sets or altogether make up one set. Divisions of study within the Major indices can be viewed as subsets or functions of the main topics. The point is that after w remove all the subsets, all the divisions within a major category of study, we have only a limited quantity and quality. But this is understood and not difficult to contemplate. Another way of saying it is that we have a handful of Major fields of study and multiple genres of exploration beneath them, if such a featured sentence is needed for others to grasp what I am saying about limitation, without attempting to belabor the point. This matter because it is typical for all sub-divisions tend to use the same type of underlying patterns that the parent uses, and thus we might be inclined to discard them so as not to duplicate the findings of what kinds of patterns, of what kinds of sets we uncover in the parental heading. Though some sub-discipline may well focus on some other pattern that the parent label does not, just like some singular organism in a list of multiple creatures in a given terrain, this does not mean the pattern of one creature, one sub-discipline... necessarily alters the count of the dominant set in the larger dominant group.
Mathematically we might create a (Capital Letter) A through Z or (Natural Number) 1 through 26 set of letters or numbers resulting in 13 pairs of each, or a combined 26 pairs. A subset of the Capital Letter group could be designated as small letters and a subset of the Natural Number group might be viewed as fractions. However, we find that Natural Numbers are themselves a subset of real numbers which involves ideas such as fractions, Positive and Negative, as well as rational and irrational... or otherwise noted as frequent sets of dichotomous pairs being used as a foundational philosophy which governs the development of rules called axioms...used as a guideline by which a given way of thinking about a certain topic is to be viewed, much like a board or other game accompanied by instructions... though without such instructions people might well create their own, altering them so as to reduce the chance of conflicts or appearance of unfairness. In this sense, if Mathematics used its axioms to analyze itself, it would find discrepancies in it assumptions. One of which is the over-riding usage of patterns-of-two that is reminiscent of a fixed game from which is populated a skew of results in a given direction of thought that social customs have come to mimic and define as the proper requirement of that called mathematically-aligned logic.
If we say all groupings can be viewed as symbolic forms of mathematical sets, then the Yin/Yang compilation is a type of basic math expression. Let us look at one rendition of the Yin-Yang idea:
(yin-yang) Wade-Giles romanization: yin-yang, Japanese in-yo
In Eastern thought, the two complementary forces that make up all aspects and phenomena of life.
- Yin is a symbol of earth, femaleness, darkness, passivity, and absorption. It is present in even numbers, in valleys and streams, and is represented by the tiger, the colour orange, and a broken line (representing the vagina).
- Yang is conceived of as heaven, maleness, light, activity, and penetration. It is present in odd numbers, in mountains, and is represented by the dragon, the colour azure, and an unbroken line (representing the penis).
The two are both said to proceed from the Great Ultimate (taiji), their interplay on one another (as one increases the other decreases) being a description of the actual process of the universe and all that is in it. In harmony, the two are depicted as the light and dark halves of a circle.
The concept of yin-yang is associated in Chinese thought with the idea of the Five Phases (wuxing)—metal, wood, water, fire, and earth—both of these ideas lending substance to the characteristically Chinese belief in a cyclical theory of becoming and dissolution and an interdependence between the world of nature and human events.
The origins of the yin-yang idea are obscure but ancient. In the 3rd century BCE in China, it formed the basis of an entire school of cosmology (the Yin-yang school), whose main representative was Zou Yan. The significance of yin-yang through the centuries has permeated every aspect of Chinese thought, influencing astrology, divination, medicine, art, and government. The concept entered Japan in early times as in-yo. A government bureau existed in Japan as early as 675 CE to advise the government on divination and on control of the calendar according to in-yo principles, but it later fell into disuse. In-yo notions permeated every level of Japanese society and persist even into modern times, as evident in the widespread belief in lucky and unlucky days and directions and in consideration of the zodiac signs when arranging marriages. ("yin-yang." Encyclopædia Britannica.)
If we claim the over-riding usage of patterns-of-two in Mathematics suggests a connection with the yin-yang idea or some assumed fundament representation of Nature, the problem with this comes in the form of references of Nature which do not abide by the usage of patterns-of-two, such as DNA's triplet code, the fact that the Earth is the third and not the second planet and that in particle physics we find three families. Not to mention seven colors to the color spectrum, three dimensions of space and one assumed time dimension, as well as three laws of motion, three laws of planetary motion; most people apparently using three fingers and not two to hold a pen or pencil as well as three trimesters to pregnancy, to name but a thimble-full of examples. If "two" was so important one would think it would be pervasive, but it isn't. There are other "natural" patterns but that overall, there are only a few patterns being repeated.
However, is Nature using a simple pairing method for everything? A pairing method that we may later call symmetry if it involves a one-to-one correspondence, but call it asymmetrical if it involves structures which are odd-numbered, odd-shaped, or provides some other characteristic we may or may not articulate as "oddness", but nonetheless react to it with some unacknowledged (or unnamed) aversion which represents a non-categorized type of symmetry because there exists an overall ensemble of three types of "symmetry-aligned orientation" to the effect we have the grouping: Symmetry- Non-Symmetrical- odd-Symmetry, and Bilateralism is a separate entity, even though we attach the word symmetry to it and will say "Bilateral symmetry" because there is an unspoken inclination in science to use "threeism" for many researchers while others prefer a "twoism" and some a "sevenism" or otherwise?
Is Nature "stuck" in a mode of expression that we may define as a simplistic counting method? Just because humans assert that an organism is complex, doesn't make it so. If we take a dollar and double it and then double the outcome of each result for 90 days (the general length of time for a human pregnancy type of organism/baby) development, do we conclude the doubling effect is a complexity, even if we were to allocate a certain number of funds into three separate categories called germ layers (banking accounts), with further allocations into different sectors (physiological sections such as teeth, organs, skin, etc...)? Is it really a complexity or only because some humans in the past defined it as such and later generations simply mimicked such perceptions? If we say it is not complexity we might otherwise describe it as a multiplicity of pairing events like a computer code to which is initially applied the boolean triangle of And- Not- Or (gates..., much like a three germ layer divisioning). Theses of course have been later added (divided) on to with additional orientations. Retrospectively, they are channels of switching or queuing, just like Germ layers which remind me of a train depot, bus station, airport and ship port, though several other types of analogies might be used to define points at which any number of directions might be taken, but that an itinerary is being exercised to define the path... even if it is the behavior of following clues or searching for clues to some sought after treasure.
While reading the following excerpts, one can not but chuckle at how similar the references are to what is taking place on a biological context related to the Germ Layer situation:
Queuing Theory
(Queuing Theory is a) subject in operations research that deals with the problem of providing adequate but economical service facilities involving unpredictable numbers and times or similar sequences. In queuing theory the term customers is used, whether referring to people or things, in correlating such variables as how customers arrive, how service meets their requirements, average service time and extent of variations, and idle time. When such variables are identified for both customers and facilities, choices can be made on the basis of economic advantage.
Queuing theory is a product of mathematical research that grew largely out of the need to determine the optimum amount of telephone switching equipment required to serve a given area and population. Installation of more than the optimum requires excessive capital investment, while less than optimum means excessive delays in service. ("queuing theory." Encyclopædia Britannica.)
Switching Theory
Theory of circuits made up of ideal digital devices, including their structure, behaviour, and design. It incorporates Boolean logic (see Boolean algebra), a basic component of modern digital switching systems. Switching is essential to telephone, telegraph, data processing, and other technologies in which it is necessary to make rapid decisions about routing information. ("switching theory." Encyclopædia Britannica.)
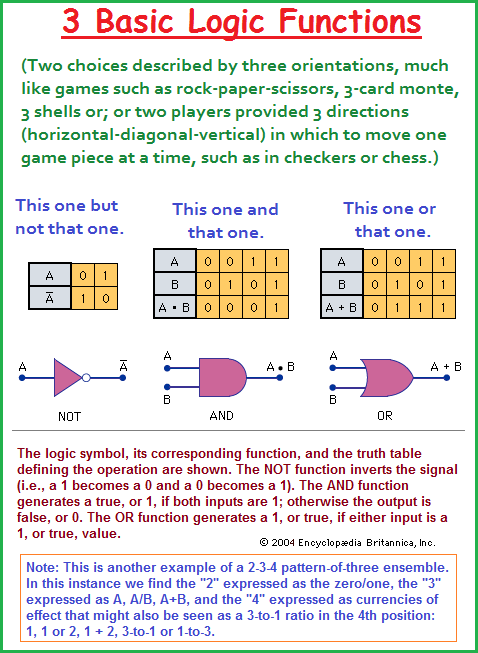
With the introduction of switching, queuing and boolean logic (Boolean Algebra), there is a need to reference the pairing of Alternating Current (AC) with Direct Current (DC), as well as Analog and Digital circuitry involving series and parallel circuits. One can not help but notice the to-be-made correlation between the truth tables of boolean logic and the 2-3-4 logic used to describe the logic of which value is appropriate for establishing the rule that there is a triplet code and not a dual nor quad. In other words, a dual code is too small and a quad code is too large because the former (dual) has too few amino acids to include the 20+ essential amino acids and latter (quad) has too many. The "truth table" of amino acids results in a 3 X 4 configuration or a 4 X 4 X 4 = 64, to be additionally correlated with the 64 squares found on both checker and chess boards. In other words, there is an underlying recurrence of a cognitive pattern(s) resurfacing, but the cognitive pattern(s) is/are conserved. There are only a few being repeated.
Analog versus digital circuits
Analog, or linear, circuits typically use only a few components and are thus some of the simplest types of ICs. Generally, analog circuits are connected to devices that collect signals from the environment or send signals back to the environment. For example, a microphone converts fluctuating vocal sounds into an electrical signal of varying voltage. An analog circuit then modifies the signal in some useful way—such as amplifying it or filtering it of undesirable noise. Such a signal might then be fed back to a loudspeaker, which would reproduce the tones originally picked up by the microphone. Another typical use for an analog circuit is to control some device in response to continual changes in the environment. For example, a temperature sensor sends a varying signal to a thermostat, which can be programmed to turn an air conditioner, heater, or oven on and off once the signal has reached a certain value.
A digital circuit, on the other hand, is designed to accept only voltages of specific given values. A circuit that uses only two states is known as a binary circuit. Circuit design with binary quantities, “on” and “off” representing 1 and 0 (i.e., true and false), uses the logic of Boolean algebra. The three basic logic functions—NOT, AND, and OR—together with their truth tables are given in the figure. (Arithmetic is also performed in the binary number system employing Boolean algebra.) These basic elements are combined in the design of ICs for digital computers and associated devices to perform the desired functions. ("integrated circuit (IC)." Encyclopædia Britannica.)
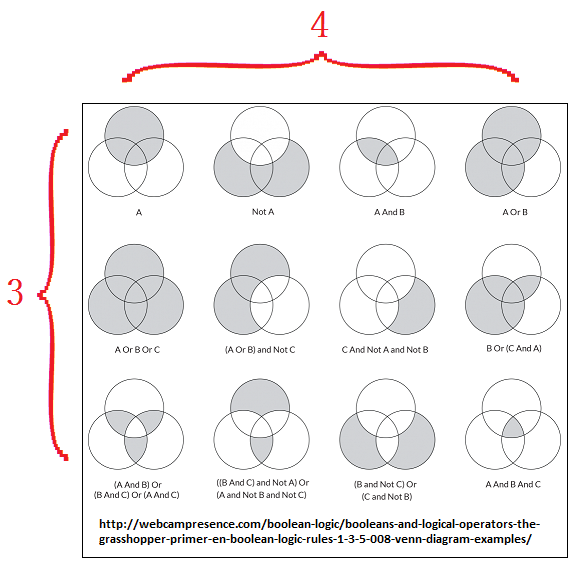
The three "Not- And- Or" gates (doors, directions, paths, trails, etc...) can take on a multiplicity of partialized choices as seen in the following Venn diagrams, but one must note once again we are being presented with an overall limitation. Please note the 3 X 4 paneling arrangement and compare this with the illustration of both amino acids as well as the "3 X 4 cubicle" idea found in particle physics:

The self-inductance of a circuit is used to describe the reaction of the circuit to a changing current in the circuit, while the mutual inductance with \ respect to a second circuit describes the reaction to a changing current in the second circuit. ("electromagnetism." Encyclopædia Britannica.)
By viewing the basic (numerically identifiable) patterns in different subjects, one can contrast these ideas with those which take place in mathematics. The recurring presence of such patterns has produced a system of structure where there either exists an emerging language and/or we can align such patterns to represent characteristics of already established languages, and thus construct some measure of a meaningful expression. I do not know if it is an old... ancient language the human mind was born with (like a reflex or instinct) and has struggled to find a means of expression, or it is a new language suggesting an evolutionary development of encephalization, whereby the usage of "quantitative alignments" (we humans label as "counting", or a sense of number, or enumeration) by different life forms are additional representative examples that something is occurring in different measures across all, some, or a few phenotypical genotypes.
Whereas we can be sure that humans are expressing themselves in recurring patterns in different subject areas much differently than they expressed themselves in earlier historical orientations for which we have a record for, though we can not read all written records (some better than others); we do not know whether the so-called quantity assortment (counting) behavior of different (non-human) life forms, is a new or old phenomena. Then again, are some life forms expressing a "counting" behavior in a more sophisticated way than that to be interpreted by way of the techniques humans are using as measurement tools? In any respect, the non-human life forms are not using what we describe as language or mathematics, therefore it is more difficult to discern whether there is a means to understand basic cognitive patterns of humans other than by establishing some criteria for developing a language which can accurately describe the recurring patterns being exhibited in different subjects by way of assigned numbers to different subject matter? Then again, how much of what is being said by the mind or brain is being accurately described, or does the mind/brain simply adapt to the environmental setting it is cast into, whereby whatever forms of expression are available (music, art, science, letters, words, numbers, symbols, sounds, etc...), this is the medium of expression to be used and contorted in an attempt by a person to find a more clearer representation of what the brain is doing in response to the environment, sometimes referred to as the ultimate truth, the ultimate essence, the purest note, a sacred law, a pristine image, etc.?
If Mathematics is the "queen" of all sciences, this is the same as claiming it as an ultimate truth, as an inviolable reality. Yet, if Mathematics itself is but one of several models of expressing some underlying language, it is of need to look at it as a crude vernacular. Perhaps a form of stuttering, system of clicks, babbling, or other primivity. When we can not look upon mathematics as but another type of brain activity trying to superimpose itself on other mental activities as if it is a life form seeking to parasitize itself so as to ensure survival... or simply as an organism born with a different survival strategy, then we are not ready to consider that the potential for finding a greater truth, a greater realization, a greater developmental path already exists within us, if we would only permit it to be exercised and not constrain it by forcing all mental activity to kow-tow to present models of mathematics, because mathematics is itself in an immature stage of development.
In voicing the opinion that it is possible to establish a new model of Mathematics phrased as an "Accordian Mathematics" and claiming it is dynamic while the present model of Mathematics is static, this entails the realization that I am speaking towards the perspective that present Mathematics is not evolving, but instead in an exercise circularity of repeating itself as a species that has become a dead end in evolutionary terms. A dynamic Mathematics points to the availability of being able to pursue growth towards a greater lineage, but that such a potentiality can not be realized until humanity comes to terms with being able to recognize the present state of Mathematical toolage is akin to a conveyor belt system of stone-age tools that some have become quite adept at using, but it is equivalent to a horse and saddle means of intellectually exploring different terrains. While it remains an excellent choice by which to navigate rough terrains of intellectual endeavour, we can not allow such a roughage to be written into socially required laws of how humanity not only should live, but must live in order to perpetuate such a model of Mathematics as a Natural and Nationalized (or Inter-Nationalized) Preserve. We can not continue to pursue the adoption of educational standards which restricts the human mind from developing beyond the current overall crude model of mental activity we call Mathematics, and likewise wants to enforce all forms of commerce and social standards to abide by the dictates of patterns being carved out by such crude tools and persuasively force Legislators and all social leaderships (in all industries and orientations) to make the entire structure of society, its laws, its spirituality, its hopes, its dreams and its triad concept of heart- mind- soul, to be fashioned in its image.
Mathematics, like art and music; are the three recurring activities being seen as exercised by savants (both social and solitary models) who often display prodigious memories, can help us to recognize what we can initially describe as an emergent language, (Though the "emergence" may only be the act of realization of its existence, in that it has always existed in some form but humans were not wholly cognizant of it and it may be the case the human brain was not developed enough either to express it or become aware of it). Because all subjects are expressing some model of what we believe to be a basic structure, it is this basic structure we need to come to identify and allow to mature as a viable language of underlying mental activity trying to swim to the surface from depths which may be at the beginning of biology itself, as a medium by which an extra-terrestrial message had been planted. However, when I say "message", I am merely referring to the presence of a repeating pattern and not that something is being conveyed to whatever life form reaches a stage of development in order to grasp whatever significance can be culled out of the patterns.
(continued on next page)
Page Series origination: March 22, 2022, 6:57 AM
Initial Posting: 8th August 2022, 9:10 AM
Updated Posting: 2nd January 2023... 10:46 AM