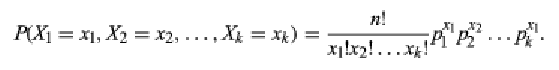~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
Many people harbor some sense of feeling that there is something more to life than that currently being experienced or practiced by humanity, and that it is obtainable if one could only find the means of achieving it... and is realized by those thinking to take advantage of the phenomena whereby they create a philosophy, religion or some alternative direction along some defined practicality which uses the labor of others to achieve the substitute idea. Various labels (conveyed here in English) as Heaven, Nirvana, Paradise, Shrangri-la, Higher Consciousness, Higher plane of existence, Transcendence, Utopia, political power, financial position, career position, Olympic gold (medal), Academic achievement, Nobel prize (various socially prestigious awards exist), Champion, No. 1, Chosen people, Chosen land, etc., speak of something... a presumed some 'place', some existence exists (if even for a moment to encapsulate into a life-long illusion or delusion of grandeur) beyond the assumed veil of presently practiced consciousness, which others try to exploit with some proposed means of achieving such a state of existence; only to eventually find themselves having been taken advantage of, or having to create some illusion... if not a delusion or full-blown psychosis as a retreat from a reality they want to escape; because something gnaws at them in indistinct methods and manners.
While some exhort to adopting a simpler way of life to achieve what they think is a clearer picture of some assumed existing reality, others turn to various forms of intoxication as if by this route they can achieve some semblance of a higher state of being... of existence— by altering their brain chemistry so as to unlock synaptic firings among brain neurons that are thought to be blocked, detoured or enslaved by the routinization of thoughts mimicking the ideas of an established way of life (created by self-serving governments, businesses, religions)p for which the person comes to perceive as little more than a tread mill set into a hamster, rat or other life form encasement (colloquially called a cage) which they routinely describe as a prison or limitation. This is how I see Mathematics, and indeed, all present forms of adopted ideology— though there are those who are quite adept at using them as fully functional tools which assists them in acquiring a better living standard for themselves and their family, if not friends, relatives, acquaintances, and others. Yet, not all people who are adept at art, science, mathematics, philosophy, physics, languages, music, baking, chemistry, body building, acting, singing, instrument playing, automotive mechanics, carpentry, Astronomy, Anthropology, teaching, etc., are able to apply their skills sufficiently enough to acquires some "upper" realm of socially acceptable economic sufficiency. Needless to say, having a college degree is not magic wand. Luck, personality, weight, height, gender, race, religion, era into which one is born, one's language(s) facility, age, interests, diet, extra-curricular activities, narrowness of mind/focus, patriotic/political/sexual orientations, etc. etc., can all have an impact.
Mathematics has achieved some measure of universal usage, and therefore can be more easily recognized as being similar to an organism which has successfully spread into different habitats and achieved viability. Yet, we do not likewise view it as a possible virus, parasite, or other invasive species. Many people do not use a broad form of comparison amongst different subjects in order to entertain the ideas found in one subject area may be occurring in one or more others albeit disguised in labels and forms/formulas which assist in creating a camouflage. Many people do not see recurring patterns though they use them every single day. Many people do not reduce perceptions to numbers or equations or poetry to songs, or songs to a linguistic analysis, or the multiple other types of analogies different people use on a daily basis, though most often restricted to one or a few topics. If Mathematics itself can not be visually discerned as acting like a life form, then human usage thereof is unconsciously using it as if it were a type of beast-of-burden, slave and indentured servant which has created a vast operational network of dependency.
By using a biological model applied to Mathematics, it is a routine to decipher activity into its underlying patterns, many of which are described with numbers. In multiple other instances, words are used that can likewise be interpreted as quantitative expressions, though in most cases biological models are not taken to the next step of enumerated exploration involving more complex number valuations such as we find in simple mathematical operations. Instead, complexities are imagined in singular instances which have become elaborated by some preoccupied results garnered from experimentation. Longitudinal studies can be "complexified". Examples of words or phrases being used to express number or quantity have already been stated, but let me reintroduce the idea for those readers whose habit is to "glean" a page and fall upon a sentence or paragraph somewhere other than at the beginning of some page. Here are a thimble-full of examples from different perspectives:
- Singularity = "one" which equals "1".
- Monad = "one" which equals "1".
- Universe = "one" which equals "1".
- Mono = "one" which equals "1".
- An unscripted molecule such as H (for Hydrogen) = "one" which equals "1".
- Primary (often) = "one" which equals "1", but could be used to describe more than one.
- Dyad, Di-, dual, dichotomy, pair, binary, biad, one- and- one (correspondence), etc. = "two" which equals "2".
- Secondary = "two" which equals "2".
- Triad, Tri-, triad, trinity, triune, triplicity, ternary/trinary, etc., = "three" which equals "3".
- Tertiary = "three" which equals "3".
- Much, Many, More, Heap, a lot, few, etc., can sometimes refer to three (3) or three and more, or more than three without including three.
- Quaternary can refer to someone's notion of four (4), but can also be used as an alternative representation of much, many, more, etc., which is equivalent to three (3), or is equivalent to a 3-to-1 ratio, where the word "to" is not meant to be restrictive to other considerations such as with, for, and, or; or some other conjugation such as may be illustrated in a numerical sense of notation where a comma follows each grouping of three numbers
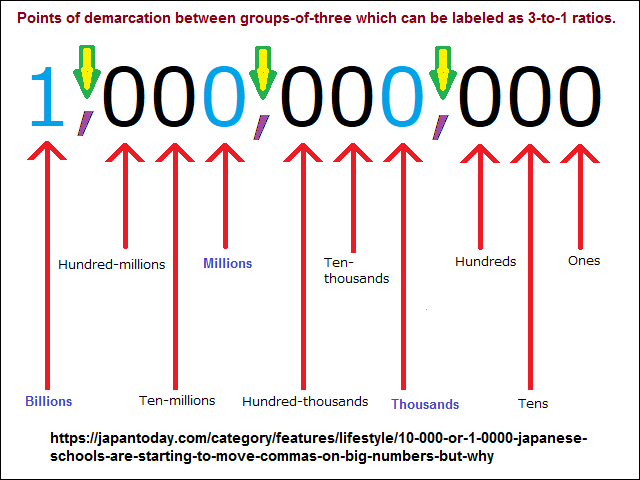
The place values notation reflects a recurring pattern of cognitive activity seen in other subjects. Sometimes the three is portrayed as a singularity, though it may be alternatively described in relation to one or more other values with a mix and match of color, sound, symbol, gesture or incidental physiological response. The values can be reversed and be replaced by other variables, whereby no distinct "3" or "1" is suspended long enough for a given consciousness to appropriately analyze or label. Again, here is a reference list of various 3-to-1 compilations: Three to One ratios page A. The point to make is that it is a recurrence of thought which provides for a different direction of thought that using a label of "four" does not provide. Using the value of "4" is an expression of sequentiality which plays into the hands of those who have conventionalized mathematics into a route form of thinking and in particular, how to think about thinking and thought processing. It is a conventionality seen in the idea of Persistent Dichotomies used not only in the field of psychology, but mathematics as well as computer language in terms of a binary which some are trying to supersede with a trinary (or ternary) code, and we see lingering in the concept of a Binomial Nomenclature for Biology.
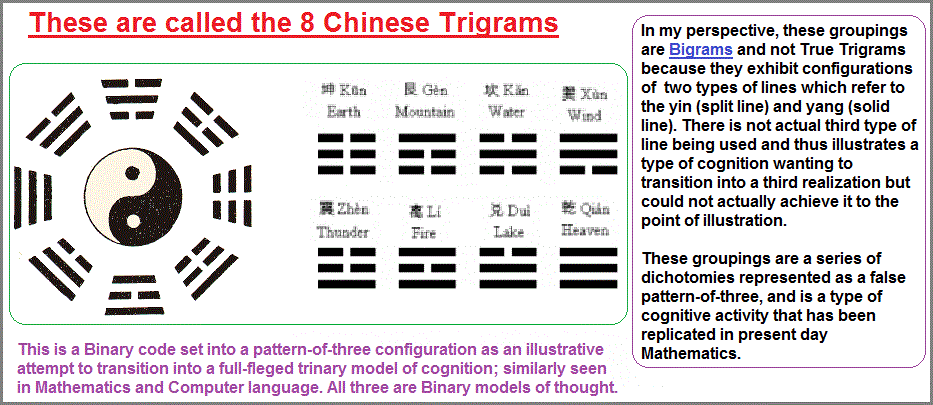
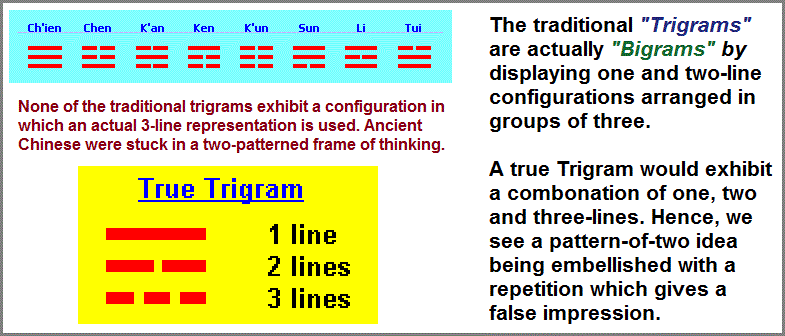
However, the use of a binomial or pattern-of-two formula should not automatically be viewed as an invaluable tool. Where there is a currency of recurring two-ness, there is no fault in using a pattern-of-two as a means of listing information. The fault lies in thinking that it is an appropriate one-size-fits-all model which takes upon itself some imagined propriety of authoritative value assigned with the labels of tradition, sacredness, convention, routine, etc., whereby no other approach is used to examine or categorize observations. In some instances, the use of twos is valuable, because the material being examined does indeed exhibit "two-ness", but that this should not prevent attempts to see or arrange information alternatively. For example, the many dichotomies of Mathematics have become established as a useful tool, but this usefulness as been translated into not only an expectation but a resolute propriety of preventing an alternative model of mathematics being proposed by way of a realization that present mathematics is itself a type of anciently practiced Binomial system of thinking about reality. In effect, it is a different model of the yin/yang perspective with a predominant two-patterned orientation which later came to adopt a trinary and octinary formula by way of three-lined system of 8 concepts called the eight triads, though I call them Biads, because there us no separate three types of lines used, only two forms representing male (solid line) and female (split line) configurations. Mathematics, like the Yin/Yang concept are old ideas by those whose perceptions of reality can be reduced to a binomial theorem overlayed with an octave triadic system. (One of the octaves is seen in chemistry known as the octet rule). Here is an excerpt from the Britannica about the Yijing, (In some respects, Mathematics too is used for divination):
Chinese "Classic of Changes" or "Book of Changes" Wade-Giles romanization: I-Ching or Yi-Ching, also called Zhou Yi
An ancient Chinese text, one of the Five Classics (Wujing) of Confucianism. The main body of the work, traditionally attributed to Wenwang (flourished 12th century BC), contains a discussion of the divinatory system used by the Zhou dynasty wizards. A supplementary section of "commentaries" is believed to be the work of authors of the Warring States period (475–221 BC) and, as a philosophical exposition, represents an attempt to explain the world and its ethical principles, applying a largely dialectic method. For this the work came to have great importance in the history of Chinese philosophy. Modern scholars, nevertheless, have been troubled by the inclusion of the Yijing among the Confucian classics, for Confucius (551–479 BC) seems to have deliberately avoided speaking of anything that suggested esoteric doctrines. The answer seems to be that Han dynasty Confucianists (c. 2nd century BC), influenced by the Daoist quest for immortality, justified their use of the Yijing by attributing certain of its commentaries to Confucius.
Though the book was originally used for divination, its influence on Chinese minds and its universal popularity are due to a cosmology that involves humans and nature in a single system. The uniqueness of the Yijing consists in its presentation of 64 symbolic hexagrams that, if properly understood and interpreted, are said to contain profound meanings applicable to daily life. Throughout the ages, Yijing enthusiasts have claimed that the book is a means of understanding, and even controlling, future events.
The Yijing hexagrams are formed by joining in pairs, one above the other, eight basic trigrams (bagua). Each trigram has a name, a root meaning, and a symbolic meaning. The legendary emperor Fuxi is said to have discovered these trigrams on the back of a tortoise. Wenwang is generally credited with having formed the hexagrams.
In practice, one "creates" a hexagram by casting lots in one of several ways. The hexagram is built up from the bottom, line by line, by successive lots. Solid lines have the number nine, and broken lines have the number six. Solid lines represent yang (the male cosmic principle), while broken lines represent yin (the female cosmic principle). These two principles explain all being and all change by their ceaseless interaction.
Individual lines of a hexagram have been compared to single notes of music. Though each note has a quality and significance in itself, its truest significance depends on its place in a musical score. Because the same principle applies to individual lines of a hexagram, the Yijing text first explains each line separately, then gives an overall interpretation of the unit. The text is often expressed in cryptic, thought-provoking language, thus allowing the user great leeway in interpreting its significance. ("Yijing." Encyclopædia Britannica.)
A "hexagram" is another way of referencing the quantity of legs on insects:
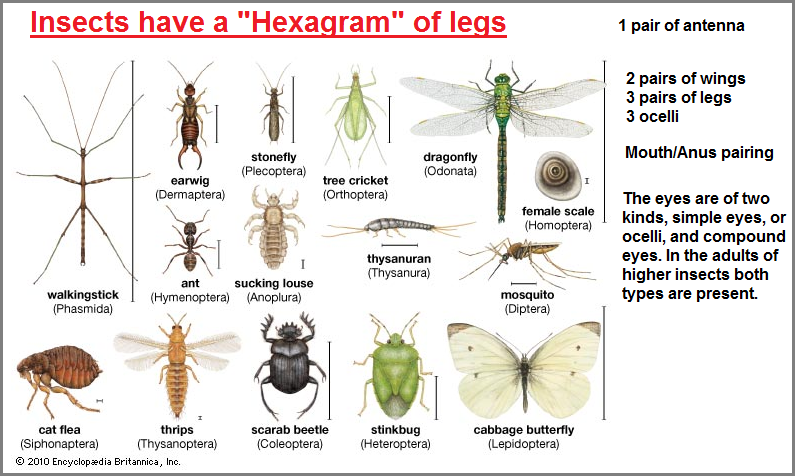

The usage of patterns-of-two in the Yin/Yang concept, Mathematics and Computer language is part of an unrecognized statistical probability occurring with human cognition, even though there exists the idea of Binomial distribution. The idea simply has not been applied to human cognitive activity because the set of tools being used by so-called experts have been romanticized by over-valuations due to personalized attachments, like someone with a favorite chair, favorite fishing pole, favorite wrench, favorite piece of clothing, favorite author, etc... by examining a definition of what is meant by Binomial distribution and then recognizing there is a second adopted view called Multinomial distribution, one might then see the underling expressions of a "two" (for Binomial) and "many" for Multinomial, and think of these in terms of a basic form of primitive counting. This counting formerly begins at a "two" since no single or mono-nomial distribution distinction is warranted and after the "two" or binomial distinction, the cognitive activity adopts a "many" approach as a generalize collectivity for all quantities beyond the "two". In other words, it is a one-two-many expression in the form of a (taken-for-granted mononomial)- Binomial- Multinomial sequence. Humorously, a Binomial Distribution can be viewed as a study of dichotomies yet does not see any conflict or bias in using a dichotomous mathematics tool of inquiry as posing any problem. HA! In fact, the usage of two die in the following example is another bit of biasness, since games of win/lose chance are thus compounded by the usage of die which render a win or loss, and most people don't see this as an irrationality!
(Binomial Distribution): In statistics, a common distribution function for discrete processes in which a fixed probability prevails for each independently generated value.
First studied in connection with games of pure chance, the binomial distribution is now widely used to analyze data in virtually every field of human inquiry. It applies to any fixed number (n) of repetitions of an independent process that produces a certain outcome with the same probability (p) on each repetition. For example, it provides a formula for the probability of obtaining 10 sixes in 50 rolls of a die. Swiss mathematician Jakob Bernoulli, in a proof published posthumously in 1713, determined that the probability of k such outcomes in n repetitions is equal to the kth term (where k starts with 0) in the expansion of the binomial expression (p + q)n, where q = 1 - p. (Hence the name binomial distribution.) In the example of the die, the probability of turning up any number on each roll is 1 out of 6 (the number of faces on the die). The probability of turning up 10 sixes in 50 rolls, then, is equal to the 10th term (starting with the 0th term) in the expansion of (5/6 + 1/6)50, or 0.115586. For further mathematical detail, including an explicit formula for the kth term of a binomial expansion, (see binomial theorem).
In 1936 the British statistician Ronald Fisher used the binomial distribution to publish evidence of possible scientific chicanery—in the famous experiments on pea genetics reported by the Austrian botanist Gregor Mendel in 1866. Fisher observed that Mendel's laws of inheritance would dictate that the number of yellow peas in one of Mendel's experiments would have a binomial distribution with n = 8,023 and p = 3/4, for an average of np ≅ 6,017 yellow peas. Fisher found remarkable agreement between this number and Mendel's data, which showed 6,022 yellow peas out of 8,023. One would expect the number to be close, but a figure that close should occur only 1 in 10 times. Fisher found, moreover, that all seven results in Mendel's pea experiments were extremely close to the expected values—even in one instance where Mendel's calculations contained a minor error. Fisher's analysis sparked a lengthy controversy that remains unresolved to this day.
Article by Richard Routledge, Professor of statistics at Simon Fraser University, British Columbia, Canada.
One must wonder if the pea experiments were a way by which Mendel could express a binomial math exercise, where the exercise took place in his mind and was not committed to paper, as is the case for some savants, but "intermittent savantism" (intermittent genius, intermittent talent, intermittent creativity, intermittent wisdom, intermittent expertise, intermittent language facility, etc...) is not a routine topic of acknowledgement, since most people think that expressions of genius are due to a "full-time' disposition of someone being a genius (or really smart, or really creative, etc...), and not that such activities can occur sporadically depending on context because those who come to pay witness to a difference in thought or activity might be frightened by it and move away from those circumstances most conducive towards influencing a given person to be "unusual" or non-typical. Most people want to have an unusual or unique ability that conforms to some socially recognized uniqueness (typically involving art, music, mathematics/numbers... memorization). They want their peers or social group leaders (family, friends, colleagues, relatives) to recognize and favorably comment about their ability, which is admitting to the desire of conforming to a set value of biased option. One can have the potential for great wisdom, creativity, mental acuity, etc., but if it is a quality which is ahead of its time, they will most likely be lost to history, not even gaining a mention as a footnote or some marginalia mark. Very often if a person is not recognized for a given quality, someone else takes credit for their work, or their work is used to create a variation of the same idea which becomes publicized and those who come across it have no idea that another person initiated the direction of thought or activity. (And yes, I am speaking of personal experience with respect to information regarding threes research and that found at two Enyclopedia sites which neither mentions Michael Eck or myself.)
Let use look at a Britannica excerpt of Multinomial Distribution, keeping in mind we are witnessing the application of a duality to a presumed multiplicity, but nonetheless exhibits we are dealing with an expression of statistics when we map out the rather conserved distribution of cognitive patterns being repeated in all the different subject areas. As we include more and more examples of the same repeating cognitive patterns (expressed in numbers), there are only a thimble-full of patterns suggesting either humanity's brain processing is forced to accommodate a type of consistency in environmental stresses (which are nonetheless deteriorating), or humanity's brain has reached (or about to reach) its ultimate level of probability functioning within the environment to which it is subjected and must effectively adopt a practice of rationalization that best fits a presumed survival equilibrium.
(Multinomial distribution): In statistics, a generalization of the binomial distribution, which admits only two values (such as success and failure), to more than two values. Like the binomial distribution, the multinomial distribution is a distribution function for discrete processes in which fixed probabilities prevail for each independently generated value. Although processes involving multinomial distributions can be studied using the binomial distribution by focusing on one result of interest and combining all of the other results into one category (simplifying the distribution to two values), multinomial distributions are more useful when all of the results are of interest.
Multinomial distributions are common in biological and geological applications. For example, 19th-century Austrian botanist Gregor Mendel crossed two strains of peas, one with green and wrinkled seeds and one with yellow and smooth seeds, which produced strains with four different seeds: green and wrinkled, yellow and round, green and round, and yellow and wrinkled. His study of the resulting multinomial distribution led him to discover the basic principles of genetics.
In symbols, a multinomial distribution involves a process that has a set of k possible results (X1, X2, X3,..., Xk) with associated probabilities (p1, p2, p3,..., pk) such that ∑pi = 1. The sum of the probabilities must equal 1 because one of the results is sure to occur. Then for n repeated trials of the process, let xi indicate the number of times that the result Xi occurs, subject to the restraints that 0 ≲ xi ≲ n and ∑xi = n. With this notation, the joint probability density function is given by:
Article by: William L. Hosch, Editor, Encyclopædia Britannica.
Along with Binomial and Multinomial distribution ideas, the ideas of Binomial theorem, Poisson approximation, Central Limit theorem and Law of Large Numbers are mentioned in separate Britannica articles. Before providing the excerpt of the latter, let me note that when compiling a list of (enumerated) basic cognitive patterns from different subjects, there is some variability of a few large numbers, but most numbers appear to be centralized within the one, two, and three digit range, whether or not as a human exercise in condensation, such as for example describing pi with the three numbers "3.14" (otherwise known as Einstein's birthday), and those who are able to carry out the sequence to a few further points (though Daniel Tammet has taken the value to 22, 514 digits and holds the record). While such a feat as Daniel Tammet's is lauded as an expression of genius, the genius in his ability rests more so on the recognition that the human brain (at least in some instances) is able to perform beyond the ordinary, and is thought to have great value if we could learn how to create such a condition in others, thought the extremes of assertiveness or passivity i personality are an overlooked (or at least not socially commented on as an) attribute in most cases. In addition, we might also ask, so what? So what if one or a hundred or a billion people could recite enormous values for pi? What good is it other than to show a talent for such, and more broadly speaking, what good are seemingly gargantuan feats of memory or repetition as seen in artistic and musical acts? Why only a small assortment of activities we value highly as a human group (though individually there are others), and those activities exhibit an underlying pattern-of-two formula, such as we find in mathematics, music and art?
Are the numerically labeled patterns of cognitive activity a graphically plottable distribution that can provide us with a statistical probability of what should be or will be a currency of cognitive activity, if not also tell us that the present cognitive behavior values are skewed along a direction of discernible deterioration? For example, let us say we have the most values of cognitive activity occurring in single digit references (- through 9), a lesser distribution in double-digits, and afterwards find there are diminishing references with respect to three, four, five, etc... digits numbers. If ideas in physics is exhibiting a dominant usage of two- and three-patterned organizations, can we use this as a primary reference base or must we use some other subject's enumerated cognitive valuations? Will we be able to see which subjects don't incorporate a given value, not because they don't exist, but because of the pool of researchers and/or researchers in a given field are caught up in a culture whose vernacular emphasized ideas are skewed due to former dominating ideas? Let me introduce a hypothetical graph concerning number distributions related to cognitive activity in multiple subjects. Not all subjects will necessarily have the same values distributions, and some will likely have some number values more than others. The graph also doesn't include other multiple (more than two) digit examples nor provide for wide variances which may not be found elsewhere except in a given instance. It also does not give an account of closeness such as those examples as the Speed of light being rounded up (or down) to the nearest larger value. In such an example instead of referring to the Speed of light as 299,792,458 meters per second, or 186,000 miles per hours, or 983,571,056 feet per second, we might say 300,000 kilometers per second. As another example of rounding up, we might say the temperature of outer space is "about" (the single digit) 3 degrees kelvin, while others would prefer to use three digits and describe it as 2.73 degrees. The use of a particular value may involve whether a person prefers to use one or two or three (or more) digits, because they are using the value more as a projection of a quality about themselves or a statement of acceptable "generality" when the exact figure is not known.
In the idea concerning a "Law of Large Numbers," we must decide whether to view recurring patterns as randomly generated variables, variables which are made up to coincide with a particular era's social orientation, or a "randomness" due to an unrecognized "randominity" of the material being examined. For example, are the expressions of different hominids and overall lineage, the product of a randomness that some describe is how life came into existence... that is, by chance and not by any intention or specifically directed result? Are the cognitive patterns "we" are seeing in different subjects due to a cognitive randomness that we might otherwise describe as a ramblingness? Has humanity been engaged in a cognitive activity akin to a gypsy which has extended for hundreds if not thousands of years? Are the recurring patterns of cognitive activity which we can list today merely the expression of a given time period in the overall history of humanity due to an unrealized physiological state? The idea that a value approaches some valued "1" reminds me of those who seek to condense everything to coincide with the concept of a singular god, as an extension of their egotist personality, routinely seen in many sports events where fans and players may refer to themselves in a fashionable sense of being "No. 1"... the best, the champions... as an ultimate achievement of personalized effort, vicariously acquired or not.
In statistics, the (Law of Large Numbers is a) theorem that, as the number of identically distributed, randomly generated variables increases, their sample mean (average) approaches their theoretical mean.

The law of large numbers was first proved by the Swiss mathematician Jakob Bernoulli in 1713. He and his contemporaries were developing a formal probability theory with a view toward analyzing games of chance. Bernoulli envisaged an endless sequence of repetitions of a game of pure chance with only two outcomes, a win or a loss. Labeling the probability of a win p, Bernoulli considered the fraction of times that such a game would be won in a large number of repetitions. It was commonly believed that this fraction should eventually be close to p. This is what Bernoulli proved in a precise manner by showing that, as the number of repetitions increases indefinitely, the probability of this fraction being within any pre-specified distance from p approaches 1.
There is also a more general version of the law of large numbers for averages, proved more than a century later by the Russian mathematician Pafnuty Chebyshev.
The law of large numbers is closely related to what is commonly called the law of averages. In coin tossing, the law of large numbers stipulates that the fraction of heads will eventually be close to 1/2. Hence, if the first 10 tosses produce only 3 heads, it seems that some mystical force must somehow increase the probability of a head, producing a return of the fraction of heads to its ultimate limit of 1/2. Yet the law of large numbers requires no such mystical force. Indeed, the fraction of heads can take a very long time to approach 1/2(see figure). For example, to obtain a 95 percent probability that the fraction of heads falls between 0.47 and 0.53, the number of tosses must exceed 1,000. In other words, after 1,000 tosses, an initial shortfall of only 3 heads out of 10 tosses is swamped by results of the remaining 990 tosses.
"law of large numbers" Article by: Richard Routledge, Professor of statistics at Simon Fraser University, British Columbia, Canada.
As structured, Mathematics can be claimed to be an overall exercise in attempting to achieve some sort of repeatable average by being applied to numerous instances. Instead of applying a two-based Yin/Yang orientation, Western minds created a two-based Mathematics. Like two-based, or let us say two- germ layered organisms which thrive and are useful the current model of life existing on Earth, and a two-based computer system, Mathematics is useful but can only take us so far. We can see the... let us say... "deficiencies" of a two-based (binary-coded) computer system and a two-based germ layer structure, so too must we view Mathematics in a similar light. While humans may want to claim that the Double-stranded DNA has a triplet code, this perspective may be an indication of the human mind striving for some semblance of a stature beyond a "two", like primitive forms of counting which upon reaching a conscious recognition of "2" initially used a third word such as "many" or heap, or pile, or bunch, etc... The idea of a triplet code may be an expression of humanity striving for a "greater number", or if true in a real sense and not as a projection of some cognitive search for a greater consciousness; then the triplet code may be a means by which life itself is seeking a greater enumeration beyond a two-based developmental scenario, just as humans are striving to go beyond a two-based (binary) coding system in computers by developing a trinary (ternary) platform. A sort of three-germ layer model from which complexity can arise.
Just as life went from a usage of a two- germ layer configuration to three layers, and we humans are striving to produce a triplet computer code model distinct from the present binary body plan used in computer language, so too must we develop a model of mathematics with a triplet platform differing from its present dichotomous orientation. Such an orientation is not without structures which advance some greater value, like bilateral organisms which come to possess "more-than-two" parts and functionalities, and a binary computer code upon which is applied a triple Boolean logic system; we can find more than dichotomies being used in some developed branches of Mathematics. Mathematics has its multiple life form branches, but they too have not yet evolved into using a basic structure commensurate with the advent of a triple germ layer ensemble. Then again, the current Mathematics model, let us call it a life form or creature, may be incapable of transcending its self to a "higher plane of existence", and must therefore be replaced with a different model of Mathematics which has the ability to do so, and that is what I am labeling as Accordian Calculus.
The analogies between Mathematics, Computer language and Biology can easily be seen by some readers. They may have recognized the two and three structures themselves and made some mental note of the patterns both individually and collectively, but not thought of it in the manner I am proposing, though there may be some that have but have not committed such ideas to a written form, or at least any written form for public consumption, unless there is a similar idea having been or about to be published in some Language other than English or in a manner that only a few are privy to reading because so many excellent ideas are being held ransom behind pay walls or "club membership" requiring some modernized form of a secret handshake, password, or other signification of being an accepted member.
For some readers, more information in the way of evidence is needed before they are convinced. Unfortunately, some will never be convinced and will go to their graves believing Mathematics is Queen of all Academic subjects because they have eventually come to use it for advice in an attempt to better themselves. In presenting a picture of why we need a new model of mathematics, it should be understood that the present model is useful and there are those who are quite adept at using it, but that its structure is a foreign language to most people. They can understand simple arithmetic but go no further. This is frequently interpreted to mean either a person can't think logically enough (colloquially referred to as being less smart), or that Mathematics itself is of a crude nature the (assumed) advancing human mind is reacting to it as an archeological artifact. Some think it's cool, strange, bizarre, weird, funny looking, beautiful, interesting, nice, viewed as a game, as a toy, or even ask what's it used for or what good is it in a person's day-to-day life. There are many reactions to Mathematics, but most often we think that a person simply needs to be trained in using its language by developing certain feats of memorization and visual manipulation.
Yet, if we describe Mathematics as a tool requiring the use of an ancient cognitive system of thinking in dualities, and that the modern mind is configured more so towards a usage of triples, we then have the case for re-examining mathematics as an artefact just like the yin/yank model of thinking. Just because the dichotomous nature of mathematics is concealed in a "foreign" language of symbols and signs requiring a cryptic exercise of breaking codes sometimes used by those in the past so as to conceal their ideas from different authorities or potential (real or imagined) antagonists; doesn't make Mathematics a "must-have" skill nor that it should be interpreted as a highly advanced ancient script to be cherished as an National (international) treasure. No matter what language, if everyone knew the same language... this does not guarantee humanity would be better off. The same goes for the idea if all humans shared the same race, or gender, or job skills, or sexual orientation, or religion, music, etc... The present state of humanity is clearly similar to life forms whose existence is marked by a development with two germ layers. Like organisms which have a bilateral structure, but whose parts are used functionally different when interacting with the same type of environment, so too do we find humans exhibiting this character. If we say that a use of Mathematics distinguishes some measure of mental development along a given parameter of orientation, let us further recognize it as a branch of development which affords us with a limited success of further survival.
(continued on next page)
Date of Origination: 19th March 2022... 5:23 AM
Initial Posting: 8th August 2022, 9:10 AM
Updated Posting: 2nd January 2023... 10:47 AM