~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
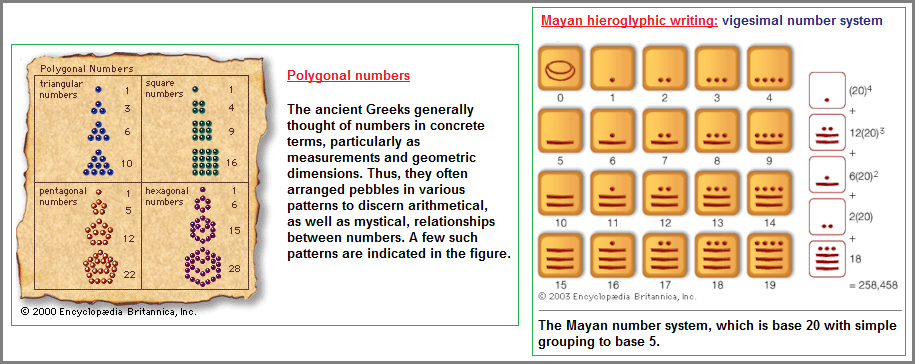
In as much as there were cultures experimenting with numbers (congruent with era-specific symbology) and a variety of pseudo-scientific orientations seeking a universal truth from which could be derived a knowledge providing formidableness (a formidability) against perceived enemies and hardships; many civilizations later came to develop a formula of Mathematics (inquiry, formulation, practical applications) with a versatility to be indulged by many different social interests, be it alchemy/Chemistry; astrology/Astronomy; philosophy + metaphysics/Physics; herbal remedies/Medicine; Biology (cultivation, animal husbandry, fishing...); prognostication/Meteorology; construction/Architecture; Psychology + counseling (palmistry, divination, augury, old soul wisdom, seerage); etc... However, many of the internalized culturations (such as those that came to be labeled as sects, secret societies, cults, etc...), retained esoteric specializations of number, geometry and symbolism which represented personalized ideas of conviction that at times proved be contentious statements about reality for which there was no established proof, and partitioners of such ideas were quite persuasive for others to adopt their pseudo-mathematical orientations because of the lack of mathematical tools need for refutation. Hence, Mathematics leaned more-so towards establishing itself not only with practical applications, but required of itself a means of attempting a system of substantiation and proofing, much like the rigor eventually applied to all perspectives indulging in the use of the word "Science". With the adoption of ideas called axioms purporting to represent a step-wise systematic logic for the use of mathematical formulas, the way was paved for the then unwitting development of an analogically-derived model of mechanistic thinking, much like logistics being applied to a terrain one is attempting to survey and traverse into uncharted territories of visualized contours which may intermittently bubble up in one's consciousness.

However, I view the present state of Mathematics as an exercise of primitive patterns primarily being used to create interesting tapestries and kaleidoscopic arrays of thought displayed in locations similar to placing rugs on walls, along halls, entrance ways, and as wallet size laminated inscriptions, informational mouse pads, beverage doilies, textbook footnotes and marginalia, refrigerator mantled to-do lists, napkinized doodlings, etc... In this respect, if I may use the vernacular of those who build vehicles to be displayed at car shows, the final creation of the project is viewed as being "All Show, No Go". In other words, while the constructed idea (formulaic displays of mathematics) is nice to look at, it has no internal capability of great (horse-power torque) performance aptitude sometimes referred to as muscle, from which the notion of "muscle cars" arises, though often colloquially viewed solely in terms of speed measured in proscribed drag-strip or race-track lengths. Despite those who might want to argue otherwise because they take the analogy in a literal sense and as a personal affront to their own mathematical interest, abilities and application thereof; in my view Mathematics is static, not dynamic... not evolving. (It is akin to a vehicle sitting on blocks in a salvage yard awaiting to be stripped for other uses then its initial formulated intent.) Biologically speaking, it is like viewing an ocean of different life forms which are profuse in regeneration of the same multiple types of organisms, but none have evolved to the point they begin moving onto land, much less taking flight like a soaring reptilian (pterosaurs and pterodactyloids) or some later creature called by the generic term of 'bird'. While present forms are in ways hybrids and some were a "next-stage" evolutionary outcrop, mathematics as a singularly defined creature has stopped evolving. Instead, the versatility of application is thought to be an expression of evolutionary development, instead of a mere spawning effect into different niches of the same ocean.
Yet, despite the many applications to which Mathematics has been rendered, and even though such rendering might well be interpreted an expression of growth, population density can not actually be used as a measuring tool for accuracy in establishing the presumption of actual development in terms of evolutionary advancement, as is often concluded when one looks at lower number values compared to higher number values such as from two to three germ layers. Population density plus specialized externalized adaptations acquired which may be labeled as racial configurations... for example, in a statement such as "different races of Mathematics," is not a factor to be dependent on in a criteria focused on determining what is meant by growth in evolutionary terms. In as much as Mathematics is situated in very many activities suggesting a level of exploitation having created a dominant role, does this alone provide for a substantiation that Mathematics is a higher form of "life" (conceptualization) and will continue to be so? Or has it reached a limitation in its ability to evolve beyond its present system of socio-economic-environmentalism? In other words, are we seeing a limit to the uses of Mathematics which requires humanity to persist in the present models of business, government, religion and other institutions? Has humanity chained itself to an evolutionary limitation because of its mathematics which is herein being viewed as antiquated?
There are multiple examples one might offer in analogy, if such an analogical model of comparison is at all a viable consideration. Let us take for example all the many life forms which do not indicate any step-wise development towards a "higher" life form, because such a transition appears to be locked into a cycle of imposed conservation. If we had all life forms expressing a characteristic evolutionary grade of "advancement" to some supposed "higher" life form, would basic biological processes cease to exist because they all "had to" evolve? Similarly, if all laborers went to school to be managers or all managers became business owners and there were too few people developing into a new cycle of laboring and instead chose to jump over such a stage of employment, would commerce thus be forced to create a robotic laborer force because all humans had evolved beyond even the management and ownership states of being? Like wise, what keeps humanity in a state where the use of "lower" forms of mathematics remains viable and human cognition does not take an evolutionary jump into a higher form of cognitive activity some might want to describe as a higher form of consciousness? Whereas the educational information being required of today's youth is more intensive than that of previous decades, is there a limitation and is this limitation being in part determined by the limitations of the type of Mathematical organism being permitted to survive like some invasive species which educational systems want ever child to be suffused with by way of accommodation and applied usage thereof?

Are we to be a species acting as a collective culture that survives in a singular type of environmental setting (in this case looking at mathematics as if it were a fishing village dependent on one or a few water-based commodities like clams, lobsters, whales, sponges, etc...), only to find itself to having become so dependent on such a resource; that its dwindling value of application beyond a select group of those who like the particular commodity in its raw or commercialized form; either forces further adaptation or becomes faced with the prospect of demanding the world revolve around it by keeping development in a stagnant state? I am of course pursuing the present course of thinking about the need for developing a new species of Mathematics generically described as "Accordian Calculus", because I viewed the present state of Mathematics as a primitive organism (like algae) that has been permitted to grow into islands of sediments like reefs that become islands upon which humans plant their flags and call home. It is a cycle of dependency that has developed in many ways like a symbiosis and accepted as being both normal and an expression of evolved life. Nonetheless, I view the state of Mathematics as a primivity which has created both illusion and deception which has lulled the mind of humans into a complacency that it is unable to see that such a dependency can act like an anchor, binding the further development of humanity to a given shoreline of conceptualization from which it is fearful of weighing anchor and traveling beyond the current beaches of Mathematics with all its charms of convenience and familiarity.
This is the state of Mathematics which I see being taught, whereby we have millions of students the world over learning to create pretty (and some very weird looking) mathematical formulas (most often as routinized exercises), and are able to perform set mathematical exercises that are then labeled as an expression of having a smarter brain and therefore a smarter populace (such as the long drilling requirements of education expected by some Asian and other academic institutions). Whereas some may value a student body with adept skills of mathematics being taught and required in order to compete in multiple sectors of a commerce-oriented society, what then if it is shown that such a mathematics training is the expectation for perpetuating an antiquated model of thinking in and of itself, as well as the expected standards of exercised thought in other subject areas of so-called higher levels of perception and interpretation?
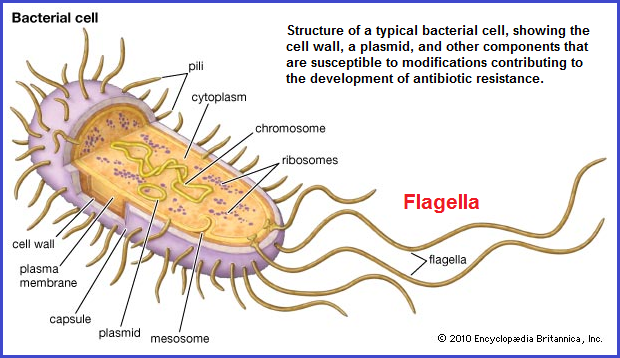
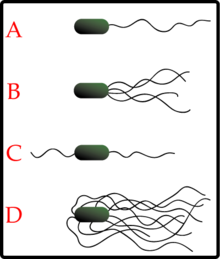
Like an early oceanic life form, the so-called dynamism of Mathematics is in its largest part, due to surrounding ocean currents and not some inherent self-mobility such as with flagella. (Writing a mathematics equation onto a piece of paper or board and then tossing it into a moving current does not make it self-mobile.) However, in using an analogy from biology to describe a primitive development of Mathematics should not lead one to reflexively consider it will follow the excursions of developmental biology towards a greater complexity. Mathematics as I see it comprises a state of existence comparable to a pre-Germ layer formula which is presently required as a precursor for the development of more complex life forms. Argue all you will against using biology as a descriptive analogy to Mathematics; when it is rather hypocritical on the one hand to view mathematics in an anthropocentric fashion by labeling it the "Queen" of all subjects, and yet disclaim the use of any other biological referent.
Very frequently, a comparison between Mathematics and Language becomes apparent as a necessity for understanding one or the other or both. In such a rationale, there is need to mention the absence of underlying mathematical applications to music theory developed into a musical composition by those who were born deaf, even though some individual may come to understand or appreciate music by way of rhythmic impulses garnered from vibrations. Likewise, it is of particular interest to invoice the absence of mathematicians who were born deaf, unless they become adept at substituting the need for language in developing "mathematical compositions" in a manner suitable for their particular model of comprehension which typically comprises an adherence to already established mathematical formula and queries. Like the beginnings of Mathematics which required the establishment of a particularized vernacular, jargon, idioms and associated symbology, taking mathematics development into a "higher" evolutionary stage of existence may well require the adoption of a new model of ideology commensurate with a language enabled to approximate the vistas of comprehension derived from an enlarged panoramic investment of conscious exploration into the subtleties of perception ingratiating the preliminary impressions accompanying an expansion in consciousness. No doubt others perceive this but have not as yet articulated it in a manner relative to their personal ability to use as a foot or hand hold in their own efforts to reach a higher plateau of realization which their own minds are prepared for and have either been awaiting the first glimpse of a new dawn or the light of a new day to break through the fog or clouds of a past they want to remove themselves from by mentally walking upright after dropping out of the currency of brush, bushes, brambles and trees that the greater whole of humanity insists upon calling reality, but is in fact a distortion, a disclarity, a discoloration thereof.
And though the idea in many contexts is to lead a reader towards some evolved or higher or climatic point of contemplation, it is of need to intersperse this ideological sojourn much preferred by some perspectives, with the actuality of one's intellectual internalizations with periodic reflections to historical or symbolically referential analogies concerning enumeration and how it can be used in different contexts. Hence, as part of the foregoing habit of interjecting examples of early counting that have been made into games, let me provide an image of an established card game called poker, though during individual moods of play amongst friends, the stated rules of the game may be altered according to the whims of one or more players who think such a change adds to the flavoring of the game in a given context, much like substituting one product for another or one type of accounting system for another, either to improve one's chances of winning, or stack-the-deck in order to give another or others the impression they can easily win and therefore should have no reservation of making a large enough bet (money, property, service, etc...) to satisfy the greed of those who have altered the rules to advantage themselves in the long run. Looking at how playing cards can be alternatively played in different settings gives us a look at the different types of enumerating schemes the human mind can indulge, and yet the use of cards limits or constrains human mental activity to perform within a given set of parameters due to the medium (types of card) being used. For example, when I was much younger playing cards with friends, we routinely permitted the dealer determine how many cards were to be dealt out and which cards (if any), were to be wild and how many points they were worth. We often chose the Queen of spades to be worth 40 points and called it "Queen 40". We might alternatively or simultaneously describe the one-eyed jacks as being wild, along with whatever numbered card the dealer wanted. On occasion we would play with two decks and on a rare occasion three decks of cards. On one occasion we encountered a friend who had never played cards with us before, becoming upset by our collectively agreed upon rule of "Dealer makes the rules". To our astonishment, he could not make the mental adjustment from one dealer's rules to the next, and left the game because in his mind, we weren't playing the game "the right way", that is... according to the rules he was accustomed to as directed by the rule on the small booklet which accompanied some card game packaging. None of us realized how single-focused he was, but ending up working as a lawn cutter for a golf course which expected a regimented routine of maintaining the golf course was something he was well "suited" for.

It is widely assumed that every card game has official rules specifying the only right way to play. This is like saying that there is only one correct form of a language and that all dialects are invalid. In fact, the vast majority of card games are folk games. Like dialects, they vary from region to region, sometimes from village to village, and they may change with time and be in a constant state of development, though it is true that some card games are inherently resistant to change—a notable example being cribbage, which has hardly changed in 400 years.
Games acquire official rules only when they become popular enough to be played in clubs and tournaments that attract players from widely different regions. It then becomes necessary to ensure that competitors from different "dialect" areas follow a set of rules codified in advance rather than having to negotiate each game as it is played. Where official rules exist, therefore, they are to be taken as the official rules of a particular governing body rather than those of the game itself. Bridge is one of the few games whose official rules, as promulgated by the World Bridge Federation, are universally followed. More commonly, official rules exist alongside local rules. Poker, for example, is equipped with agreed-upon rules in casinos and international tournaments but throughout the world continues to be played domestically in thousands of variations, some uniquely local and temporal, as in the play of dealer's choice.
Official rules are often credited to a fictitious authority called Hoyle. This name derives from the English whist tutor Edmond Hoyle, whose A Short Treatise on the Game of Whist (1742) proved successful enough to elicit sequels (some far from authoritative) on other popular games of his day. Success also led to his being plagiarized and his books' being pirated by his contemporaries and subsequently to the habit of attaching his name to any collection of rules of games, regardless of who wrote them or what their own authority was—a practice that persists in the United States, though not in Hoyle's native country, where his name is considered old-fashioned and irrelevant.
What most people mean by "official rules" is a clear description of how a particular game is played—the sequence of activities that define and distinguish one game from another. Such defining rules must be distinguished from procedural rules, which govern the corrections and penalties for mistakes and breaches of etiquette and constitute the bulk of any set of tournament rules, and from rules of strategy, designed to be helpful rather than mandatory. Given such distinctions, it is perhaps ironic that Hoyle himself never wrote a clear description of how any particular game was played. Taking for granted that everyone already knew the defining rules of a game, he had only an interest in outlining the strategy for playing it well and in compiling tables of odds for gambling—for onlookers as well as players.
"card game." Encyclop#230;dia Britannica. Article by David Parlett. Author of Oxford History of Board Games and A Dictionary of Card Games.
If we begin our search for furthering the steps beyond our socially (mathematically) constrained consciousness by re-examining the steps our personal lives as well as the collective life of humanity in its development of language and mathematics, a route such as the counting games used by children might be able to provide us with some measure of insight of which path to take in the present sojourn. However, before briefly embracing such a consideration, it is of need to point out some of the exercises children repetitiously engage themselves with (and into adulthood), based on playground equipment not all,but many children grow up with in current (at least) 1st and 2nd world countries. The point being that I would like the reader to recognize a substantial routinization of using polarizations, much in the manner which one might consider bipedal walking of the species has created conformational psychic patterning as an influence on ideas. Such examples as the up and down state of the teeter/totter, the up/down-to/fro of a swing, and the cyclical start-to-finish orientation of a Merry-go-round. Granted that not all kids are privy to such playground equipment, it is of interest to point out that such influences would seem to assist children in being able to develop a proficiency in a model of mathematics which similarly rely's on two-patterned repetitions, but proves not to be the case, at least not in cultural settings where children are psychically bombarded by various visual and auditory repetitions involving patterns-of-three.
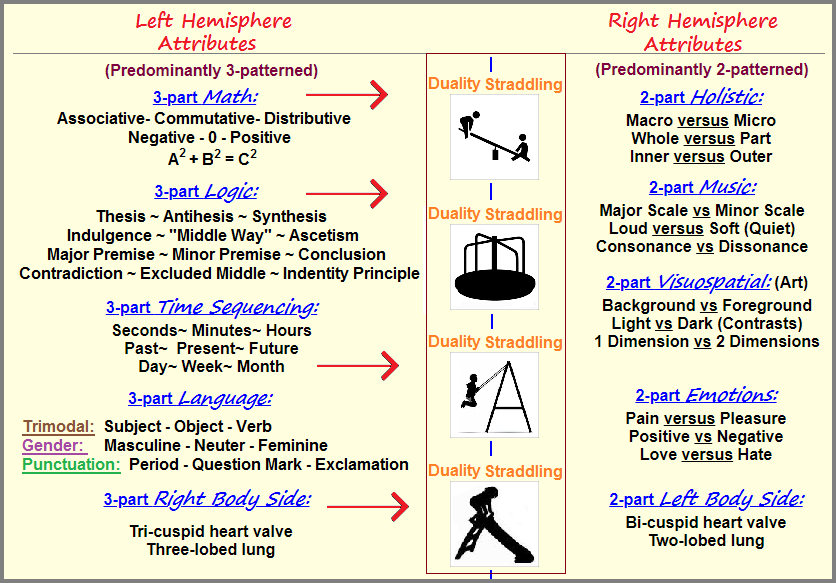
However, before sharing the aforementioned two-patterned functioning playground equipment forms, let me also make mention of Mathematics and Language once more, in correlation with brain hemisphere attributes, despite all the arguments disagreeing with the attributive pairings. Nonetheless the idea remains a useful addition to the present topic if for nothing more than denoting the fact that both Language and Mathematics have been focalized as characteristics of the left hemisphere, and the left hemisphere is a later-born contributing development of higher functioning abilities preceded by the right hemisphere and reptilian divisions, with the latter said to be nearer to the brain stem. In others words, by taking these three structures into account, we find the reptilian part of the brain developing first, then the right hemisphere followed by the right hemisphere. In other words, numerically sequentialized, we have a 1, 2, 3 stepping stone fashion, with the right hemisphere growing ahead of the left hemisphere according to tomography scans of infants. If we then look at the attributes assigned to the different regions, with the idea of self-survival interests as a singular orientation related to the number one, we can more easily assign the value of "2" to the right hemisphered and "3" to the left hemisphere. Interestingly, the right hemisphere attributes can be viewed as patterns-of-two and the left hemisphere attributes as referencing patterns-of-three. In still further words, there are states of transition between each of them, where patterns-of-two exist between the right and left hemispheres. Here is a chart providing a visual representation of the idea:
Children's simple chase-and-tag games involving the use of counting themes (like counting used to initiated a game of hide-n-seek which I played as a child under the name of "go-sheepy-go"), can take on greater complexity with the addition of rules and physical requirements for correct behavior, which frequently becomes designated by staying within lines such as when using a coloring book or playing the game of hopscotch; or later as adults by staying on designated hiking trails as well as obeying rules on paved roads whose lines earmark what should and should not be done.
(Hide-and-seek is an) old and popular children's game in which one player closes his or her eyes for a brief period (often counting to 100) while the other players hide. The seeker then opens his eyes and tries to find the hiders (those who are hiding); the first one found is the next seeker, and the last is the winner of the round. In one of many forms of the game, the hiders try to run back to "home base" while the seeker is away looking for them; if all of the hiders return safely, the seeker repeats as seeker in the next round.
The game is played differently in various regions; sometimes the seeker may be helped by those he finds. Alternatively, only one child hides and is sought by all the rest, as in sardines, where the hider is joined by seekers surreptitiously as they find him (the name of the game coming from the crowded condition of the hiding place). Hide-and-seek appears to be equivalent to the game apodidraskinda, described by the 2nd-century Greek writer Julius Pollux. In modern Greece hide-and-seek is called kryfto.
The game is played throughout the world. In Spain the game is called el escondite, in France jeu de cache-cache, in Israel machboim, in South Korea sumbaggoggil, and, in Romania de-av-ati ascunselea. Hide-and-seek is known throughout South and Central America under such names as tuja (Bolivia), escondidas (Ecuador and Chile), and cucumbé (Honduras and El Salvador).
There are many variants on the game. For instance, the Igbo children in Nigeria play oro, a combination of hide-and-seek and tag in which the seeker stands in the centre of a large circle that has been drawn in the sand and tells other players to hide. The seeker then steps out of the circle, finds, and then chases the other children, who must run into the circle to be safe. The child touched before reaching the circle must be the next seeker. ("hide-and-seek." Encyclopædia Britannica.)
(continued on next page)
Page Series origination: March 22, 2022, 6:57 AM
Initial Posting: 8th August 2022, 9:09 AM
Updated Posting: 2nd January 2023... 10:45 AM