~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
In some instances (other than mere favorite cultural numbers... though subject areas themselves are sometimes viewed as cultures with their own respective languages and social hierarchies), there is need to make note of the presence of two combined numbers (such as values from 10 through 99), or three combined numbers (such as values from 100 through 999), or even more than three (thousands... etc...). In several cases (such as the numbers 13 and 666), we need to label these reference in accord with the time period to which they arose (were perpetrated) and how they are being perpetuated. Some referenced numerical values are more ancient than others and that the origin(s) of such needs to be determined in order to differentiate standardized cognitive themes across cultures over time, and those which are cultural-specific for a given time period.
No less, the number combinations do not need to reflect an accustomed to natural number sequence one might expect such as when counting from a lower to a higher number. Then again, one might argue that the Fibonacci sequence is a Natural number sequence because this is how "Nature" uses it... which begs the question of whether humans can rely upon Nature to define all circumstances of a "Natural" number valuable to humanity in all circumstances, even if the word "Natural" is derived from the word "Nature".

Since the natural sequence of counting is to have odd and even numbers follow one another in a conventional sequence, the presence of what may appear to be an anomaly needs to be paid some recognition if for no other reason than a conscious acknowledgement which is referenced for others to make note of. However, in most instances the examples being given represent singular number uses (such as 1,2,3); though it is necessary to note that in multiple cases words or symbols are used instead of numbers. Unless practiced at doing so, a person might not routinely translate a number word (for example "few, many, some") into an actual representative quantity that is formerly visualized, even if such words as "few, many, some" are viewed as arbitrary designations to which different people assign a preferenced quantity. In other instances even straight-forward number words such one, two, three, etc., may not receive a conscious "translation" into a visualized number (quantity) value. Humans appear to all too often to take number words for granted, though if asked, they might readily provide an enumerated value.
In a different type of quantitative example, one might express three (word) items in a sentence (such as "persons- places- things"), but never label this as a "group" or "set", or "ensemble"-of-three. Or one might reference an X,Y,Z axis and not alternatively describe this as a set-of-three. In other instances it may be typical for someone to use number words (zero, one, two, three... etc.) instead of an actual number, because someone might prefer to include a familiar word without intending it to be referenced in any actual numerical sense. Indeed, it may be customary for some to routinely use symbols such as a . (period) and/or ? (question mark), but not intentionally reference this a recurring usage of (as a quantified) "two" quantity of sentence-ending punctuations, though there are three (., ?, !) [period, question mark, exclamation point] available for use in the English language. In addition to overlooking this quantity-of-three which may have been recognized as such very early in childhood, it may not be common to find that children are taught to also identify the quantity of using three fingers (technically: two fingers and one thumb) with which to hold a pen, pencil or even crayon and art brush. We humans very often take acts of quantification for granted which occur commonly in our lives, and therefore also overlook the frequency by which a particular number pattern is used more than others and those many number patterns used less frequently or not at all; as expressed cognitive behavioral characteristics. The presumed counting abilities of some animals (also insects? plants?) appears to be a non-conscious act one might label as an adopted behavior of adaptation alternatively described in some instances as an instinct.

One of the subjects I have been looking at is Mathematics, and yet, when I say that I want to use mathematics to analyze mathematics, don't expect the usage of elaborate equations other than to point out the simple patterns being used within an equation such as (for example) the dichotomies known as:
- plus/minus
- subtraction/addition
- multiplication/division
- positive/Negative
- rational/irrational
- etc...
The use of dichotomies in mathematics gives me the impression of a Westernized application of the old (Easternized) Yin/Yang idea applied to multiple ideas involving medicine, astronomy, physics, philosophy, etc., although such instances were applied in very ancient times. Yet, we see the usage of dichotomization in present day studial excursions into multiple interests that one may cite for example an application in computer language design based on the electrical circuitry of an on/off switching interval taking place at accelerated speeds. The application (or removal) of speed, pressure, temperature, sound, emotion, quantity, quality, height, distance, depth, etc., can significantly alter circumstances of activity as well as perception. A difference in the on/off switching phenomena can be viewed if we animate a switch to exhibit different speeds:
 A common 'person speed' of switching. |
 After drinking coffee or an energy drink. |
 A very slow computer switching speed. |
One might say that the language of computers and mathematics shared a kindred spirit in the sense of an underlying preference of using dichotomies, even though a Boolean type of mathematics is added to computer language scenarios so as to increase the dual nature to occupy a "three" language one can describe as the And- Or- Not profile sometimes described by using another dichotomy such as by applying true and false (statements).
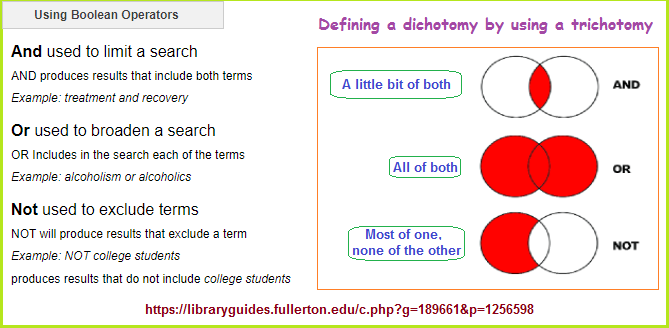

The recurrence as well as the absence of recurrence of particular patterns can help us to identify basic cognitive strategies underlying the processes used in mathematics. (However, the absence of a given pattern may well signal the absence of a strategy model.) It is similar to noting the strategy one uses to perform the activity of putting a picture puzzle together. Whether one starts by putting the edges together, compiling colors and shapes together, or some other preference such as collecting and putting together the corner or edge pieces first (as a type of pre-assembly behavior). In multiple instances you may find those who mentally/visually sort pieces as they assemble the puzzle, whereby the dichotomy of pre-assemble/assemble become combined as a type of "AND" Boolean logic option. Whereas some people use words more than numbers, we must have a means of exchanging ideas expressed in words, with numbers, if numbers do indeed help to achieve a greater truth for some occasions. Whereas it is pretty simple to change the word "two" to the value "2", an idea expressed in a sentence or paragraph may not make itself readily available for such a "translation" such as for example: "I ate a peanut butter and jelly sandwich". While one might alternatively describe the contents of the sentence in enumerated linguistic terms or devise their own method of interpretation such as by way of dissecting the object of discussion into constituent parts (such as itemizing the peanut butter/jelly and (one or) two slices of bread) to provide some countable numerical measurement; I will strive to stay away from such a method of analysis which might be viewed as arbitrary... though if calculated, arbitrariness might also reveal an underlying pattern of repetition.
the strategies used for putting a puzzle together can be seen as patterns in different cognitive tasks such as Sociology, Psychology, Politics, Economics, Military/Business operations, Medical treatment, Philosophy, board games, gambling, etc., including Mathematics. We might want to use the term "logistics" if such a word is more comfortable for the vocabulary of a given reader. Let us look at a general line-up of operations one or more people might alternatively use for putting a puzzle together. Next to these considerations will be placed alternative descriptions simply by adding differing terms:
- Dump out or remove pieces selectively or by handfuls. (Be assertive/aggressive or less so.)
- Place all pieces face up to show the picture or design. (In order to better survey the landscape/territory/environment for preferential interest.)
- Group according to perceived portraiture color, design or puzzle piece shape. (Assign a hierarchy of preference and accommodation or interest/disinterest ratio.)
- Attempt to assemble only similar pictorial colors or patterns. (Select by way of surface or superficial quality.)
- Attempt to assemble only similar shaped pieces which may be aided by external features. (Selectively chose by relationship values foremost, and secondary attributes secondarily or tertiarily.)
- Attempt to assemble by corner pieces. (selectively choosing assumed "cornerstone" features as a presumed advantage.
While the reader may use alternative descriptions by way of a given vocabulary suited to their preferential interest(s), the point to be made is that we are dealing with a basic cognitive functioning which can be alternatively described in simple numerical terms using words such as singularity, dichotomy and trichotomy, or the And- Or- Not terms seen in Boolean Logic. Multiple alternatives are possible.
In my attempt to show that Mathematics uses a preferential orientation towards a usage of patterns-of-two illustrated with formulas which might alternatively be described as dichotomies, parallels, pairs, dualities, etc..., I will venture into other subjects to provide examples of both similar and alternative patterns being repeated elsewhere, in order to validate the presence of recurring patterns which typically exhibit small number values (such as one, two, and three). (For example, one might alternatively point out the double helix structure in DNA, but not describe its triplet code and 4 amino acid bases, whereby we have an overall three-patterned 2-34 ensemble, not including the presence of a 3-to-1 ratio when we note that DNA and RNA share three of the same kinds of amino acids {adenine-cytosine-guanine} and one distinction noted respectively as thymine and uracil.) By claiming that Mathematics uses a dominant orientation towards a pattern-of-two but that other subjects apparently focus on another pattern such as three (or else-wise), the contrast will help to highlight the presence of a given pattern along with its absences. For example, If I say that patterns-of-three is a dominant theme, it is necessary to point out that in Astronomy, there is a dominant currency to speak of binary star groupings. In other words, if a pattern-of-three is important in Nature, why then doesn't the pattern exhibit itself in the observations of Astronomers, unless we speculate that the subject of Astronomy has a history and subtle academic requirement for being focused on the usage of a pattern-of-two such as binary systems. A subject with an ages-old beginning might well retain one or more preferences for a given quantitative orientation such as some people who claim a preference for the number seven, though they may not actually tell you why such a number was chosen even though later in life they have adopted supportive examples to qualify such an interest.
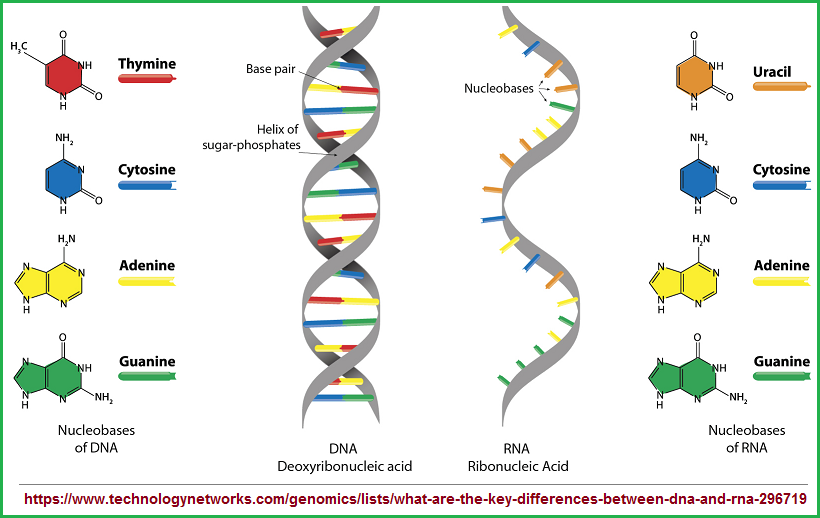
If we include the "single" (one/1) strand in the equation, we come up with a 1-2-3-4 count, along with the 3-to-1 ratio reference. In terms of numerical sequentiality, the single strand of RNA would thus represent an earlier biological model and RNA is in fact suggested as having arisen on the scene of developmental biology before the double strand of DNA. however, this is not to say that Nature cannot nor does not engage in different ("funny", "unusual") counting sequences which feature reversals, fractional digressions, skips (such as counting only by odd or even number values); or even introduce a type of enumeration that we humans (because of school-taught repetition and expectation), tend to imposed our own frequency of number usage on. In other words, due to the type of mathematics (and counting) we are brought up with, we are inclined to impose these values on all observations. If we find our mathematics or counting sequences "not working right", we might claim we do not have enough variables or provide some other excuse.
The stars in globular clusters are packed in much more tightly than in any other place in a galaxy. That leads to the creation of binary systems, including those with compact objects: white dwarfs, neutron stars, and black holes. Theoretical calculations show that exotic binaries, such as white dwarf-neutron star pairings, happen about 100 times more often than in the rest of the galaxy. Many of these systems are potential sources for LIGO and future gravitational wave observatories. (Star Clusters)
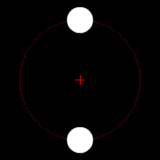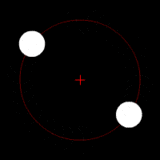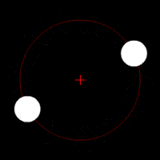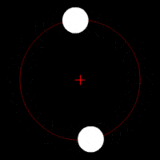 Two bodies of similar mass orbiting around a common center of mass, or barycenter. |
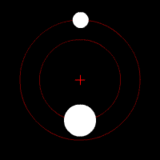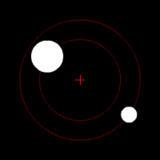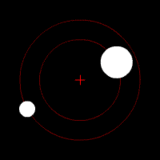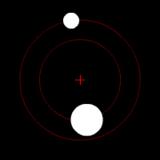
Two bodies with a difference in mass orbiting around a common barycenter, like the Charon-Pluto system. |
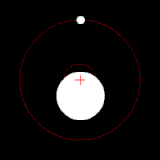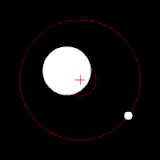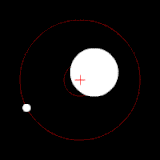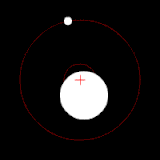 Two bodies with a major difference in mass orbiting around a common barycenter (similar to the Earth–Moon system). |
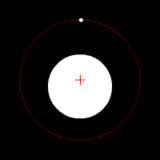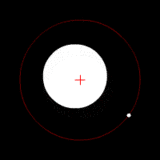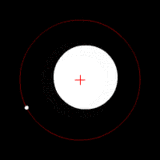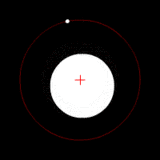 Two bodies with an extreme difference in mass orbiting around a common barycenter (similar to the Sun–Earth system). |
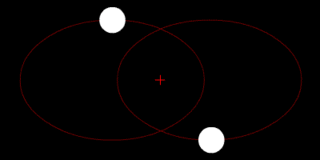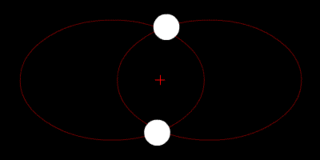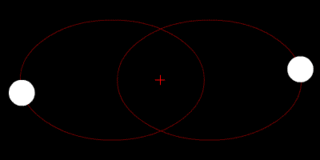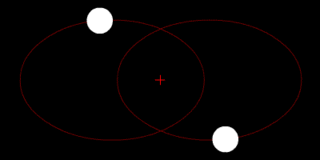 Two bodies with similar mass orbiting in an ellipse around a common barycenter. |
| Source: Wikipedia: Binary Star | ||||
While we can note the usage of a pattern-of-two (termed a binary) in star clustering phenomena, we can also describe the Earth as being the third planet from the Sun. Hence, a different... and major example of a non-two pattern must be noted, though both these enumerations are due to human interpretation. One can only wonder if some other species would use some other means of labeling and reference. And though we might well claim that both of these examples are "Natural" occurrences, the numerical labeling may not be as "Natural" as human might want to claim. Nonetheless, we have some human-related sense of referencing which other humans can understand.
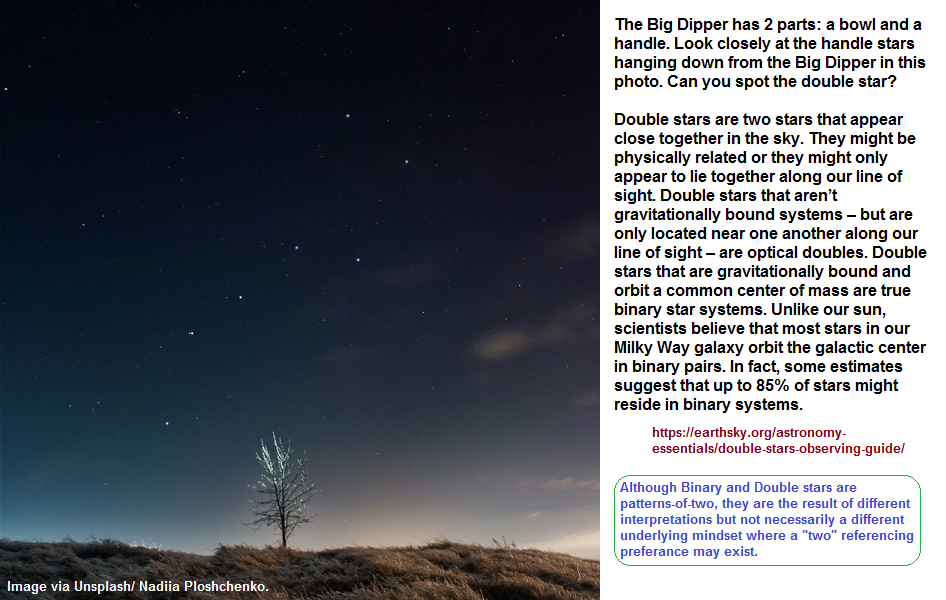
While the Big Dipper does have a double star cluster, it is the more prominent seven stars which have influenced interpretations applied elsewhere. Nonetheless, the idea of clustering and grouping might be used to claim a distinctive differentiation as a means to detract from the perspective that despite the labeling, both have an identifiable pattern-of-two. The idea of labeling quantities with different words or symbols which accompany different contexts may be used by some to equate the same relative quantity with a superior position as opposed to another. Take for example we emphasize the value of three in the reference to the Earth being the third planet and the value of two with the ages-old idea of Yin/Yang, and then from personalized perspectives suggest one is more important than the other. While we can claim that some enumerated references suggest greater importance based on a Nature versus human conceptualization comparison, let us not lose sight of the presence of a particular number value as a basic identifier. Just because we attach some superior position to a word does not mean it is superior, such as for example using the word "god" to represent either one or all, and yet overlook the presence of other singular items simply because we think the word "god" is to be set aside... up and above all other singular references.
Another example of the Binary is in the usage of zeroes and ones as a basic formula used in computer language aligned with the off/on characteristics of an electrical circuit. I make mention of these two pattern-of-two examples which some readers might be inclined to use as justification for the usage of patterns-of-two in Mathematics, instead of taking stock of the overall patterns being used in different subjects in order to make a more informed judgment. While the "two" may be claimed as natural and normal, let us also place it in the context of examining biological development (which involves the development of the brain in the sense of increased intelligence), so as to note that the presence of the "two" is frequently a part of a three-pattern sequence of development such as the one- two- three germ layer usage of primitive to more complex life forms. This review suggests that the "two" lays in a more primitive position as would be the case when thinking in terms of sequentiality. This being the case, then let us suspect the usage of "twos" in mathematics as a primitive cognitive orientation in need of further development, to the extent we need a new fundamental approach to the creation of a mathematics to viewed as superior, just as those who are attempting to build a quantum computer with a three-part language to replace the current two-part language.
This is not to say that patterns-of-two are not useful, since those who have been brought up with simple tools can well adapt to their usage and be quite adept for many practical applications, it simply states a different model of mathematical thinking may be possible to develop, similar to those who developed a more efficient three-field system of farming as opposed to the old two-field system involving Crop Rotation. Another example of a one- two- three developmental scenario can be seen in the history of Accounting:
...Although the Double-Entry Accounting method of bookkeeping was much more advanced and efficient than Single-Entry Accounting, still there were several flaws in this too... ...Thus, Triple-Entry Accounting is a step ahead of the traditional Double-Entry Accounting; one that will relieve the bookkeepers and companies from tedious troubleshooting and help remove the mistrust, frauds or manipulations faced by them... (Triple entry accounting system: A revolution with blockchain by Kapil Rana, Mar 27, 2020)
In some examples, I have found both a two and three pattern which some observers might count as a "five", thus leading to a situation in which the presence of higher (beyond "1") numbers should be scrutinized in order to identify whether using a composite valuation is an accurate interpretation. An example of the 2/3 can be seen in DNA with its double helix and triple code; and yet we can also see a "4" in the presence of amino acids (adenine-cytosine-guanine---thymine), or describe this as a three-to-one ratio when we include the presence of RNA and its differentiated "Uracil", thus presenting us with a phrase "three the same, one is different" portrait. Hence, the 2/3/4 (or three-to-one) is an ensemble of three as a pattern in its own right. Hence, we can find the 2/3 situation in mathematics as well, along with other (more than two and three) patterns, but that there appears to be a dominant presence and usage of patterns-of-two that suggests an unrecognized cognitive primivity leaving room for the development of a Mathematics with a dominant three-pattern, and not simply the usage of a given singular mathematical form such as trigonometry to suggest Mathematics incorporates multiple patterns and is therefore at its developmental best which no one can supersede in creating a "better" model.
In as much as modern Astronomers speak of binary star clusters, let us not forget that ancient peoples were transfixed on other enumerated patterns such as the seven stars of the Pleiades, the seven stars of the Big dipper, and the usage of the seasons as a platform to view the position of the stars so as to create a compounded view such as the creation of the Swastika from the Big Dipper seen during the two Solstices and two Equinoxes. The identification of the "seven" stars was subsequently adopted by some religious perspectives as representing some important god/heaven theme or message. The point being, different perspectives can adopt a particular orientation culled from the same information. The more dynamic the observation... whether the context or content, may well have a dramatic occurrence on what is observed. We might refer to this as a traffic accident scenario. In other words, a bystander to a traffic accident might well have a different interpretation than someone involved in the accident. And those involved in the same accident may well have a different perspective relative to their trauma, shock, and injury level. An ancient primitive person experiencing a loud thunder clap accompanying a flash of lightning, may well interpret the event quite differently from a supposed modern day educated person.
The Mathematics being used today, though it has been described as having an "Unreasonable Effectiveness in the Natural Sciences", needs to be analyzed from a variety of perspectives, one of which is the application of mathematics to itself; despite any claim that the effective of Mathematics may falter in any attempt of "self-analysis" due to presumed constraints involving objectivity. It goes without saying that those who are practiced with crude instruments are nonetheless capable of applying such instruments with adept facility and dexterity to the point of giving an impressive display of talent. However, despite the entertainment value and practicality of application, the usage of number to analyze perceived basic patterns is of value, though pattern may more often use words than numbers. For example, instead of using a plus and minus symbol to indicate a feature used in mathematics, one might encounter the words positive and negative. Nonetheless, both symbols and words indicate not only two qualities, but they are a paired featurette common to the usage of mathematics. In several cases there is need for a researcher, an analyzer of mathematics, to translate words into number values.
Recurringly used basic values in mathematics are often relegated and thereby regulated as operational parameters providing a means to distinguish limits and otherwise assumed limitlessness. Take for example the case of the word "infinity" which may philosophically be juxtaposed with a notion such as "zero", if not words such as nothingness, emptiness, void or some other attribute conveying the notion of being opposite-from-infinity, but nonetheless paired and thus represent a pattern-of-two. Understanding the value of enumeration to cognitive processing requires the adoption of analogies from biology, if not other subjects such as physics and chemistry which strive to simplify the activities of Natural occurrences so as to minimize the reproduction of observations from a biased or prejudicial orientation which might be otherwise interpreted as a personalize perception which could easily be alternatively described and thus provide a different interpretation which could create a situation of questionable legitimacy. In multiple situations we use mathematics as a tool that will provide us with a basic, unwavering representation of truth. Such truths very often show up in the form of numbers representing values with one, two, or three numbers associated together such as the colloquial expression of Pi being 3.14, despite those who extend the value to several more places such as 3.141592653589793238. (What Is Pi, and How Did It Originate? by Steven Bogart on May 17, 1999).
Cognitively speaking, the human mind does not have a number or quantity value beyond the single number "9". Values beyond this symbol require the usage of two single numbers such as 1-0 to produce the value of 10. Interestingly, if we ask a person what their favorite number is, they may well express a single number. It is not common to ask or be asked to describe one's favorite numbers, (in the plural), though the common interpretation of such a question may evoke more than one single number or numbers representing two numbers or three numbers such as 13 for the first and 333 for the next. Asking someone for their favorite "numbers" as opposed to favorite "number" is so uncommon as to present a person with a situation which they may not be readily able to provide an answer other than some incredulous reply as a type of knee-jerk response. Nonetheless, the point to be made is that a person's number typically becomes represented with ones, tens or hundreds. Values beyond this may be atypical for some occasions and even be the result of someone wanting to appear to be different than others whom they are listening in on as they supply their number interest(s).
In the case of particle physics, while there are several fractions for the state of charges, (such as 1/3, 2/3), one can view these as represent single or double numbers, though again we see the presence of low values being expressed. It is uncommon to hear someone say (for example), that their favorite number is 1111111111111111111111111111111111111, or some other large number. Even though we find examples of larger-than-a-three number value in chemistry such as the Wikipedia: Octet Rule (Rule of Eight).
the overall value is represented with a single number just as we find in genetics with a triple code. In other words, Nature does not express itself with larger number values. Much like developmental biology which appears to use a one-two-three maturational development sequence as noted by the usage of three Germ layers or three states of matter (gas-liquid-solid) or number place notation in which humans use a comma to mark off the ones-tens-hundreds from the thousands (etc...), as if to progress by way of using triplets or three-patterned ensembles; there is no reason to expect human cognition to do otherwise. Indeed, for it to do otherwise might well present us with a circumstance where the human mind via its physiological processes has reached a point of exceeding the dictates of its masters (genetics, chemistry, physics) as they govern the underlying developmental processes of biology.
But the reader needs a list of multiple patterns-of-two in order to provide some measure... and thus merit... to the present discussion concerning the need for analyzing mathematics to point out the presence of a primivity which humanity needs to develop beyond and create an existence that is not dictated by the application of dichotomies as if humanity is stuck in the developmental stage of a life form exhibiting only two... instead of three germ layers. (See for example: The Embryo Project Encyclopedia). Animals (except for sponges) are said to grow from three germ layers (termed triploblastic animals); with more primitive life forms arising from two germ layers (term Diploblastic) such as the Cnidarians. Though controversial, it is sometimes viewed that the sponges (which are animals), do not have either three or two germ layers, and may thus constitute an example of a primitive animal with one germ layer. I would term this a state of being "Monoploblastic", if I may be permitted to coin a word to reference this state-of-being.
Conversely, I propose that human cognition frequents the usage of its own type of "1-2-3" developmental sequencing by an exhibited representation of these values, though the three may be expressed with a single word such as three, third, trinity, treble, triune, triad, triaxial, etc... The absence of such a usage may well signal a cognitive primitivity, even though a person whose usage of "two" or a two-pattern is either preferred or required due to environmental/social circumstances, may use a "three" as a garment without an active cognitive usage other than playing it some measure of lip service. In other words, what they say is not what they actually think or use as a cognitive tool.
In describing the need for a different type of mathematical reasoning, not only do we explore the prevailing types of maths in an effort to catalog recurring patterns such as the aforementioned dichotomies, but also how such an orientation may have come about by way of environmental influences over time as physiology developed with recurring patterns itself that can be enumerated. No less, we need to describe other-than-human instances of basic (or complex) maths usage such as presumed counting abilities and those activities one might describe as geometry, trigonometry and even calculus, though the human mind might be inclined to describe such acts as rudimentary exemplified by the construction of a spider's web, bird nest, system of tunnels, etc..., used by different creatures and frequently noted in non-mathematical terms such as being the result of instinct.
Take for example an ant colony. While humans generally describe three types of ants labeled Queens, Males, and workers, one must wonder if the ants themselves use "3" as a self characterization, or is this just a convenient imposition created by human perception? In any respect, the following excerpt suggests that ants have at least a rudimentary means of counting, as described by an experiment using three different alternative modes of travel:
Harald Wolf of the University of Ulm and his assistant Matthias Whittlinger proposed that ants have "pedometer-like" cells in their brains that count the steps they take.
Wolf and Whittlinger trained a bunch of ants to walk across a patch of desert to some food. When the ants began eating, the scientists trapped them and divided them into three groups.
- They left the first group alone.
- With the second group, they used superglue to attach pre-cut pig bristles to each of their six legs, essentially putting them on stilts.
- The third group had their legs cut off just below the "knees," making each of their six legs shorter.
After the meal and the makeover, the ants were released and all of them headed home to the nest while the scientists watched to see what would happen.
The "Pedometer Effect"
- The regular ants walked right to the nest and went inside.
- The ants on stilts walked right past the nest, stopped and looked around for their home.
- The ants on stumps fell short of the nest, stopped and seemed to be searching for their home.
It turns out that all the ants had walked the same number of steps, but because their gaits had been changed (the stilty ants, like Monty Python creatures, walked with giant steps; the stumpy ants walked in baby steps) they went exactly the distances you'd predict if their brains counted the number of steps out to the food and then reversed direction and counted the same number of steps back. In other words, all the ants counted the same number of steps back!
Does that mean ants have something like pedometers that do something like counting?
Says professor James Gould of Princeton, commenting on the experiment: "These animals are fooled exactly the way you'd expect if they were counting steps."
Gould says it's pretty clear ants don't have maps in their heads and don't recognize markers along the route. This experiment strongly suggests that ants do have internal pedometers that allow them to "count" their way home.
Ants that Count by Robert Krulich, November 25, 2009 9:01 AM ET
The above example illustrates how a research technique involving a certain pattern involving a quantity, may well influence the results. In this case, there were three groups of ants associated with a give ability, resulting in a three-into-one alternative answer... out of which was established a three-part variation concluded with the idea that the ants may have an ability to sequentially count. Whereas one can argue that the use of two or more-than-three groups of ants would have provided the same results or provided a mixed review, this could suggest that the "three" value may be routinely used not necessarily in terms of "fixing the game" so-to-speak, but as being part of a fixed game where human cognitive activity is unknowingly being subjected to a form of manipulation constructed by an incrementally deteriorating environment.
If one takes a survey of different experiments that have taken place, one might find that there is a recurring numerical theme such as three subjects being used, a three-day, three-week, three-year study by three researchers or three groups of researchers using three different methods.
The same can be said for those who use the tools of mathematics which is fashioned from the mold of dichotomization which at times spills over into the realm of trichotomy. Whereas some may call mathematical thinking normal and natural... albeit due to training one's mind how to think within the parameters of a proscribed emphasis of dichotomization which some may want to describe as a superior model of consciousness superior to "common sense" because their ego has a need for such a recognition; the fact remains that recurring forms of quantity can act as channels or rain gutters for further perceptions.
One must inevitably ask whether it is of value to keep using a two-part tool such as mathematics on three-part constructs, or must we eventually have to accept the fact that a three-part tool is most appropriate? A simply analogy may be to describe mathematics as a dichotomous stop/go traffic light but that reality requires a three-part stop-caution-go tool as complexity (quantity of vehicles) increases as a means to impose some semblance of order on what might otherwise be chaos. If we then describe, for examples, trigonometry as a three-part tool, are we actually representing an underlying orientation of dichotomization in a three-part way, such as applying the And- Or- Not idea to the binary form of electrical switching used in present day computers?
Page Series origination: March 22, 2022, 6:57 AM
Initial Posting: 8th August 2022, 9:09 AM
Updated Posting: 2nd January 2023... 10:44 AM
