~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
If an animal (such as an ape) has a main diet of one staple such as that we define it as a herbivore but may at times supplement its diet with insects (insectivore) and small animals (carnivore), the singular (primary) dietary orientation may or may not be used by some observers to suggest the cognitive orientation is similarly singular in orientation; most due to the fact that human definitions of "singularity' or even "primary" may be insufficient in creating a viable enumerative model of description which can be transferred to other life forms and their eating habits. For example, one might be inclined to count all forms of a plant diet resulting in a larger-than-one description, thereby leading them astray from the initial attempt at using a system of enumeration as a tool with which to both analyze and organize perceptions. However, if they can keep from indulging in a "many" script and focus on smaller enumerations like the descriptive tallys used by some researchers in different fields, they may will enable themselves to approximate the realization of a recurring pattern that can be useful applied across multiple subjects. It's not that one may encounter large number examples, but that the larger numbers may not themselves have a large range of occurrence. Small number patterns have a wide range of application and are often elaborated into providing appearances of larger numbers or larger complexities (as an expressed reflection of a researcher's large ego); by way of the words, phrases... that is, labels employed in describing multiple small number occurrences they may become overwhelmed with and attempt to contract into a manageable... serviceable quantity they can adequately memorize and facilitate into a comprehensive illustration that others may be able to make use of from their individualized perspectives.
While we have a Mathematics with a dominant orientation using an underlying two-patterned formula, and have mathematicians readily observing the presence of these patterns by sometimes referring to them as dichotomies, this realization is not being further analyzed in terms of cognitive development as an extension of biological development which, for example, references this same pattern in multiple exhibitions such as the bilateral body plan, the mouth/anus (in/out) duality, and various other instances of pairing that one cannot help but see in activities such as the previously noted double-slit experiment which is not conceptually easy for some people, thus giving the impression they are either "slow" in mind or obversely, "fast" in mind in the sense it is difficult for them to visualize what may be described as a simple... if not primitive orientation. Let us revisit the experiment from this idea of conceptual difficulty. Notice that a Boolean logic parameter of "OR" is employed when describing the A and B slits as options, except that the overall logic is like a rigged musical chairs game involving two active (and one passive, side-lined) player, and one chair, though one might rearrange this situation to confer with their underlying logic not exposed to the same critique which a person uses in critiquing other views, and thus admits to a discriminatory (if not hypocritical) bias.
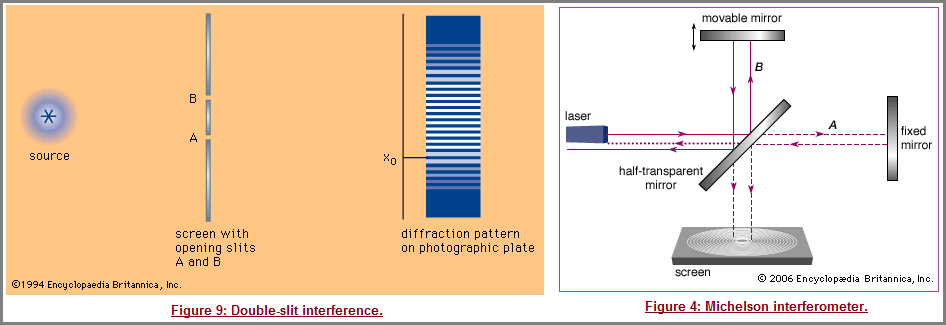
The interference pattern that results when a radiation front hits two slits in an opaque screen is often cited to explain the conceptual difficulty of the wave–particle duality. Consider an opaque screen with two openings A and B, called double slit, and a photographic plate or a projection screen, as shown in Figure 9. A parallel wave with a wavelength ƛ passing through the double slit will produce the intensity pattern on the plate or screen as shown at the right of the figure. The intensity is greatest at the center. It falls to zero at all locations x0, where the distances to the openings A and B differ by odd-number multiples of a half wavelength, as, for instance, ƛ/2, 3ƛ/2, and 5ƛ/2. The condition for such destructive interference is the same as for Michelson's interferometer illustrated in Figure 4. Whereas a half-transparent mirror in Figure 4 divides the amplitude of each wave train in half, the division in Figure 9 through openings A and B is spatial. The latter is called division of wave front. Constructive interference or intensity maxima are observed on the screen at all positions whose distances from A and B differ by zero or an integer multiple of ƛ. This is the wave interpretation of the observed double-slit interference pattern.
The description of photons is necessarily different because a particle can obviously only pass through opening A or alternatively through opening B. Yet, no interference pattern is observed when either A or B is closed. Both A and B must be open simultaneously. It was thought for a time that one photon passing through A might interfere with another photon passing through B. That possibility was ruled out after the British physicist Geoffrey Taylor demonstrated in 1909 that the same interference pattern can be recorded on a photographic plate even when the light intensity is so feeble that only one photon is present in the apparatus at any one time.
(electromagnetic radiation." Encyclopædia Britannica.) Excerpt from article written by Hellmut Fritzsche, Louis Block Professor of Physics, University of Chicago. Coauthor and editor of Advances in Disordered Semiconductors (2 vol.).)
I can almost draw to a close this particle-wavy duality example of cognitive activity related Mathematics but first need to round it off at the edges by making a definition-like reference from the Britannica because it provides a rather fortuitous introduction of the idea concerning another two-patterned idea called complementarity.
(The wave-particle duality references a) possession by physical entities (such as light and electrons) of both wavelike and particle-like characteristics. On the basis of experimental evidence, the German physicist Albert Einstein first showed (1905) that light, which had been considered a form of electromagnetic waves, must also be thought of as particle-like, or localized in packets of discrete energy. The French physicist Louis de Broglie proposed (1924) that electrons and other discrete bits of matter, which until then had been conceived only as material particles, also have wave properties such as wavelength and frequency. Later (1927) the wave nature of electrons was experimentally established. An understanding of the complementary relation between the wave aspects and the particle aspects of the same phenomenon was announced in 1928 (see complementarity principle)... "wave-particle duality." Encyclopædia Britannica.
Complementarity principle: In physics, tenet that a complete knowledge of phenomena on atomic dimensions requires a description of both wave and particle properties. The principle was announced in 1928 by the Danish physicist Niels Bohr. Depending on the experimental arrangement, the behaviour of such phenomena as light and electrons is sometimes wavelike and sometimes particle-like; i.e., such things have a wave-particle duality (q.v.). It is impossible to observe both the wave and particle aspects simultaneously. Together, however, they present a fuller description than either of the two taken alone.
In effect, the complementarity principle implies that phenomena on the atomic and subatomic scale are not strictly like large-scale particles or waves (e.g., billiard balls and water waves). Such particle and wave characteristics in the same large-scale phenomenon are incompatible rather than complementary. Knowledge of a small-scale phenomenon, however, is essentially incomplete until both aspects are known. ("complementarity principle." Encyclopædia Britannica.)
While the idea of complementarity in mathematics is known, philosophically speaking, I came across one on-line article which explicitly referenced the view using this word in the manner to which I was thinking (Complementarity in Mathematics, by W Kuyk). [I wanted to read it, but like so many items I am interested in, they are all behind some sort of pay-wall or "by the book" platform, and the costs for some of the items I would like to read are in the range of several hundred dollars each. So much for the internet providing a source of knowledge to everyone everywhere at the tips of their fingers.] Other philosophically oriented mathematical ideas within the same context use the word "complimentary". In many references advancing an idea about the conceptual framework of Mathematics, we find some semblance of an attempted historical overview. Some are better than others and no doubt many are much better than my own. But I am trying to provide multiple references about the different avenues of both influence and application which the underlying two-patterned basic Mathematics orientation has. In so doing, I must make comparison with other influences and influencers involving enumeration, particularly those which emphasize the presence of enumeration, though an author may not necessarily be cognizant of the act of doing so. Let me adventure into another area with these thoughts in mind.
Ideas, theories, and structured systems of thought also are incorporated into religious symbolism. Abstract ideas—such as wholeness, unity, and the absolute—and the power of the spirit are concretely expressed in religious terms. The idea of unity plays an important part in expressing the oneness of the divinity. Mathematical principles expressed in number symbolisms are used to organize the world of the gods, spirits, and demons, to describe the inner structure of human beings, and to systematize mythology and theology. The concepts of duality or polarity find expression as the body and soul of man, the divine pair, the syzygy (paired emanations) in gnosticism, the dualism of God and the Devil, of good and evil, and, finally, as the two natures of Christ. The number three, or triplicity, is represented in divine triads, the Trinity, and the body-soul-spirit structure of a human being, as is the number four, or quaternary, in the four cardinal points, the picture of the cosmic whole, and the divine quaternary. Time and eternity may be expressed in abstract symbolical terms as well as concretely in picture form. ("religious symbolism and iconography." Encyclopædia Britannica.) Excerpt of article written by Kurt Moritz Artur Goldammer, Professor of Comparative History of Religions and of the History of Religious Art, Philipps University of Marburg, Germany. Author of Kultsymbolik des Protestantismus.
If we say that religion predates Mathematics, then we need to look at religion as a precursor to Mathematics, in which we should be able to identify the beginnings of Mathematical ideas, language and symbolism. And yet, what predates religion? Did religion predate numbers or was it the other way around? And thus speaking of which came first, let us ask what was the first type of consciousness? And do that or those which predate consciousness create impressions that are later used as scraps (or "wholes") of material from which to construct conscious portraits... most of which are not chronicled in any surviving medium except for perhaps bits and pieces of socially influenced interests that we call crude stones and other artefacts... similar to the interests which are learned by most people in and out of mandated schools of thought and activity, many of which are due to commercial exploits?
If all, most, or some of Mathematics origins originated in mental and then later written lists of accumulation and methods of divestiture such as in bartering for other goods, then we have another instance of duality playing a major part in the construction of Mathematics that became exercised as a necessity and then recreated variations appeared as games of chance involving gain and/or loss, just as when one engages in a business. All games are played with an underlying duality involving a win or loss, with a draw as a seldom used third attribute, because human ego strives to create an interpretation of a win or a loss. And if one says this is the nature of Mathematics which draws it cue from a similar pattern found in Nature such as life/death, smart/dumb, strong/weak, male/female, etc., then such arguments overlook the very point I am making, and those who pursue a three-based quantum computer can be said to be exercising a similar mutagenic exercise as one encounters in a three-chromosome individual such as with Down syndrome. Yet, if chromosome count is of concern due to the incremental deteriorations of the larger planetary system and 'smaller' earthly environment, one might want to take another look at the grain crop staples of humanity since our attention appears to be directed to such sources by the Crop Circle makers; even though humans are more interested in looking at the "pretty pictures" and using a two-based mathematics to envision some sort of communication is taking place conveyed in geometric designs no one has yet configured into some numerical sensibility. Perhaps the many designs are an attempt to get humanity to take a closer look at the structure of crops from which to glean a greater knowledge from all the chaff caused by not interpreting the simple system of creating crop circle designs by "knocking over" the plants as a means of conveying we need to look elsewhere for a primary food source such as creating a dominantly viable three-chromosome plant structure.
If adding a third to a two, such as adding another chromosome to humans causes undesirable effects, is this the case because we have the wrong double-based chromosome for such an effect, in that adding a three to a two appears to serve us well when adding a triple-format Boolean logic to the binary code of computers. We have also added a three-based system of accounting for the two-based night/day sequence, with the advent of the second- minute- hour model of calculus. Similarly, we use a three-medal (gold- silver- bronze) with respect to a two-based win/lose situation in the multiple games of chance (enumeration) played in the Olympics. No less, one might speak of the Heaven/Hell dichotomy and yet the existence of a trinitarian idea in some Christian perspectives, or the Trimurti in Hinduism. It's as if the human mind is stuck attempting to achieve a "full three" practice and can only make a preliminary step in that direction. The situation is further compounded by a social insistence of using a two-based mathematics to force the human mind to conform to its structure... or else, we are taught... our thinking is wrong if it doesn't agree with our mathematics, even though we often adjust mathematics to fit the reality in which we live. On the one hand it imposes, and on the other hand we see it as an imposter... an imposter that inveigles its way into a position of dominance at a later date and thus creates the same structure of imposition once again.
So many are obsessed with making Mathematics the dominant tool of intellectual activity, thinking processes which do not use mathematics to confirm their view, is said to be incorrect, though someone later on may create a new mathematics which agrees with the processes. It's like a religion that practices a system of confession to find out what the flock is thinking, in order to maintain control over them by contouring a system of belief conducive with the rationale the people want to collectively agree with and in turn provide the religion with funding so as to perpetuate a given perspective. Like religion, Mathematics can be an effective system of practiced superstition that acts as an invasive parasite into all human activities with different methods and manners. And yet, what would be the state of human affairs if it didn't abide by the present state of religion-like Mathematics with its commandments called axioms and its wares applied to superstitious orientations?
How is it possible to develop a new calculus of thought if the present model had its influential origins in an environment of religious irrationalities which no longer have the influence, power and control over populations as they once did? Does the development of a new Mathematics require a different kind of perceived oppressive irrationality and/or a different type of commerce? And if we were to strip Mathematics of its dichotomous past (and present), will it be of a structure the common person can not appreciably understand or use for their dichotomous fixations of reality? Just like many people not understanding the simplistic binary code of computers, or that mathematics is primarily based on a dichotomous structure, the same will no doubt be for a triune based computer language and Mathematics. What I am describing is not a middle point between two extremes, but three separate points interconnected as separate entities and not as out-growths in a three-germ layers sense of construction. But if a "three" can only be constructed by way of a "one" then "two," is a "three" little more than an embellishment of a 1 + 2, and a "two" an embellished 1, regardless if we use words or symbols?
If mathematics is little more than a mental extension of biological processes, then unless we either wait for Nature to alter humanity or engage in some intentionality of restructuring, no "greater" type of mathematics is possible. However, if one prefers to think that Mathematics owes its origins to religion, or philosophy or war or commerce, etc., then there may be no greater mathematics to arise unless such exercises are themselves developed into greater practices... an not merely convolutions of simplistic orientations being compounded with multiple components which give the impression of complexity because it satisfies the intellectualized egos of those involved. Then again, because humanity has not yet unraveled all the patterns in biology, chemistry, physics, linguistics, etc., the present state of Mathematics may grow in the direction which best serves to representatively elucidate those patterns into a visual schematic... before it can "grow beyond itself". That is, grow beyond its Janus-faced structure and compartmentalizations.
Let us nonetheless proceed on the assumption mathematics may have had some earlier influences at its inception, but it has come to mature on its own. And while it may have a larger dichotomous base, there are mathematical practices which are meant to divest itself of this predominant orientation and bias. Let us proceed with the notion that Mathematics is its own person much like the three-patterned colloquialism noted as "Free, White, and 21". That in still other words, it has come of age, having met the challenge of a rite-of-passage, and run the gauntlet attesting to its worthiness of being a full-fledged member of the human intellectual community; instead of as an infant remaining in a babbling stage sucking on a baby bottle or a child still soiling its pants and clinging to a stuffed animal.
While some may claim that Mathematics resembles a type of rhyming system (of song and dance), this perspective needs to be confronted by a simple examination which easily reveals the current practice of mathematics does not have any words which rhyme until we reach the suffix repetition of "teen" in the seven numbers recognized as 13,14,15,16,17,18,19. The next "rhymes", (by way of repetition) are seen in the next double number instances of twenty (20, 21, 22...), thirty (30, 31, 32...), etc. Then we get into the rhymes of triple number composites, and so forth. We first have one-word number rhyme repetitions and then two-word number, then three-word, etc.. (A two-word number rhyme example begins in the hundreds category by repeating the hundred and then the successive 20, 30, etc... The Three-word number rhyme example begins in the thousands category, and so forth.) In this sense, there is rhyme in numbers, though some readers may attempt to apply a larger "poetic license" and claim they see additional rhyme configurations. Nonetheless, the point about rhyme occurring in Mathematics has been made, and I feel there is no need to belabor the point for the present context.
One can use a system of axioms to construct a coherent sentence within the parameters of the axioms, just like one can play a coherent board game within the parameters of rules accompanying a game from a manufacturer. Interestingly, if a society wanted to encourage mathematics thinking by introducing a public to its language, all manufacturers should be required to provide their rules under the heading of "Axioms", with the word "rules" in parenthesis below it. In some instances we already see the application of simple multiplication in the form of describing how many pieces are included, such as in the case for putting together a piece of furniture with different quantities and sizes of screws, and other parts. It is of some interest to note that I have never encountered a mom or day in any household referring to their cooking in a mathematical sense of measuring or deciding how much of something is or is not "supposed" to be used. Cooking and baking require mathematical based measurements, though some cooks and bakers use a "pinch" of this and that. However, I have heard some parents telling their kids not too think too (so) much because it wasn't good for them. Which suggests that those who do think come to survey their life and the possibility of removing themselves from it to be a remote chance, and it is better... under such circumstances, not to think too closely about a situation which may make them turn to alcohol or drugs to numb their consciousness away from a conscious realization of their circumstances due to the "fixed" systems running rampant in human society in this era. Many people come to realize that they are smart enough to see the undesirability of their circumstances but not smart enough to know how to leave or improve the conditions. Having opportunities is one thing, knowing about them and how to navigate the swampland of bureaucracies to get (to) them is another.
Rules of a game just like the different axioms of mathematics can be contoured to fit the intellectual personalities of those invested in taking part in the exercises, for fun or profit. However, in taking an example from the lumber industry, the usage of numbers by manufacturers may say one thing, and the actual size can be quite another. For example, a 2 inch by 4 inch by 8 foot board is a "rounded-up" measurement similar to the "Big" (as in a "Big" burger) in use by advertisers wanting to conceal that a smaller size is actually being offered. Similar to this is the 9/10ths designation on fuel pumps. It was put into use when gas cost pennies per gallon and governments instigated a tax requirement. The habit remains as a deceptive practice when the cost is displayed 9/10ths of a penny lower than it actually is, such as in the case of $4.50 9/10. In other words, the cost of this gas is almost equal to $4.51. It is a penny-grabbing tactic that is used, but since the 9/10ths is displayed in many cases, the actual cost need not be consciously registered. The point is, numbers can be used to deceive as well as elucidate. Yet, laws that are used if they are axioms are not based on any standard rule of equality or an ability of the public to make changes to the axioms when they are found to be faulty. Legislators, business owners and religions abide by their own self-constructed axioms to serve the purpose of financing activities which the public has no say over; and thus we have three types of axiomatic systems of social discourse that frequently provide us with a false logic, and the "real" axioms of "real" mathematics has no rule governing how numbers are to be used.
As many people realize is the case with how polls can be skewed according to what, how, when, why, by whom a poll is written and provided, so to is the case within the chambers of accounting where "creative" (number-fudging) activities can take place to falsify reality. Whereas one might say that Mathematics is not perfect or that it is but humans are imperfect, both cases apply to the view I am stipulating for the need of a new model of Mathematics. If luggage is being used (such as in a court room) to describe circumstances as adding up or not adding up, then a mathematics equation needs to be brought forth, except that this too reveals a deficiency of current mathematics... or at least its usage. Indeed, let me submit that it makes little difference (except in degree), whether Mathematics is faulty or those who use it. If it is such an exact science as some might claim by asserting its supposed royal status of being Queen, they why are there so many math mistakes and research into finding a purer model? This is because it is neither exact nor are its practitioners. Why is it sometimes the case such as when a discovery is made in Mathematics it might be called an Epiphanous event, only later to find it to be but a stepping stone to yet another "Revelation", much in the manner of high priests seeking some greater (closer) presence with their assumed god?
While one might indulge different philosophical inquiries, it is only of value to do so if it at least provides some direction we might survey in an attempt to discover a new model of Mathematics. Whereas I might say a "three"-based pattern based on a biological modeling framework which can be used to contrast itself with a "two-pattern," there is no reason why such a mathematics "has to" exhibit such an identifiable pattern. Though we might claim that the series of numbers from 1 to ten are a ladder, scaffolding or segmentation, not all life forms exhibit metamerism like an Earthworm. Understandably we might say the Germ layers is a type of fixed enumeration just as the quantity of organelles in plant and animal cells, we do not obligingly refer to them as metamerism, just as we do not refer to the lineup of amino acids or the arrangement of atoms in a chemical compound as a type of segmentation. Neither do we commonly describe keys arranged on a phone or keyboard as expressions of metamerism, though the repetitions of designs employed suggest we are dealing with an unacknowledged uniformity of cognitive expression put into general usage.
The use of any word, in this case "metamerism" alternatively labeled and thought of as serially organized segmentation can be problematic when its use in one context with several similar examples, leads some to specialize words for specific references since researchers themselves are segmentally arranged in a particular discipline of study; whereby alternative applications of the same word(s)— particularly to other subjects— may not be permitted even in their own discipline. Let us take the information from the following Britannic excerpt for example:
Segmentation also called metamerism, or metameric segmentation
In zoology, the condition of being constructed of a linear series of repeating parts, each being a metamere (body segment, or somite) and each being formed in sequence in the embryo, from anterior to posterior. All members of three large animal phyla are metameric: Annelida, Arthropoda, and Chordata. The first two exhibit conspicuous segmentation in the adult. Among the chordates, the repetitive metameric pattern is evident in muscles, vertebrae, and ribs of the adult (e.g., fishes), but even when less obvious (e.g., mammals), the development of each individual is based firmly on formation of segments, the embryological somites. Segments of the tapeworm (proglottids) are formed so differently from the segments of the other three groups that most zoologists do not admit tapeworms to be metamerically segmented animals. Since the metamerism of Annelida and Arthropoda and that of Chordata probably arose independently, metamerism does not itself imply relationships between the groups; however, the particular metamerism within each group clearly demonstrates the derivative relationship of its members.
Among acanthocephalans, rotifers, and some other "aschelminth" groups, external ring-like formations, called annulations, occur in the covering tissues, sometimes so marked as to suggest segmentations; these formations prove to be only superficial, however, and are not indicative of true segmentation. ("segmentation." Encyclopæ\dia Britannica.)
Notice the previous sentence ends with "true segmentation". It is "true" based on arbitrariness conforming to multiple examples of a condition to which no other label is applied. "True" meaning repetition under a given set of circumstances by those sharing a similarity of thought processing and vernacular. Yet, such a view need not stop us from using the word "segmentation' (metamerism) in any situation where some seriality is present, even if the "presence" is an occurrence taking place intermittently or over vast ages of time. Then again, how many repetitions need to occur (regardless of shape, sound, color, distance etc...), before we label it segmentation? At least two but never one? Is this how we start a list of axioms which can be conferred as a "truth" if others use it as well? No less, does segmentation also imply grouping or in mathematical terms a "set"? For example, we may say 1,2,3 is a set but we might not readily describe 1,22,33 a set as easily as we might 1,22,333. Because it is common to see three items in a row as a series or set, regardless of what the items may be, this is not the case for all things in all contexts, perhaps because it is common for us to see a set such as 1,2,3... or apples, oranges, bananas, etc., as variations of the typical way many people make both numerical and non-numerical sets. Whether listed right to left or left to right, a series of elements might alternatively be described as a group or set. In other words, we permit ourselves to be flexible, but flexibility wanes when we encounter specialists striving to project their ego and reputation on a specific type of observation or that being observed. Many of us have not intensive ego investment in lots of different kinds of situations. We permit ourselves enough flexibility to own up to mistakes and not be unduly injured by that which may be more amenable to a larger scope of examples than is being used. Most of us do not take on the role of pretending to be a finish carpenter, when we know that rough-in carpentry is well enough for basic framing.
Unfortunately, if we use a "rough-in" framing sort of thinking to be applied to axioms, the final structure (equation) may be lopsided or even fall apart. But if axioms are equivalent to the attitude by which finish carpenters use, then what are the rules-of-thumb to be used by rough-in carpenters who imply they are neither novices nor journeyman? What practitioner's journey are they on? More importantly, did their rules-of-thumb lead to the construction of axioms which we require a specialized perspective not allowing for flexibility?
(continued on next page)
Date of Origination: 19th March 2022... 5:23 AM
Initial Posting: 8th August 2022... 9:10 AM
Updated Posting: 2nd January 2023... 10:50 AM