~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
If we view the frequency that certain number patterns occur in different subjects both individually and collectively, as well as in different combinations, the frequencies (as well as lack thereof suggested by the word "infrequency" and the notion of intermittent frequency), a researcher might think in terms of starts, stops, and jerking movements... all of which can have different durations. Nonetheless, it presents us with a model of information that traditional numerologists have tried to supply us with, but owning to the widespread disinterest in an activity that is most often off-handedly dismissed as being irrelevant, a larger study of a larger sampling from a larger subject base has not been undertaken. Commonly, there are those who frequently react to a "collection of threes" (which involves more than just patterns-of-three though it may be the originating dominant theme of a given task); as a rather quixotic pursuit of information consistent with a hobby of collecting some odd occurrence of a (typically) manufactured good/item, though there are those who collect only items to be found that have been manufactured by nature such as diamonds, shells, flat stones, triangular stones, fossils, butterflies, plants, leaves, etc...
When speaking of collecting, let us broaden our inclusion of labels: The term "binge" is often used as a prefix attached to words such as eating (binge eating) which might alternatively be called bulimia. A two-word phrase such as "obsessive-compulsive" might well be applied to numerous activities such as those pursuing some degree, reward, or occupation which requires an extensive (but frequently erudite or specialized) knowledge and skill(s). For those who transgress such a behavior the additional word of "disorder" may come to be attached, revealing a three-patterned phrase of "obsessive-compulsive disorder", whereas with respect to the single word "binge", the attribution of interpreting it to be problematic comes from its association with the second word, and its contextual application in social circumstances which may have labeled it as a negative activity. For example, the idea of "binge eating" has a negative connotation whereas the two-word phrase "binge reading" or binge watching (such as a particular television show or youtube presentations) does not typically receive the level of condemnation or derision that "binge eating" has accumulated. Within the present context of writing an essay about one perspective on the Philosophy of Mathematics, several collections of different information are required, and may thus also be termed a "binge" necessity, or even obsessive-compulsion, but not in attendance with the word "disorder", which is a word usually reserved for an activity that keeps one from performing other activities such as bathing, eating, sleeping, working, or otherwise engage in other tasks required for health and hygiene. An extensive collection of examples to be used to represent one's conjecture is a viable asset, though others may interpret such an activity to be too distracting for their own personal interests which may involve lesser cycles of binging one or another activities such as called a routine exercising regime, vitamin/mineral/protein consumption regime, cooking/washing tasks, etc...
For some, the collecting of number patterns found in different subjects defined as expressions of cognitive activity, seems to be a frivolous pursuit like someone engaged in the writing of poetry. some marginalized musical genre, or some other defined artistic practice that appears to be wholly impractical and will lead them to starvation as well as possibly being recognized not simply as an odd person nor as an eccentric individual, but an odd eccentric. And if one is born with such a demeanor, they can either come to excel in a recognized pursuit involving fame and fortune, or allow them to blaze a trail that others may impulsively react to as being foolhardy and the efforts of what used to be commonly called a ne'er-do-well (never do well). Whereas such an activity most often is only taken up by someone who has already established themselves in a "proper" business, religious, militaristic, political, or academic career, some of us are born to pursue a path not taken, be it on land, sea, air or outer-space. For me, it has been the pursuit of a path which picks up the cognitive trails of others in different subjects and activities. Only by making such a pattern of patterns over a long period of time from different subject areas and activities is it possible to better recognize the recurrence of patterns which will at times overlap.
Like so many different biological species having been collected for hundreds of years by different people from their respective genres of interest (philosophers, alchemists, astronomers, mathematicians, physicians, children, housewives, gardeners, etc...), such efforts came to be collated and assembled into a framework called a binomial system, mainly because a pattern-of-two formula of conceptualization was a dominant orientation of those who proposed themselves as an authority figure. By using a defined system of collation, other researchers were enabled to add to the list in both form and function from which has been derived an enormous amount of information regarding the placement of different life forms into the presently used three Domain system of classification. However, despite the multiple recurring patterns of enumeration of different ideas to be found in different subjects, no one has thought to collate them to the point of suggesting we have a genre of information that may be useful in not only understanding the development of human thinking processes, but also whether such processes are stagnant and deteriorating and what may be causing such occurrences.
Although cryptographers analyze a set of patterns in a singular subject such as transmissions within a military context, the thought of enlarging the context to include all subjects as the playing field or "theater" (a word adopted by the military to give the impression of sophistication), is typically negated as being a worthless adventure. Despite those who come to direct their interest to the singular context of words in order to identify which letters are used more often than others, the same idea is not applied to the presence of enumerations being exhibited in different ways in all subjects. Whereas one may speak of comparative anatomy, comparative music, comparative art, comparative cooking, and multiple other comparisons of singular subjects, the idea of collating numerical references in many or all subjects is a hands-off task because it does not present the possibility of someone establishing a financially fruitful career or social recognition having any value. Even though such was the case for all present day "honorable" subjects when they were first developed, this point about their early beginnings is somehow relegated to a position of disinterest except for those having an interest in the historical beginnings of a given craft, whether it be surgery, crop growing, knapping arrow and spearheads, fishing lure/net design, boat designs, weapon designs, scientific dating methods, etc.
For me, as an example of a graph to present the idea of developing a graph which highlights periodicities of number-pattern occurrences, a chart highlighting the frequency of occurrences concerning individual letters (in a given language such as English) can be used. One need only think in terms of substituting the usage of letters with enumerated patterns, and instead of limiting oneself to a single context such as words, one enlarges the context to include multiple, or all subjects, though the study of a single subject area may be all-consuming for a given individual whose interest is proportionately directed to one subject.
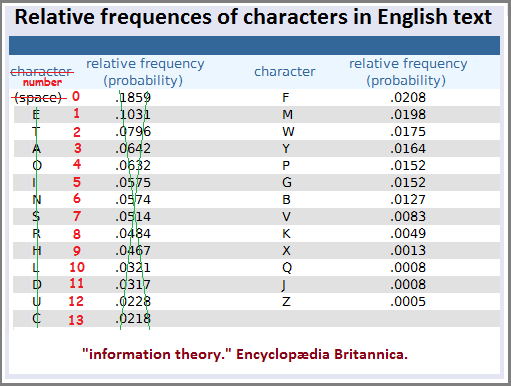
The above graph displays 26 letters (and space) from a singular context (the English language), though the sampling of words is not described. Another much easier descriptive is to make a graph displaying the relative frequency of how often a person uses a capital letter instead of a lower case one. Typically, a person used more lower case letters. If we substitute the 26 letters of the English alphabet with numbers, we might come to find that some of the numbers between 0 (indicated by the space) and 26 occur very infrequently, and that number patterns such as twos and threes occur very frequently as if being a form of vowel. As indicated by the (relative) chart above, vowels occur more often than consonants, with me viewing vowels as a-e-i-o-u... and sometimes y. If we use a vowel/consonant analogy, we find that the frequent occurrence of some number patterns can be called vowels due to their repeated occurrences, and some numbers as different consonants. This analogy suggests that the human brain may use a numerically-based system of consonants and vowels. However, we need to discover if a two and or three and other number patterns reflect a cognitive form of vowel, consonant or suprasegmental, unless context of application determines which of these forms are being used by the human brain. For example, let us say that the usage of dichotomies is a cognitive expression of a vowel in one era in one context, and then changes to a consonant in another era and contextual application. In other words, several centuries ago the usage of dichotomies was a vowel when applied to the subject matter of interest, but in a later century the usage of dichotomies was a cognitive expression of a consonant, with respect to a given subject-context. This is to say whether or not we can assign a dichotomy of vowels and consonants or a trichotomy of vowels-consonants-suprasegmentals to given number patterns.
Now let us take the same graph and count the frequencies that the numbers zero through nine occur in this example. The point being that there is a frequency, despite the "relative" proposition being made. Similarly, the usage of dichotomies appears to be used quite prominently in mathematics. Is this due to the human species having been taught this way a physiology not only designed by the character of the Earth's night/day, hot/cold, etc., environment, but reinforced by a bipedal gait, just like insects that may "think" in a predominant pattern-of-three orientation due to a prominent triad gait as well as a tripartitioned Head-Thorax-Abdomen body profile?


It is frequently found that developmental phases or developed attributes identified in Nature often become adapted for use by humans in their efforts to mechanistically, ideologically, or emotionally recreate such exercises such as in the case of adopting the gait of insects to robotic creatures in an effort to increase versatility in an otherwise crude and cumbersome collection of electrical, chemical, fluidic, and mechanistic contraptions. (The word "contraption" is not to be inferred as a depreciation of such trials and efforts to overcome obstacles with sincerity and dedication.)
The point is, we humans come to apply similar patterns of thought processing no matter the task. For example, many an insect has three pairs of legs, and thus we humans create insect-like robots with the same quantity of attributes. Perhaps because the movement of insects appears to be robotic at times. Simple life forms routinely exhibit simple movements to whatever terrain (land/water/air) they are adapted to. Similarly, complex life forms like humans create movements in accord with adaptive exercises commensurate with the range of environments they are subjected to, though such equations do not frequently take into consideration the incremental deterioration of the Sun, Earth, and Moon, which is a type of three-body problem of a different order. In any respect, if we take a look at one perspective of attention being paid to the prosed types of gait which might be applied to a six-legged robotic-insect, a 3- 4- 5 pattern emerges as if one is engaged in an alternative form of Pythagorean formula. In addition, these three need to be contrasted with the idea of a "free" model of locomotion as if to incorporate the ability of a robotic insect to have the means of negotiating any and all terrains regardless of their structure.

Like other examples used in different pages, I have labeled the quantity of gait types in the above example as an illustration of a "3-to-1" ratios instead of as a quantitative "4", because I think the distinction bears merit for fruitful examination in multiple research areas. Whereas the value "4" is used as a quantity following "3", we apply a "three-to-one" characterization when we count, and sometime in mathematical set notation. For example, we will write the sequence of numbers 123456789, and then add a comma after a group of 3 so as to separate distinctions of clustering which may give the impression of stuttering or babbling. Nonetheless, regardless of the attributive analogies one might care to assign, we use the measuring tool of including a comma to provide us with the sequence of 123,456,789. In other words, the sequence is grouped to present us with millions, thousands, hundreds. However, Nature apparently does not routinely use large number expressions of itself, at least not from a human perspective. For example, we have a three-to-one ratio in DNA and RNA when we cite that each of these has three amino acids the same (Adenosine- Cytosine- Guanine), and one that is (respectfully) different: Thymine (DNA), Uracil (RNA). Whereas humans routinely use three-to-one ratios, it is not certain that Nature actually "counts" in this way. Nonetheless, humans have adopted this behavior even if most people are not aware they use such a pattern.
Yet, just like sequential counting in that there may be no quantity beyond a thousands place (interpreted as a four-quantity), we can find examples which may include but not exceed a ten thousands place, whereby some interpret this as a five, but could readily be interpreted as a 4 to 1 or 3 by 2. For example, while some people say we have five fingers, another person may count the digits as four fingers and one thumb. Still another person may single out one or more fingers as have some particular distinction (pinky, ring finger, middle finger), whereby the described count takes on a different proportion. The point is, while we humans may be counting in one fashion, Nature may be "thinking" of quantity or functionality in a different fashion. In any respect, the aforementioned repetitive usage of a dichotomous orientation being used by Mathematicians may be a false configuration which acts as an obstacle to further development. We know how to look, but we don't know how to see. Our seeming obsession of using dualities as an underlying standard of mathematics appears to be a Westernized recitation of a differently styled yin/yang compilation over-which we embellish with patterns-of-three to provide us with the scenario that we add, subtract, multiply or divide one number in conjunction with another number in order to get a presumed third. I say "presumed" because humans rationalistically orient themselves towards adopting an attitude of an accomplished or achieved progression, when in actuality it may be little more than an adaptation to an overlooked incremental deterioration requiring a specific type of survival mechanism.
When one sees set figure sequences such as (1...), (1, 2...) (1, 2, 3...) and think this is a reflection of superior mathematics and not some repetitive cognitive illustration found in other subjects which use their own vernaculars to express the same pattern; how are we truly going to be able to discern a progressive development in mathematical thinking if we are simply using the same underlying patterns expressed with different symbols regulated as part of a larger survival mechanism that has been forced into usage by the presence of an incrementally deteriorating environment which most people would readily dismiss by using one or another rationalization as a defense mechanism?
This is not to say that mathematics doesn't have great utility, much like a stick used by a chimpanzee to flesh out a tidy morsel of an insect from some crevice, but the long term facility of such an adaptive behavior benefiting an individual in their respective life, ineffectually provides them with an ability to notice that the assumed progress defined by tool usage also embraces a foolhardy interpretation about the prospects of longevity for the entire species. In the world of chimpanzees, the usage of a stick can be useful... just like the usage of mathematics for humans. In this sense, mathematics is little more than a type of stick with which humans can probe, poke at and doodle a myriad of geometric forms with and call it science, art, poetry, music or even futility.
No less, let us view Nature itself (that which humans recognize in the context of our reality) as a primitive life form or life form originator which uses primitive patterns, whereby human deductions of basic patterns routinely portray the exhibition of small numbers (for example, we have a triplet DNA code and not a larger number code), which may thus reflect a stagnant developmental sequence that some readers might dismiss as due to the length of time required for Evolution to make changes. Yet, it is not certain if Evolution can make changes to its own Nature... that is, provide life forms with a different model of Evolution with which to evolve, or use some other mechanism other than that which we at present call "Evolution". Indeed, why do we see so many recurring small number patterns in basic Natural phenomena and yet attempt to dismiss this notion by claiming there are larger number patterns (beyond 1s, 2s, 3s, 4s, 5s...) such as the 8 (octet) pattern in chemistry, the 8 pattern in (octomerous) life forms, and the 7 or 8 quantity of Hox genes in free-living members of Platyhelmiths (Acoelomorphs have four or five Hox genes: pg. 292, Integrated principles of Zoology, ISBN 978-8-07-304050-9) yet fail to recognize that such an "8" pattern apparently occurs more often in primitive instances and is not widespread in multiple other subjects? And to this we might add the presence of a primitive "4" occurrence in quadripedalism with a lowered number bipedal gait used as a criteria for judging evolutionary advancement, at least in primates.
For example, why isn't there 8 families to atomic particles or people routinely being born with eight fingers, eight toes, eight eyes, eight heads, hearts, etc.? Why no eight-coding system for DNA and RNA? Why no 8-forms of DNA or a standardized 8-speed bicycle or 8-position selection on appliances and automatic transmissions, or eight children being born as a standard birthing quantity of all life forms or 8 cores as a standard in all computers? Why does Nature stop at using a recurrence of small number patterns unless for some reason it actually doesn't, and it is human perception/consciousness which is imposing the recurrent usage of small number patterns? Why does mathematics, not only in the presence of an infinity of numbers and a suite of small numbers to choose from (zero through nine), set a standardized dominant focus on using dichotomies, much in the same manner as the usage of a binary system for an electric circuit based computer language? Are mathematicians simply regurgitating some ancestral obsession of using patterns-of-two (like some Western born Yin/Yang formula), and will rationalize some presumed value to describe why such is the case, without taking the time to statistically arrive at a value which makes such a usage an improbability, or that such a probability is indicating we are dealing with an influence that is being overlooked? In other words, is the system of mathematics rigged to configure a mathematical rationale to offer some plausible reason for the persistent usage of an underlying dichotomization of views implanted in the construction of mathematics equations, typically resorting to some biological, atomic or mechanistic model to offer up a supposed proofing exposition?
We can recognize a recurrence of different patterns being use to express ideas in all subjects. All of them have some level in which basic patterns of a given subject matter are being indexed and in some cases such as comparative anatomy and embryology, we come to discern similarities of patterns exhibiting the same quantity. This is not to say that researchers are making the correct deductions, but that... nonetheless, some pattern is offered as being exemplary of a given process, function or design. At least how humans are perceiving such occasions. All told, we are dealing with information which can be filed under a heading of information theory that, not surprisingly, encompasses a usage of number relationships:
(Information theory is a) a mathematical representation of the conditions and parameters affecting the transmission and processing of information. Most closely associated with the work of the American electrical engineer Claude Shannon in the mid-20th century; information theory is chiefly of interest to communication engineers, though some of the concepts have been adopted and used in such fields as psychology and linguistics. Information theory overlaps heavily with communication theory, but it is more oriented toward the fundamental limitations on the processing and communication of information and less oriented toward the detailed operation of particular devices.
The formal study of information theory did not begin until 1924, when Harry Nyquist, a researcher at Bell Laboratories, published a paper entitled "Certain Factors Affecting Telegraph Speed." Nyquist realized that communication channels had maximum data transmission rates, and he derived a formula for calculating these rates in finite bandwidth noiseless channels. Another pioneer was Nyquist's colleague R.V.L. Hartley, whose paper "Transmission of Information" (1928) established the first mathematical foundations for information theory.
Clearly, the recurrence of number patterns in different subjects is information that we do not yet understand what is being conveyed to us. While the information is being transmitted just as electrical impulses of the early telegraph, suggesting that the patterns being revealed are like a type of Morse code or Braille, we have also come upon a circumstance reflecting the causal nature of certain patterns being more frequently repeated than others. Does such a situation reflect a primivity of thinking or an accurate depiction of a phenomena indicating we are subjected to a primitive formula of Nature in the present context of Earth, and that other forms of Nature exist with more complex formulations of processes, functions and structures?
While humans have unraveled the code of genetics and atomic particles (to some extent), the patterns being presented to us by recurrences in different subjects is not understood because such a discipline of study is in the position where all subjects begin such as for example paleontology. Whereas there may have initially been one or two who collected a few bones and used them as door-stops (so to speak), later on there were those who collected more bones and other items (which were later labeled as fossils), and still others who eventually saw the collections as representative of a pattern of life and geologic stratification. For example:
Paleontological research dates back to the early 1800s. In 1815 the English geologist William Smith demonstrated the value of using fossils for the study of strata. About the same time, the French zoologist Georges Cuvier initiated comparative studies of the structure of living animals with fossil remains. ("paleontology." Encycloædia Britannica.)
All present day disciplines had their formative beginnings with fits and fashions, starts and stumbles, as well as detractors. Whereas Charles Darwin (for example) made a collection of life forms while on his five year voyage: (The HMS Beagle was a) British naval vessel aboard which Charles Darwin served as naturalist on a voyage to South America and around the world (1831–36). The specimens and observations accumulated on this voyage gave Darwin the essential materials for his theory of evolution by natural selection. ("Beagle." Encyclopædia Britannica.)
If Darwin had not made the trip or had not made a collection with which to refer to, it is suspect whether he would have developed his "On the Origin of Species by Means of Natural Selection" (later called a theory of Evolution), even though the publication of the idea took two decades after his initial three-volume beginning and after he gained the distinction of being a Justice of the Peace. ("Darwin, Charles." Encyclopædia Britannica.) The point is others were not only thinking along the same lines, but were gathering dispersed amounts of examples which would later prove to help enlarge the underlying premise of Darwin's ideas. All the collections were necessary even if he did not yet have a conceptual framework for inclusion in his own ideas. Needless to say, the rather disparate looking information began to fit together into a puzzle from which a picture of life could be ascertained, and is extensively applied today.
The recurrence of enumerated patterns and those patterns not yet enumerated are presenting us with a sketch we can tentatively describe as representing a blueprint or map or etching of human cognitive activity. If you prefer, let us call it a paint-by-numbers dot-to-dot illustration that we have not collected all the numbers for in their respective placements. If low numbers being exhibited in ideas of fundamental occurrences represent that Nature itself is a primitive life form (so to speak), let us also identify what sort of species this life form is and whether it is able to evolve to a more modern formulation. If Mathematic's usage of a top-heavy dichotomous orientation is to be viewed as a fundamental/basic scaffolding, then is this due to an imposition created by the human psyche, the indication of an inherent disposition due to a primitive design (like an expressed development using two instead of three germ layers), or a relative "cry for help" because mathematics is being forcibly subjected to an imprisonment which forces it to curtail its desire for expressive freedom?
Continued on next page.
Date of Origination: 19th March 2022... 5:23 AM
Initial Posting: 24th March 2022... 3:24 AM
Updated Posting: 2nd January 2023... 10:59 AM