~ The Study of Threes ~
http://threesology.org
Visitors as of August 8th, 2022
| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |
| Page 6 | Page 7 | Page 8 | Page 9 | Page 10 |
| Page 11 | Page 12 | Page 13 | Page 14 | Page 15 |
| Page 16 | Page 17 | Page 18 | Page 19 | Page 20 |
Let me start this page off similar to the way I started the preceding page... with a reference to pre-math concepts in order to draw attention to the use of patterns-of-two that I have referenced as a "Westernized model of the Easternized Yin/Yang ordering system". The current system of Mathematics is often portrayed from the perspective that Mathematic's is described as a "common ground" of mental activity that can be understood by all sentient beings throughout the Universe; or a type of Sign Language (though there are many kinds: Sign languages) or alternatively viewed as a Lingua Franca:
lingua franca, (Italian: "Frankish language") language used as a means of communication between populations speaking vernaculars that are not mutually intelligible. The term was first used during the Middle Ages to describe a French- and Italian-based jargon, or pidgin, that was developed by Crusaders and traders in the eastern Mediterranean and characterized by the invariant forms of its nouns, verbs, and adjectives. These changes have been interpreted as simplifications of the Romance languages.
Because they bring together very diverse groups of people, many empires and major trade entrepôts have had lingua francas. If pidgins have sometimes been defined, less informatively, as lingua francas, it is because they evolved from varieties that had served as trade languages. Aramaic played this role in Southwest Asia from as early as the 7th century BC to approximately AD 650. Classical Latin was the dominant lingua franca of European scholars until the 18th century, while a less prestigious variety of Latin served as that of the Hanseatic League (13th–15th centuries), especially in its bookkeeping.
During the era of European exploration in the 15th–18th centuries, Portuguese served as a diplomatic and trade language in coastal Africa and in Asian coastal areas from the Indian Ocean to Japan. In Southeast Asia, meanwhile, Malay was already serving as an important lingua franca; it had been adopted by Arab and Chinese traders in the region well before the Europeans arrived. Later both the Dutch and the British used Malay for communication with the peoples resident in the region.
Modern lingua francas may or may not be officially designated as such: the United Nations employs six official languages (Arabic, Chinese, English, French, Russian, and Spanish); international air traffic control uses English as a common language; and some multilingual Asian and African countries have unofficial lingua francas that facilitate interethnic or interregional communication. Such languages may be erstwhile pidgins, as with Lingala in the Democratic Republic of the Congo, the Nigerian and Cameroon pidgins, or Hiri Motu and Tok Pisin in Papua New Guinea; they may also be non-pidginized varieties such as Swahili in East Africa or Hausa in West Africa. (Salikoko Sangol Mufwene)
Present day languages such as Italian and English had writers (and no doubt unrecorded speakers) who helped to solidify their usage, just as Mathematics is thought to be a solidified language that all sentient beings in the Universe can understand. With respect to Italian, the "three literary crowns" are Dante Alighieri, Petrarch, and Giovanni Boccaccio. Geoffrey Chaucer "in legitimizing the literary use of Middle English when the dominant literary languages in England were still Anglo-Norman French and Latin". Whereas we have linguists who dissect languages to uncover basic patterns, this is not the case with those whose research into Mathematics may be limited to focusing on the origination of ideas related to quantity from which the numerical (or number word) seriation of 1- 2- 3... developed, as well as describing when, who, and what a given type of mathematics was used for and may have evolved from some rudimentary beginnings. The fact that Mathematics is replete with dualities does not get that much attention, nor viewed in terms of a human cognitive process similarly exhibited in all other subjects and their respective vocabularies and applications.
While many of us are aware of the "1- 2- Many" reference to the development of enumeration by primitive peoples, and though this phrase may be inaccurate in some cases, it nonetheless serves as a useful generalization regarding early numbering systems. In Mathematics, a cognitive parallel may be the use of one number that is added, subtracted, multiplied or divided by another number, to get a third. Hence, a pattern-of-three can be seen, even while Mathematics appears to be predominantly focused on the presence of patterns-of-two, or a linguistically-based counting system that does not exceed the value of "2". With respect to languages, there is an established view of a "tripartite number" used as a marker:
Introduced by Dimmendaal (2000), the term “tripartite” has been widely used to describe the number marking systems of several Nilo-Saharan languages. According to the original definition, tripartite refers to the three different number marking patterns in which nouns in the respective languages can occur: singulative, plural and replacive. On the typological variation in tripartite number systems of Nilo-Saharan languages (Jan Junglas, HU Berlin)
And though we have a "dualism marker" when referencing examples for the Yin/Yang philosophy, the same is not being undertaken for a study of Mathematics. Many of the tools we use in linguistics or when making personally-organized inventories of different subjects, is not typically used when an analysis of Mathematics is undertaken. Far too many researchers are using Mathematics to define Mathematics and wouldn't think to apply colloquial suppositions to it in the same manner one might look at board games, sports, restaurant menus, etc... For some reason, Mathematics is viewed as if it were an inviolable structure where a general statement such as "using numbers" is the most basic pattern to be derived. When a predominant usage of dichotomies is pointed out, a reflexive system of rationalization takes hold of those who may have unknowingly placed Mathematics an a pedestal... and like a god, any presumed blemish is dismissed and turned into a form of self-representative ignorance on the part of those making a given inquiry. For example, a person questioning god might then turn to questioning their faith as being unworthy of an answer, and that a lack of reply either means one is not smart enough to interpret the "message", or one is not asking an appropriate question in an appropriate way. Far too many are refusing to subject Mathematics to the same scrutiny they commonly do with other activities. Because Mathematics is thought to be a tool aiding in the identification of basic patterns, the tool itself is not being looked at in order to uncover its basic patterns, because Mathematics is a poor tool for analyzing itself. Mathematics is biased towards itself. Mathematics is a vernacular of human cognition, it is a coded representation humanity has not yet learn how to fully decode.
While Mathematics may or may not be a "common tongue" used by all sentient beings, let us not overlook the possibility that its commonality may be similar to expressions like the babbling of infants. The Mathematics used by humans may be a fore-runner to the "mathematical speech" that is achievable, just as babbling precedes greater articulation and an enlarged vocabulary. Whereas some view the state of Mathematics as some wondrous level of cognitive expression, I am inclined to think of it in terms of being a primitive level of communication. And like many primitive languages, some level of social viability is acquired where certain gestures coupled to certain contexts can be alternatively viewed as being more serious, more complex, more important, though the basic structure of the language employed in all contexts is, for-the-most-part, unchanged and viewed in terms of attached emphasis. Indeed, let us wonder at what level of cognitive development humanity presently reigns at when compared to the supposed existence of superior intellects existing elsewhere. At what level of cognitive expression do we rate human Mathematics? At a pre-babbling stage of development? A Babbling stage? A first word, second word or beginning sentence structure, though it provides immense utility for those practiced in the craft of this type of articulation? Much like the made-up languages (idioms, abbreviations, etc...) indulged in by some teenagers (Pig Latin & Other Made-Up Languages by Lara Henerson, Jan. 25th, 2022), as well as movie script writers and known as: (Idioglossia. No less, I recall taking a test as a teenager for the military O.C.S. (Officers Candidate School) in which I encountered a given portion of the test in which one had to memorize a made up (gibberish) language and use it to complete a section of the overall testing required. In other words, made-up languages are not few and far between, but are an active process of socialization amongst individuals and groups where conflicts arise because multiple languages may attempt to secure a dominant position such as the language of verbalization, dress, hand gesture, context, subject, etc... For example, two or more groups may look human and speak the same Language such as Chinese, but view each other differently due to the "language" of personal names, gender, birthplace, age, occupation, etc...
Whereas many may claim that Mathematics is a universal language understood by all sentient beings who might want to communicate on some common ground, the Mathematics of humanity may be on the level of babbling or some "first word/first step" activity; whereby a sentient being whose mathematics is at a more developed level of articulation may not be able to convey any greater level of knowledge beyond a nursery level; and are thus limited in the manner they can interact with humans, other than repeating simple articulations so as to be recognized by humans as (presumably) understanding them and have a willingness to communicate. One such articulation may well be a binary code, and this includes the binary code existing in the fundamental structure of Mathematics, as well as the colloquial attention given to the old Yin/Yang idea of pairing (and presumed complementarity). Using geometries such as Crop Circles as a form of communication is much too sophisticated for most humans, though in terms of expression, may be thought of by an extra-terrestrial as a very basic form of using pictures as a show-and-tell model of interaction. Because far too many people view the current state of Mathematics as an expression of some advanced thinking, the idea that it may be little more than a simpleton's lineup of stick figures prevents humanity from looking elsewhere as to a greater level of thought processing to be achieved. Like a primitive who takes a flame from a burning twigs after a lightning strike and learns to use it for cooking, protection, warmth and extending day-light activities; current Mathematics may be such an activity that has not yet been developed as a mechanism to be produced alternatively by way of some fire-starting technique, much less by way of a developed match, lighter or even magnifying glass.
However, this being said, and let us for the sake of argument agree with the idea that current Mathematics is at a present primitive level of development; how then do we proceed to a more advanced stage, if all presumed advanced stages persist in the usage of a basic binary thought process? Analogously, whereas we think computer languages have developed a great sophistication by the addition of a trinary Boolean logic, just as the pairing of amino acids has the addition of a triplet code; are we not limited by the underlying two-patterned (binary) structure, and use the after-math complexities as feathers in our cap to be worn proudly without question? Just as we seek creating a trinary (ternary) computer, and biology (perhaps) is seeking to create a trinary biology (despite its present experimentations creating Triploidy (triploidic mutations as an expression whereby biology tests the "waters" of the prevailing environment awaiting more favorable conditions where triple chromosome expressions will be able to evolve into greater viability); is it possible to create a Mathematics whose fundamental structure also is trinary as opposed to its present binary format... particularly when researchers are not recognizing the similarity of patterning amongst different subjects and (in addition) relating this to developmental biology involving incrementally deteriorating environmental influences (pressures) affecting mental activity? It is almost unreasonable to expect Mathematics to evolve to a greater level of design if the current social structure of Mathematical training is practiced like a Medieval Guild that is accepted as an expected standard of mentally focused socialization, whereby the idea of "something better" is greatly obscured by an aligned system of enterprises providing a financial income. No less, if we include all diversions of thought (music, literature, dance, art, etc...) as other types of primitive thinking, how does one suggest the existence of a greater type of thinking if all philosophical gestures about this come to articulate some sort of artificiality where speed is introduced as a means of identification, though it necessarily incorporates multiple views from the old ideas and repackages them in terms and contexts such as in Artificial Intelligence focused on mimicking human activity, though at an increased speed— as a definition of greater intelligence?
Is someone smarter because they can multi-task or speak multiple languages or run faster, jump higher with or without a connection to some desired tradeable product such as money, land, weapons or other resource? Indeed, how would we define a greater level of intelligence if the standard of identification is based primarily on what a given person deems to be an expression of that which they can or would like to be able to do?
While the idea that meaning can be "lost in translation", it is not common for topics of conversations to suggest that Mathematics not only is a made-up language, but has become adopted as being viewed as a Universal language (like an Omnipresent god-figure) to which institutionalized monuments have been erected and enforced as the "One, True, Absolute" model of thought and anyone who wants to achieve enlightened perspectives from the vantage point of a given subject— must learn or be viewed as some type of country bumpkin or hillbilly or uneducated vagrant pretending to be more sophisticated in thought than they are; due to a lack of Mathematic's language usage.
Otherwise noted (at least in science fiction movie scripts) as a Universal Language, and often associated with the binary language of computers, it is of need to question such a view since the binary in computers and the largely unrecognized duality structure of Mathematical thinking, may be the product of human physiology such as the two-patterned repetitions of the human gait, the bilateral body structure, and multiple two-patterned structures in human biology (such as the double helix of the DNA molecule). It is rather arrogant for humans to consider themselves as practicing some basic usage of advanced thought processing consistent with all types of intelligence... an in particular, those which may far exceed our present state of existence. The use of a binary formula may be the result of some environmentally influenced, biologically driven imperative that is not shared by other life forms, and would therefore only communicate in a binary or dualistic model of symbolic thinking because the more readily see how the human species adheres to a pattern of cognitive thinking closely aligned with it biology with a developmental sequencing that can be enumerated into a serial recognition in-tune with the idea of progress, as an amplification of that which we have come to designate as ego termed Evolution in the context of biology and infinity in the context of a number line to indicate a believed-in view consistent with the notion that complexity is to be equated with advancement.
Whereas the Yin/Yang collection of two-patterned examples can be viewed as a rudimentary means of pairing into sets-of-two (like a computer's zero/one sets-of-two pairing with an off/on electrical switch); it also represents an illustration of early cognitive processes which can be equated with a primitive counting system that reveals the value of "1" and "2" placed together, but the notion of a larger enumeration came in the form of an embellishment called the I-Ching triads... which are actually Biads masquerading as triads. The I-Ching is an example of an early manifestation of human cognitive activity trying to exceed its grasp of number (quantity) by way of doubling, just as we see in early historical records of counting systems. An act of practicing a type of counting system (such as present efforts involving homelessness), is a means by which some method of equation can be adopted and thus used as a presumed means of addressing one or more problems... though the root cause or origination is not seen, nor does the idea of transition (where punctuated and throwback developmental scenarios may occur).
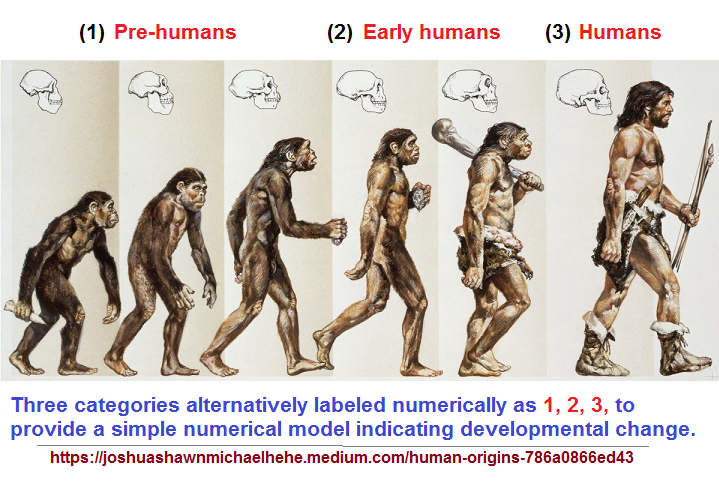
In a general evolutionary sense, one might say that humans came third, the supposed "missing link(s)" came second, and primates came first. Despite a chart which illustrates multiple humanoid forms characteristically seen similar to the following image, we can describe human evolution in a pattern-of-three, which provides an easy means of understanding the values of "1- 2- 3" as representing progress. Alternatively we might describe the hominid line of descent as 1) pre-human, 2) early human, 3) human as 3 generalized categories. The idea of transitioning from one stage to the next is easily grasped, whether or not you believe in evolution.
- Observation... discovering how to acknowledge opposites
- Problem solving... Convergent versus Divergent thinking
- Language... use of words to describe observations
- One-to-One Correspondences... pairing, combining
- Number sense... typically paired by way of analogy
- Shapes recognition... pointy objects/non-pointy surfaces (flat, round)
- Spatial sense... in/out, small/large, up/down, etc...
- Sets and Classification
- Ordering/Seriation
- Comparing
- Patterns... similarity/difference
- Counting... 2 types/models (of conscious counting, "subtizing" may be viewed as unconscious, instinctual or an "intuitive sizing" ability where
actual enumeration is not taking place):
- Rote counting- reciting numbers in order from memory.
- Rational Counting- counting items in a group and then understanding that the last number stated IS the amount for the set.
- Intentional Measurement (Calculus by way of conscious counting) versus Subtizing Measurement (let us say instinctive, intuitive, unconscious measurement)
- Measurement... differences aligned with some notion of opposition or stark contrast (large/small, fast/slow, up/down, etc...)
- Parts and Wholes
- Numbers and Symbols (pairing)
- Graphing... (X and Y axis elements is typical arrangement)
Sometimes shown as collated ideas referencing opposites or pairs or called dichotomies, dualities, hermaphroditic, bifurcation, dyad, etc... Yet nonetheless to be viewed as one might suggest sets-of-two. The two-patterned cognitive pattern persists just like we see a persistence of dichotomies in the instruction of psychology: Persistent Dichotomies page 1. The problem with correlating the "twos" in Mathematics with the "twos" in the Yin/Yang philosophy is that it is typical for the researcher to stop at this juncture of realization. They do not then proceed to add additional patterns-of-two ideas found in other subjects, but the few who may do so, eventually reach a point in their documentation where they come to think that there are so many examples, it is either futile or too exhausting to continue looking at the "two" in context with other patterns to pay witness to the presence of the "two" in the midst of a sequence such as "1-2-3". Such a researcher may be inclined to make excuses for the absence of a dominant pattern-of-two and act in a dismissive way towards other patterns because their previous two-patterned orientation is not flexible enough to be enlarged into a larger appreciation of the pattern with other patterns, nor enabled to make themselves take on the part of playing the Devil's advocate in stating similarly as I have done when it comes to the absence of a three pattern... namely, if patterns-of-two are so important and so dominant, then why are there instances not only of absence, but as a component of a larger set?
Before continuing it is of need to point out that different types of Mathematicians exist, even if you might not want to include pedestrian types of Numerologists, Astrologers, Gamblers, and Accountants as Mathematicians. You may prefer to include only those who engage in the types of mathematical models taught in school and none of the ideas once practiced widely (or used more widely) in ancient times prior to the advent of presumed "serious' mathematics beyond basic Arithmetic such as Geometry, Trigonometry, Algebra and Calculus; even if early civilizations viewed their rudimentary forms of mathematics in a very serious way, with or without a religious or other cosmogonic- based association to infer a greater magnitude of importance. Indeed, just as we see different representations of ability addressed by terms seen in sociology and everyday colloquial encounters such as novice, shade tree mechanic, journeyman, apprentice, newbie, master, skilled, professional, beginner, (also: lower- middle- upper), inferior, superior, specialist, partitioner, tinkerer, educator, dabbler, mad scientist, forager, student, experimenter, inventor, etc., we see the same types of thinking contours when different people are engaged with mathematics. Whereas some prefer to see themselves in the manner of a skilled artisan engaged in top levels of Chess play, others routinely use mathematics as if playing some other game whose rules and parameters of play may not be as strict, but they consider to be more fun and forgiving so that multiple types of people may play and be entertained or think themselves having achieved some measure of dominance over others.
My interest in the "threes phenomena" led me towards accepting that the "three" pattern takes on several forms and formulas but that there were several occasions in which another pattern apparently dominated. In fact, in playing the part of the Devil's Advocate in my research on the Threes Phenomena, I had to question the validity of the importance of the "three" when other patterns came to dominate in several instances... meaning the "three" may not be as important (in all instances) as a collector of "threes" might want to assume in support of their efforts... but why is this the case? Necessarily so, it required expanding my knowledge base of occurrences from which probabilities might arise in accordance with an equation I had not previously appreciated to its fullest extent. For example, there are multiple composite situations involving patterns-of-three, one of which is the presence of patterns-of-two, and that I became suspicious as to the presence (or at least the observation) of patterns-of-three which emphasized a pattern-of-two such as the Major Premise- Minor Premise/ Conclusion. Whereas three references were sighted, two of them were a polarity. Hence, the idea of an "embellished" dichotomy seemed an appropriate way of describing the situation as well as noting (by including ideas from developmental biology), that a "two" often represented a transitional stage to a larger set, such as in the case of three Germ layers in Development and Organogenesis (development of the body and organs).
It was especially important to see that with respect to two germ layers, there exists life forms sometimes referred to as Diploblasts, meaning that a "pattern-of-two" was an important stage of development preceding patterns-of-three, or those life forms called Triploblasts. Such a concurrent existence meant that there could be a dominant "pattern-of-two" presence amidst a dominant pattern-of-three, and that I should neither overlook that such stages of development most likely arose from a singularity, even if there were not a list of "Monoploblasts" with which to exert one's perusal of this consideration. The idea of a 1 - 2 - 3 maturational development sequence is not too difficult to think of, though some readers may have some difficulty in transferring this idea to the topic of Mathematics, whereby they do not see the recurrence and dominance of patterns-of-two as a stage of development in Mathematics which exhibits multiple "life forms" (different types of Mathematics which use a pattern-of-two structural platform), and that the possibility of a different species of Mathematics may already exist as a fledgling growth that is being overshadowed by larger two-patterned growth expressions in current Mathematics endeavors. If the analogy is sound and has some measure of validity... indicating the human brain has the capacity to evolve beyond its present usage of Mathematics, how do we go about letting it grow as well as nurturing it further, unless we are willing to transplant it to a more favorable environment or remove the strangling hold of roots and vines occurring with present day Mathematics? Indeed, can we force Mathematics to evolve as one might think about artificially terra-forming a planet and evading the drums of opposition, detour and oppressive confinement by an institutionalized practice of indentured servitude enforced by commerce, government and religion?

Along with the ability to learn basic concepts which exhibit a basic repetition of cognitive construction themselves; we need to include the basic types of memorization in order to pay witness to the use of ideas representing opposites by way of different labeling, and are sometimes referenced in terms of functionality such as "encoding, storing, and retrieving", which brings to mind the three basic Boolean operators labeled "And, Or, Not":
- short=term memory/long-tern memory
- working memory/ (I call "non-working" memory as 'storage memory' though this item is not routinely brought up unless one is speaking of computers)
- sensory memory (One might also call this fleeting, momentary or episodic memory depending on context and what is being compared to it)/ extra-sensory memory which can be viewed in terms of repeating a memory as if in a loop... let us say like a song or music or some other sound (which one might describe metaphorically as different types of "voices") that sticks in one's mind for awhile.
- primary (working)/secondary (storage)
- explicit memory (conscious retrieval)/ implicit memory (unconscious retrieval) (Neuro-anatomical, Neuro-physiological and Psychological Basis of Memory:)... H.O.B. Note: notice that the authors did not combine the word "Psychological" with "Neuro" to produce "Neuropsychological", though in the present context the term would be valid.
- physical memory/spiritual memory??? (In other words, can memory be described as having the forms of "Body- Mind- Soul"?)
- physical memory/emotional memory??? (Different forms of memory or different contexts of memory retrieval?)
- male memory/female memory??? (Are there underlying different patterns to be viewed, though vocabulary restricts our ability to recognize them?)
- human memory/non-human memory
- declarative and non-declarative
- associative/dissociative
- good/bad
- instructive/destructive
- common memory/compensational memory (for example: If one loses their sight, one or more other senses may increase their range and sensitivity as a compensation)
- semantic memory (long-term conscious memory)/ short-term non-vocal or sub-vocal memory
- non-verbal memory (you remember something but keep it to yourself)/ verbal memory is recall and voicing the memory
- Involuntary and Voluntary Memory (remembering something intentionally or not)
- Prospective and Retrospective Memory (Prospective refers to memory of events, appointments, things to come, while retrospective memory relates to the past... which may incline some readers to think in terms of "Mean- Median- Mode", though they all apply to a centralized tendency; yet invite the idea of a needed third element between these two types of memory)
- Sensory Modality-Specific Memory (Sensory modality-specific memory has to do with the recalling of information with a sensory stimulus)... and its opposite might be termed a memory event which occurs as a "Eureka!" or spontaneous realization which becomes expressed in the way and means a person is practiced in. For example, the medium of a painter will be different from that of a Mathematician or a cook or a carpenter, etc...
Interestingly, despite the different labels one might encounter in describing types of memory, it is not difficult to point out the use of dichotomies in describing them. In fact, if one subscribes to the view that there are three basic types labeled as Short-term, Long-term and Sensory; it is not difficult to see that this three-patterned collation is an embellished dichotomy similar to the basic structure of a syllogism labeled as Major premise, Minor premise, Conclusion. Though the words differ and the application is context specific, the underlying cognitive structure of these ideas is similar, because both reference an internal dichotomy with a supposed secondary single:
- Short-term/ Long-term... Sensory
- Major premise/ Minor premise... Conclusion

Clearly, both are of a similar underlying (dual) cognitive structure which repeats itself, (to which we might well add other examples of this cognitive structure formula) just as we see multiple cognitive repetitions occurring in Mathematics. While each of the examples is defined as a "three", one must ask if this is an unrecognized evolutionary exercise of the brain to stretch beyond it currency of "twoness" by introducing a perspective designed in such a way that one is fooled into thinking they have achieved an actual "three" activity, though a "three" perception may exist but not the means by which an actual three-pattern structure has been developed beyond linguistic suppositions which act as tongue twisters much in the manner the rock-paper-scissor game frequently uses three players that use the tool of two hands. Hence, like an insect, we see three pairs (of hands instead of legs) and the tripod 'gait' of insects plays out in the cognitive 'gait' of varying human explorations. Because of the closed (but variable) environment to which all life exists, it is not unrealistic for us to find similar parts, processes and functionalities occurring in different life forms, despite researchers use of different vocabularies in describing an entire species with labels meant to illustrate something special, something unique, something not seen nor described before... as if such activity is a projected expression of what they want to believe exists within themselves.
Date of Origination: 24th August 2022... 4:07 AM
Date of Initial Posting: 2nd September 2022... 6:31 AM
Updated Posting: 2nd January 2023... 11:03 AM